Ejemplos de preguntas sobre algoritmos | Recurrencias | conjunto 2

julio 5, 2022 Rudeus Greyrat

Pregunta 1: ¿Cuál es la complejidad de T(n)?
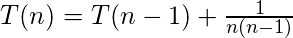
1. Θ( ¹ ⁄ _norte )
2. Θ( ¹ ⁄ _{norte ²} )
3. Θ( 1 )
4. Θ( ln( n ) )
Respuesta: 3
Explicación: Usando la técnica de sustitución para resolver la función recursiva dada, la forma cerrada (forma no recursiva) de T(n) se puede adivinar inductivamente de la siguiente manera: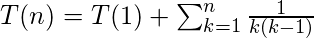

$T(n) = T(1) + \sum_{k=1}^{n} \frac{1}{k(k-1)}$

Antes de ir más lejos e involucrarnos en fracciones complicadas, sería mejor simplificar la ecuación en cuestión. El método de descomposición en fracciones parciales es un método común para expresar una fracción racional, donde tanto el numerador como el denominador son de forma polinomial, como una suma de una o varias fracciones con un denominador más simple. El uso de este método da:

$\frac{1}{k(k-1)} = \frac{A}{K} + \frac{B}{k-1}$

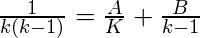
Haciendo esta descomposición, los valores de A y B se encontrarían como -1 y +1, respectivamente. Al realizar esta descomposición, la forma no recursiva de T(n) se escribirá como:

$T(n) = T(1) + \sum_{k=1}^{n} (\frac{1}{k-1} - \frac{1}{k})$

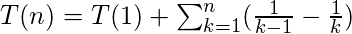
Ampliar esta representación compacta de T(n) dará como resultado:

$T(n)=T(1)+((\frac{1}{1}-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+...$

$+(\frac{1}{n-2}-\frac{1}{n-1})+(\frac{1}{n-1}+\frac{1}{n}))$

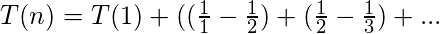
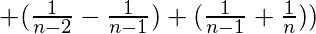
Como será evidente, cada fracción, excepto la primera y la última, se presenta dos veces, pero cada vez con signo contrario; entonces, todas las fracciones se desvanecerán excepto la primera y la última:

$T(n) = T(1) + \frac{1}{1} - \frac{1}{n} = T(1) + 1 - \frac{1}{n}$

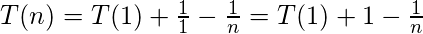
De la última ecuación que se acaba de derivar, la complejidad asintótica de T(n) es:

$T(n) \in \theta (1 - \frac{1}{n}) \in \theta (1)$
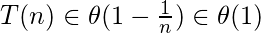
Pregunta 2: ¿Determinar (contar) el número total posible de strings de longitud N con cuatro caracteres {a, b, c, d} que contienen un número par de «a»? [C(N) es la abreviatura de la función Count(N) para cumplir este propósito.]
1. C(N) = 5,0 * 3 ^N-1 – 1,0 * 5 ^N-1
2. C(N) = 1,0 * 4 ^N + 6
3. C(N) = 0,5 * 2 ^N + 0,5 * 4 ^N
4. C(N) = 1,0 * 2 ^N + 2,0*(3) ^N
```
Example: 

For n = 1, there are 3 distinct strings: C(3) = 3
```
- b, c, d.
Para n = 2, r, para n = 2, 10 strings posibles son: C(10) = 10
- aa, cama y desayuno, cc, dd, antes de cristo, bd, cb, discos compactos, db, corriente continua
Respuesta: 3
Explicación: Hay dos escenarios posibles para el primer carácter de las strings con la restricción dada:
1. El primer carácter puede ser uno de los posibles caracteres «b», «c» o «d», excepto «a». En este caso, el objetivo es encontrar el número de strings de longitud restante «N-1» que están formadas por un número par de «a» s.
  - C(N) = 3* C(N-1)
2. El primer carácter puede ser «a», y uno de los «a» ya se ha producido; por lo tanto, se debe contar el número de strings posibles con números impares de «a». Este número no se puede llamar C(N-1), pero C(n) todavía se puede lograr usando C(N-1).
  - C(N) = 4 ^N-1 – C(N-1), donde:
    - 4 ^N-1 : número total de posibles strings de longitud (N-1) con cuatro caracteres
    - C(N-1): número de strings de longitud (N-1) formadas por un número par de “a”.
Como los dos escenarios distintos mencionados anteriormente no pueden ocurrir al mismo tiempo, el número total de strings es la suma de los casos:

$C(N) = 3 * C(N-1) + (4^{N-1} - C(N-1))$

$= 2*C(N-1) + 4^{N-1}$

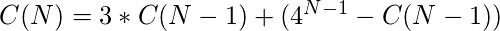
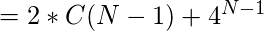
Se necesitan dos condiciones iniciales como las que se exponen a continuación para encontrar una solución particular:
1. Para n = 1, hay 3 strings distintas: b, c, d.
2. O, para n = 2, 10 strings posibles son: aa, bb, cc, dd, bc, bd, cb, cd, db, dc
Ahora bien, el problema se puede formular como:

$C(N) = C_{1} * 2^{N} + C_{2} * 4^{N}, C(1) = 3, C(2) = 10$

El número total posible de strings con la restricción dada es:

$C(N) = 0.5 * 2^{N} + 0.5 * 4^{N}$
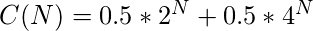
Pregunta 3: ¿Cuál de las funciones de recurrencia no tiene solución de forma polinomial?
1. $T(N) = 2 * T(n-2) + 1$
2. $T(N) = T(n-1) + N^{2}$
3. $T(N) = T([ \frac{8}{9} n ] ) + 9 * n + 1$
4. $T(N) = 100 * T(\frac{n}{99}) + N$
Respuesta: 1
Explicación: Se requiere la solución de todas las ecuaciones anteriores para ver la solución a qué opción no es polinomial. Se verá que todas las soluciones son de forma polinomial, excepto la que se trae en primera opción. Aquí están los análisis de las opciones:
1. La opción (1) tiene solución exponencial: Para encontrar la solución homogénea de la ecuación presentada en la primera opción, se requiere de las raíces de su ecuación característica:
  $T(N) = 2 * T(n-1) + 1 \Rightarrow r^{2} - 2 = 0 \Rightarrow r = \pm \sqrt{2}$
  
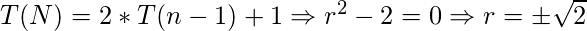
  Por lo tanto, la solución es de forma exponencial:
  
  $T(n)= c_{1} *( \sqrt{2})^{n}+ c_{2}*(-\sqrt{2})^{n}$
  
  $= c_{1} *2^{n/2}+c_{2} *(-1)^{n} * (2)^{n/2}$
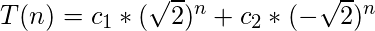
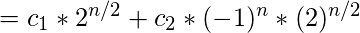
2. Opción (2): La ecuación de la segunda opción se puede resolver fácilmente mediante la técnica de sustitución:
  $T(n) = T(n-1) + n^{2} = T(n-2) + n^{2} + (n-1)^{2}$
  
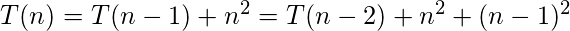
  La forma cerrada de T(n) que se puede adivinar inductivamente es:
  
  $T(n) = T(1) + \sum_{k=1}^{n} k^{2}$
  
  $= T(1) + sum.of.square.numbers \approx \frac{n(n+1)(2n+1)}{6}$
  
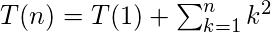
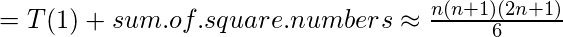
  Esto dice que es una función polinomial de tercer grado (polinomio cúbico):
  
  $T(n) \in \theta (T(1)) + \theta ( n^{3} ) \in \theta (1) + \theta (n^{3}) \in \theta (n^{3})$
3. Opción (3): De acuerdo al teorema maestro , la complejidad de la ecuación propuesta en la tercera opción es de $\theta(n)$ .
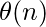4. Opción (4): La ecuación de la cuarta opción se encuentra en el caso 3 del teorema maestro ; por lo tanto su complejidad es de $\theta(n^{\frac{100}{99}})$ .
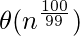Pregunta 4: ¿cuál da la mejor estimación de la complejidad asintótica de F(n)?
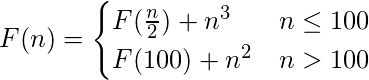
1. O( n ³ )
2. Ω( n ² )
3. O( n ² )
4. Θ( norte ² )
Respuesta: 4
Explicación: Hay algunos hechos difíciles a considerar antes de tomar cualquier decisión en estos problemas:
1. La mejor estimación asintótica es cuando el comportamiento de la complejidad se expresa mediante la notación Θ. Esto se basa principalmente en el rendimiento promedio de los algoritmos, el llamado escenario de caso promedio, que necesita un análisis complicado que los programadores prefieren usar otras notaciones como O(); sin embargo, sigue siendo una buena práctica tratar de encontrar el límite más estrecho posible.
2. Las notaciones asintóticas matemáticas delinean el comportamiento de las funciones de complejidad en el infinito, o cuando “n” tiende a una cantidad muy grande. El infinito es un concepto hipotético y abstracto que no se puede alcanzar en la vida real. A los efectos de los cálculos, y para tener una idea del comportamiento de una función, el número que se debe considerar depende únicamente del problema. En este problema parece no haber límite en el tamaño de los datos de entrada «n».
3. Para deshacerse de las posibles trampas proporcionadas por los fabricantes de pruebas, se debe asignar un valor suficientemente grande a n; en este problema no se elegirán valores pequeños como 100 o 1000. Como existe la necesidad de comparar la complejidad de n ³ para n < 100, versus n ² para n > 100, los valores superiores a 1000 son aceptables, lo que hace que n ² supere a n ³ para n = 100. Incluso si estuviéramos a punto de volver a calcular F(100) en cada llamada, para n> 1000, n ² siempre es mayor que F(100) que es del orden de n ³ para valores pequeños como n=100. El valor de F(100) puede simplemente ignorarse en los cálculos requeridos para n > 1000.
4. En este problema, sería una gran idea usar un espacio de memoria auxiliar de Θ(1) para guardar el resultado de F(100) de inmediato para uso futuro, sin tener que volver a calcular F(100) en cada llamada para n >100. Entonces, la complejidad de F(100) sería de O(1), quizás solo para leer un valor, y la complejidad de F(n) sería de Θ(n ² ) para n>100.
La complejidad de F(n) es:

$F(n) \in \Theta (n^{2})$
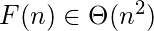
Pregunta 5: ¿Cuál especifica rangos apropiados para k y α (alfa), donde se cumple la siguiente expresión asintótica?
```
  
```
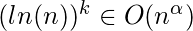
1. α ≥ 0 y k ≤ α
2. α ≥ 0,1 y k ≥ 0
3. α > 1 & k ∈ R
4. α > 0 & k ∈ R
Respuesta: 4
Explicación: Hay una solución efectiva para este problema de un recurso muy confiable, una hoja de trucos de la universidad MIT . Sin embargo, no toda, pero una parte importante de la descripción presentada en esta solución se basa en las derivaciones que se pueden encontrar en esta hoja de trucos del MIT.

El objetivo es encontrar el rango en el que la expresión ln ^k n ∈ O(n ^α ) es cierto. La peor condición bajo la cual esta expresión podría no ser mantenida es cuando se deja que el lado izquierdo de la expresión crezca mucho, mientras se intenta forzar que el lado derecho permanezca lo más pequeño posible; en otras palabras, intentar asignar un valor posible grande al exponente «k», mientras especifica valores muy pequeños para el exponente «Alfa» en el otro lado. Se pueden asignar valores pequeños, incluso menores que 1, a α. Sin embargo, por ahora, a α se le atribuye una constante específica opcional E, pero aún no un valor negativo; Α tampoco establece una variable E(n) que es una función de «n», ya que será un problema completamente nuevo para abordar, no el problema descrito en esta pregunta.

Sea α = |E| (una pequeña constante positiva opcional) y k>0; el objetivo es ver si la expresión ln ^k n ∈ O(n ^E ) es cierto, o no:

$\lim_{n \rightarrow \infty } \frac{ln(n)^{k}}{n^{| E |}} = (\lim_{n \rightarrow \infty } \frac{ln(n)}{n^{\frac{| E |}{k}}})^{k} = (\frac{ \infty }{ \infty })^{k}$

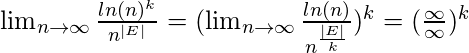
Aplicando la regla de Hopital se obtiene:

$(\lim_{n \rightarrow \infty } \frac{ln(n)}{n^{\frac{| E |}{k}}})^{k} = (\lim_{n \rightarrow \infty } \frac{\frac{1}{n}}{\frac{|E|}{k} * n^{\frac{|E|}{k}}-1})^{k}$

$= (\lim_{n \rightarrow \infty } \frac{\frac{1}{n}}{\frac{|E|}{k} * n^{\frac{| E |}{k}}* \frac{1}{n}})^{k} = (\lim_{n \rightarrow \infty } \frac{1}{\frac{|E|}{k} * n^{\frac{| E |}{k}} })^{k} = 0$

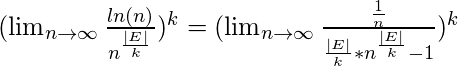
Lo que se deduce hasta ahora dice que no hay un exponente positivo “k” para una función logarítmica que pueda superar la variable “n” incluso con exponentes positivos muy pequeños. Seguro que lo mismo es cierto cuando las funciones logarítmicas toman exponentes negativos y se vuelven aún más pequeñas. En otras palabras:

$(ln(n))^{-|k|} \leq (ln(n))^{k} \in O(n^{|E|})$

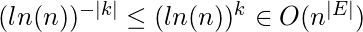
¿Qué pasa si el exponente Alfa toma valores negativos ( α = -|E| )? Como los exponentes negativos significan voltear las fracciones, y voltear las facciones se acompaña de cambiar el signo de desigualdad, se obtiene:

$\frac{1}{(ln(n))^{k}} \geq \frac{1}{n^{|E|}}$

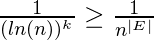
La notación O ya no se mantiene. Por tanto, el rango en el que se conserva la mencionada desigualdad es cuando k ∈ R & α>0; En lenguaje matemático:

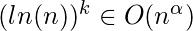$(ln(n))^{k} \in O(n^{\alpha} )$ para k ∈ R & α>0

Las expresiones polinómicas no pueden contener variables con exponentes fraccionarios; por lo tanto, este problema es aún más inclusivo ya que toma tales valores fraccionarios. Como resultado, este enunciado del problema describe con qué facilidad las expresiones polinómicas crecen más rápido que las funciones logarítmicas.

Fuente:
1. Hoja de referencia asintótica del MIT
2. Una compilación de exámenes universitarios de Irán (con un poco de resumen, modificación y también traducción)

Publicación traducida automáticamente

Artículo escrito por j*g*1991 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta