Cuadrado más grande que se puede formar usando bloques rectangulares dados

Dada una array arr[] de enteros positivos donde cada elemento de la array representa la longitud de los bloques rectangulares. La tarea es encontrar la mayor longitud del cuadrado que se puede formar usando los bloques rectangulares.

Ejemplos:  

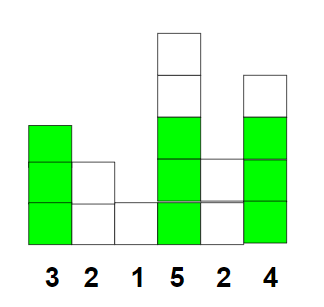
Entrada: arr[] = {3, 2, 1, 5, 2, 4} 
Salida: 3 
Explicación: 
Usando un bloque rectangular de longitud 3, 5 y 4, se puede construir un cuadrado de lado 3 como se muestra a continuación: 
 

Entrada: arr[] = {1, 2, 3} 
Salida: 2 

Acercarse:  

1. Ordena la array dada en orden decreciente.
2. Inicialice la longitud lateral máxima (digamos maxLength ) como 0.
3. Recorra la array arr[] y si arr[i] > maxLength entonces incremente maxLength y verifique esta condición para la próxima iteración.
4. Si la condición anterior no satisface, rompa el ciclo e imprima maxLength .

A continuación se muestra la implementación del enfoque anterior: 

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to find maximum side
// length of square
void maxSide(int a[], int n)
{
    int sideLength = 0;
 
    // Sort array in asc order
    sort(a, a + n);
 
    // Traverse array in desc order
    for (int i = n - 1; i >= 0; i--) {
 
        if (a[i] > sideLength) {
            sideLength++;
        }
        else {
            break;
        }
    }
    cout << sideLength << endl;
}
 
// Driver Code
int main()
{
    int N = 6;
 
    // Given array arr[]
    int arr[] = { 3, 2, 1, 5, 2, 4 };
 
    // Function Call
    maxSide(arr, N);
    return 0;
}

// Java program for the above approach
import java.util.Arrays;
 
class GFG{
     
// Function to find maximum side
// length of square
static void maxSide(int a[], int n)
{
    int sideLength = 0;
 
    // Sort array in asc order
    Arrays.sort(a);
 
    // Traverse array in desc order
    for(int i = n - 1; i >= 0; i--)
    {
       if (a[i] > sideLength)
       {
           sideLength++;
       }
       else
       {
           break;
       }
    }
    System.out.println(sideLength);
}
     
// Driver code
public static void main (String[] args)
{
    int N = 6;
 
    // Given array arr[]
    int arr[] = new int[]{ 3, 2, 1,
                           5, 2, 4 };
     
    // Function Call
    maxSide(arr, N);
}
}
 
// This code is contributed by Pratima Pandey

# Python3 program for the above approach
 
# Function to find maximum side
# length of square
def maxSide(a, n):
 
    sideLength = 0
 
    # Sort array in asc order
    a.sort
 
    # Traverse array in desc order
    for i in range(n - 1, -1, -1):
        if (a[i] > sideLength):
            sideLength += 1
        else:
            break
             
    print(sideLength)
     
# Driver code
N = 6
 
# Given array arr[]
arr = [ 3, 2, 1, 5, 2, 4 ]
 
# Function Call
maxSide(arr, N)
 
# This code is contributed by divyeshrabadiya07

// C# program for the above approach
using System;
class GFG{
     
// Function to find maximum side
// length of square
static void maxSide(int []a, int n)
{
    int sideLength = 0;
 
    // Sort array in asc order
    Array.Sort(a);
 
    // Traverse array in desc order
    for(int i = n - 1; i >= 0; i--)
    {
        if (a[i] > sideLength)
        {
            sideLength++;
        }
        else
        {
            break;
        }
    }
    Console.Write(sideLength);
}
     
// Driver code
public static void Main()
{
    int N = 6;
 
    // Given array arr[]
    int []arr = new int[]{ 3, 2, 1,
                           5, 2, 4 };
     
    // Function Call
    maxSide(arr, N);
}
}
 
// This code is contributed by Code_Mech

<script>
// Javascript program for the above approach
    // Function to find maximum side
    // length of square
    function maxSide( a, n) {
        let sideLength = 0;
 
        // Sort array in asc order
        a.sort();
 
        // Traverse array in desc order
        for ( i = n - 1; i >= 0; i--) {
            if (a[i] > sideLength) {
                sideLength++;
            } else {
                break;
            }
        }
        document.write(sideLength);
    }
 
    // Driver code
      
        let N = 6;
 
        // Given array arr
        let arr = [3, 2, 1, 5, 2, 4 ];
 
        // Function Call
        maxSide(arr, N);
     
 
// This code contributed by aashish1995
</script>

3

Complejidad de tiempo: O(N*log N)  
Espacio auxiliar: O(1)