Método de eliminación de estado:
reglas para convertir un DFA/NFA//Ɛ-NFA en la expresión regular correspondiente.
El método de Arden no es capaz de convertir Ɛ-NFA. Mediante el método de eliminación de estado, puede encontrar RE de manera conveniente y rápida sin escribir nada solo con la imaginación.
Regla 1:
si no hay flancos entrantes al estado de inicio, continúe para verificar otras reglas. Si hay transiciones entrantes al estado inicial, para deshacerse de los bordes entrantes, haga un nuevo comienzo sin bordes entrantes y un borde saliente al estado de inicio anterior con transición Ɛ. el estado inicial anterior ahora es el estado normal con una transición Ɛ entrante adicional.
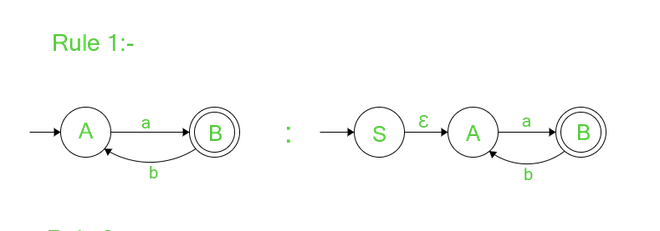
Regla 2:
si no hay bordes salientes desde el estado final, continúe para verificar la última regla. Si hay transiciones salientes desde el estado final, para deshacerse de los bordes salientes, cree un nuevo estado final sin bordes salientes y un borde entrante desde el estado final anterior de la transición Ɛ. El antiguo estado final se transforma en un estado normal con la transición añadida de Ɛ.
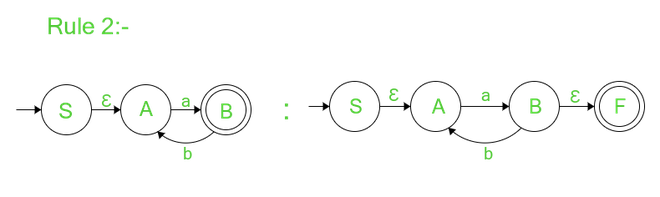
Regla-3:
Si no hay múltiples estados finales, proceda a la eliminación (excepto final e inicial) de los estados normales. Si los autómatas tienen múltiples estados finales, se recomienda eliminar su estado de ser estados finales y agregar una transición Ɛ saliente a un nuevo y único estado final sin transiciones salientes.
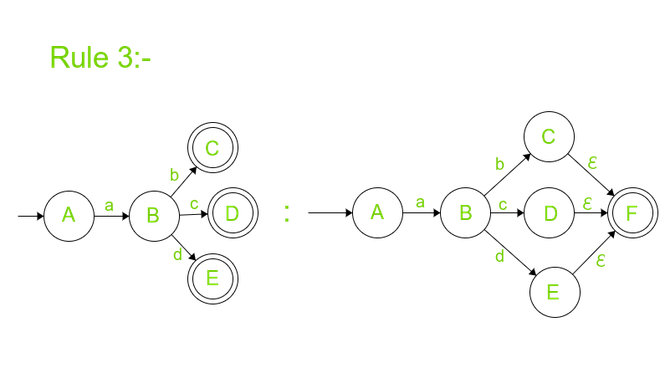
Eliminación de estados normales:
tomemos un ejemplo de DFA e intentemos encontrar RE mediante el método de eliminación de estados.

DFA que termina en ‘a’
Ahora se viola la Regla 1, 2 para satisfacerlos y crear un nuevo estado final y un nuevo estado inicial con una transición Ɛ entrante y una transición Ɛ saliente, respectivamente.
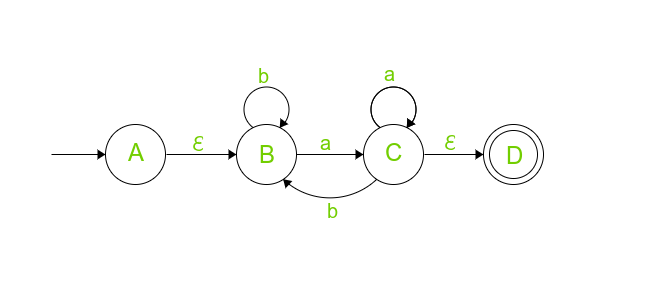
Elimine los estados B y C en el orden que desee, ya que la respuesta será la misma en ambos casos, ahora eliminemos B primero.
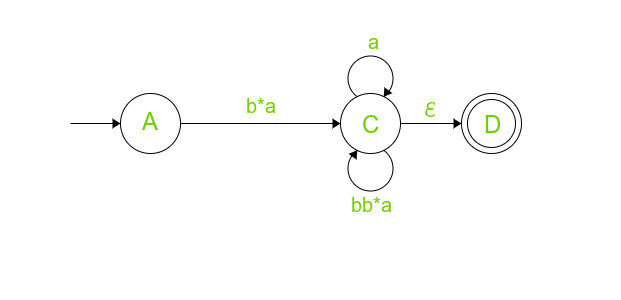
Elimine B e imagine que si no hubiera habido ningún estado B, entonces llegamos al estado C directamente desde el estado inicial A con el símbolo de entrada de ‘Ɛb*a’, podemos ignorar Ɛ, entonces el símbolo de entrada será ‘b*a’ de A a c
El borde saliente del estado C al B ahora se convierte en bucle automático ya que el estado B no está allí, compare las imágenes de arriba y abajo después de eliminar el estado B. Edge de C va a B, toma b * y regresa a C con ‘a’, esto puede suceder en un tiempo infinito, por lo tanto, el bucle automático de b (b) * a. Podemos los dos bucles automáticos ‘a’ y ‘bb*a’ como (bb*a +a), lo que significa que podemos atravesar un bucle a la vez. Ya sea a o bb*a como resultante (bb*a + a) es un cierre en el estado C = (bb*a + a)*.
Ahora, después de eliminar el estado C, llegaríamos al estado final D directamente desde el estado inicial A, ahora estábamos alcanzando el estado C mediante la entrada de ‘b*a’ en el estado C, estamos tomando bucles infinitos en (bb*a + a) y con Ɛ alcanzando el estado final D. Por lo tanto, finalmente no quedan estados normales, obtuvimos un flujo de símbolos de entrada directamente desde el inicial hasta el final, que es b*a(bb*a + a)*.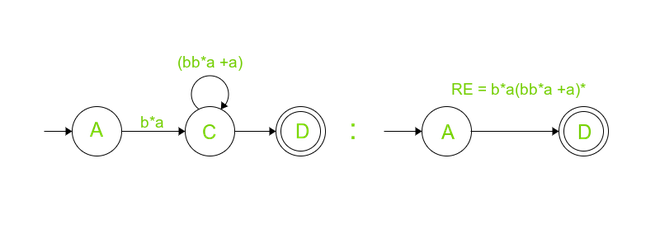
Si llegó hasta aquí, gracias por leer este artículo, este método lo ayuda a encontrar RE rápidamente. También ayudará a los aspirantes a GATE-CSIT ya los estudiantes universitarios de CS. Si entiende este Concepto, intente encontrar RE para los 0 pares y los 1 impares, una pregunta muy complicada. También publicaré un artículo al respecto. hazme ping si encuentras algún error.