El pequeño teorema de Fermat establece que si p es un número primo, entonces para cualquier número entero a, el número a p – a es un número entero múltiplo de p.
Aquí p es un número primo
a p ≡ a (mod p).
Caso especial: si a no es divisible por p, el pequeño teorema de Fermat es equivalente al enunciado de que a p-1 -1 es un múltiplo entero de p.
a p-1 ≡ 1 (mod p)
O
a p-1 % p = 1
Aquí a no es divisible por p.
Toma un ejemplo Cómo funciona el pequeño teorema de Fermat
Ejemplo 1:
P = an integer Prime number a = an integer which is not multiple of P Let a = 2 and P = 17 According to Fermat's little theorem 2 17 - 1 ≡ 1 mod(17) we got 65536 % 17 ≡ 1 that mean (65536-1) is an multiple of 17
Ejemplo 2:
Find the remainder when you divide 3^100,000 by 53.
Since, 53 is prime number we can apply fermat's little theorem here.
Therefore: 3^53-1 ≡ 1 (mod 53)
3^52 ≡ 1 (mod 53)
Trick: Raise both sides to a larger power so that it is close to 100,000.
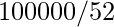 = Quotient = 1923 and remainder = 4.Multiplying both sides with 1923: (3^52)^1923 ≡ 1^1923 (mod 53) 3^99996 ≡ 1 (mod 53)Multiplying both sides with 3^4: 3^100,000 ≡ 3^4 (mod 53) 3^100,000 ≡ 81 (mod 53) 3^100,000 ≡ 28 (mod 53).Therefore, the remainder is 28 when you divide 3^100,000 by 53.
= Quotient = 1923 and remainder = 4.Multiplying both sides with 1923: (3^52)^1923 ≡ 1^1923 (mod 53) 3^99996 ≡ 1 (mod 53)Multiplying both sides with 3^4: 3^100,000 ≡ 3^4 (mod 53) 3^100,000 ≡ 81 (mod 53) 3^100,000 ≡ 28 (mod 53).Therefore, the remainder is 28 when you divide 3^100,000 by 53.
Uso del pequeño teorema de Fermat
Si sabemos que m es primo, también podemos usar el pequeño teorema de Fermat para encontrar el inverso.
am-1 ≡ 1 (mod m)
Si multiplicamos ambos lados por -1 , obtenemos
a-1 ≡ a m-2 (mod m)
A continuación se muestra la implementación de lo anterior:
C++
// C++ program to find modular inverse of a
// under modulo m using Fermat's little theorem.
// This program works only if m is prime.
#include <bits/stdc++.h>
using namespace std;
// To compute x raised to power y under modulo m
int power(int x, unsigned int y, unsigned int m);
// Function to find modular inverse of a under modulo m
// Assumption: m is prime
void modInverse(int a, int m)
{
if (__gcd(a, m) != 1)
cout << "Inverse doesn't exist";
else {
// If a and m are relatively prime, then
// modulo inverse is a^(m-2) mode m
cout << "Modular multiplicative inverse is "
<< power(a, m - 2, m);
}
}
// To compute x^y under modulo m
int power(int x, unsigned int y, unsigned int m)
{
if (y == 0)
return 1;
int p = power(x, y / 2, m) % m;
p = (p * p) % m;
return (y % 2 == 0) ? p : (x * p) % m;
}
// Driver Program
int main()
{
int a = 3, m = 11;
modInverse(a, m);
return 0;
}
Java
// Java program to find modular
// inverse of a under modulo m
// using Fermat's little theorem.
// This program works only if m is prime.
class GFG {
static int __gcd(int a, int b)
{
if (b == 0) {
return a;
}
else {
return __gcd(b, a % b);
}
}
// To compute x^y under modulo m
static int power(int x, int y, int m)
{
if (y == 0)
return 1;
int p = power(x, y / 2, m) % m;
p = (p * p) % m;
return (y % 2 == 0) ? p : (x * p) % m;
}
// Function to find modular
// inverse of a under modulo m
// Assumption: m is prime
static void modInverse(int a, int m)
{
if (__gcd(a, m) != 1)
System.out.print("Inverse doesn't exist");
else {
// If a and m are relatively prime, then
// modulo inverse is a^(m-2) mode m
System.out.print(
"Modular multiplicative inverse is "
+ power(a, m - 2, m));
}
}
// Driver code
public static void main(String[] args)
{
int a = 3, m = 11;
modInverse(a, m);
}
}
// This code is contributed by Anant Agarwal.
Python3
# Python program to find
# modular inverse of a
# under modulo m using
# Fermat's little theorem.
# This program works
# only if m is prime.
def __gcd(a, b):
if(b == 0):
return a
else:
return __gcd(b, a % b)
# To compute x^y under modulo m
def power(x, y, m):
if (y == 0):
return 1
p = power(x, y // 2, m) % m
p = (p * p) % m
return p if(y % 2 == 0) else (x * p) % m
# Function to find modular
# inverse of a under modulo m
# Assumption: m is prime
def modInverse(a, m):
if (__gcd(a, m) != 1):
print("Inverse doesn't exist")
else:
# If a and m are relatively prime, then
# modulo inverse is a^(m-2) mode m
print("Modular multiplicative inverse is ",
power(a, m - 2, m))
# Driver code
a = 3
m = 11
modInverse(a, m)
# This code is contributed
# by Anant Agarwal.
C#
// C# program to find modular
// inverse of a under modulo m
// using Fermat's little theorem.
// This program works only if m is prime.
using System;
class GFG {
static int __gcd(int a, int b)
{
if (b == 0) {
return a;
}
else {
return __gcd(b, a % b);
}
}
// To compute x^y under modulo m
static int power(int x, int y, int m)
{
if (y == 0)
return 1;
int p = power(x, y / 2, m) % m;
p = (p * p) % m;
return (y % 2 == 0) ? p : (x * p) % m;
}
// Function to find modular
// inverse of a under modulo m
// Assumption: m is prime
static void modInverse(int a, int m)
{
if (__gcd(a, m) != 1)
Console.WriteLine(
"Modular multiplicative inverse is "
+ power(a, m - 2, m));
else {
// If a and m are relatively prime, then
// modulo inverse is a^(m-2) mode m
Console.WriteLine(
"Modular multiplicative inverse is "
+ power(a, m - 2, m));
}
}
// Driver code
public static void Main()
{
int a = 3, m = 11;
modInverse(a, m);
}
}
// This code is contributed by vt_m.
PHP
<?php
// PHP program to find modular inverse of a
// under modulo m using Fermat's little theorem.
// This program works only if m is prime.
// To compute x raised to
// power y under modulo m
// Recursive function to
// return gcd of a and b
function __gcd($a, $b)
{
// Everything divides 0
if ($a == 0 || $b == 0)
return 0;
// base case
if ($a == $b)
return $a;
// a is greater
if ($a > $b)
return __gcd($a-$b, $b);
return __gcd($a, $b-$a);
}
// Function to find modular
// inverse of a under modulo m
// Assumption: m is prime
function modInverse($a, $m)
{
if (__gcd($a, $m) != 1)
echo "Inverse doesn't exist";
else
{
// If a and m are relatively
// prime, then modulo inverse
// is a^(m-2) mode m
echo "Modular multiplicative inverse is ",
power($a,$m - 2, $m);
}
}
// To compute x^y under modulo m
function power($x, $y, $m)
{
if ($y == 0)
return 1;
$p = power($x,$y / 2, $m) % $m;
$p = ($p * $p) % $m;
return ($y % 2 == 0) ? $p : ($x * $p) % $m;
}
// Driver Code
$a = 3; $m = 11;
modInverse($a, $m);
// This code is contributed by anuj__67.
?>
Javascript
<script>
// Javascript program to find modular inverse of a
// under modulo m using Fermat's little theorem.
// This program works only if m is prime.
function __gcd(a, b)
{
if(b == 0)
{
return a;
}
else
{
return __gcd(b, a % b);
}
}
// Function to find modular inverse of a under modulo m
// Assumption: m is prime
function modInverse(a, m)
{
if (__gcd(a, m) != 1)
document.write( "Inverse doesn't exist");
else {
// If a and m are relatively prime, then
// modulo inverse is a^(m-2) mode m
document.write( "Modular multiplicative inverse is "
+ power(a, m - 2, m));
}
}
// To compute x^y under modulo m
function power(x, y, m)
{
if (y == 0)
return 1;
var p = power(x, parseInt(y / 2), m) % m;
p = (p * p) % m;
return (y % 2 == 0) ? p : (x * p) % m;
}
// Driver Program
var a = 3, m = 11;
modInverse(a, m);
// This code is contributed by rutvik_56.
</script>
Producción :
Modular multiplicative inverse is 4
Algún artículo basado en el pequeño teorema de Fermat
- Calcule nCr % p | Conjunto 3 (usando el pequeño teorema de Fermat)
- Inverso multiplicativo modular
- Prueba de primalidad | Juego 2 (Método Fermat)
- Módulo 10^9+7 (1000000007)
Publicación traducida automáticamente
Artículo escrito por Nishant_Singh y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA