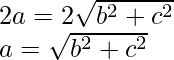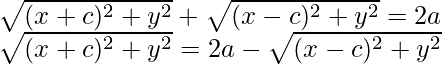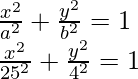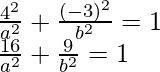Elipse – Barcelona Geeks

Las secciones cónicas son las figuras o curvas que se generan a partir de las secciones del cono. Se generan diferentes curvas cuando cortamos el cono con un plano en diferentes ángulos. Elipse es también parte de secciones cónicas. Otras secciones cónicas incluyen: círculos, parábolas, hipérbolas, etc. Nos encontramos con elipses en muchos lugares de nuestras vidas, por ejemplo: una pelota de rugby o un huevo tienen forma ovalada, que cuando se proyectan en 2D nos dan una elipse. El movimiento planetario es también otro ejemplo de la elipse. Los planetas giran alrededor del sol en forma de elipse. Para nosotros es fundamental estudiar la elipse para poder trabajar en estos problemas. Introduzcamos la elipse y veamos sus propiedades en detalle.

Introducción a la elipse

Una elipse es un conjunto de puntos en un plano, la suma de cuyas distancias a dos puntos fijos en el plano es constante. Los dos puntos fijos se llaman focos de la elipse. La siguiente figura muestra los dos puntos fijos y muestra cómo se puede trazar una elipse desde esos puntos.

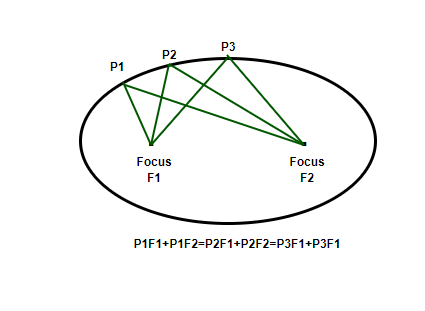
UN ₁ F ₁ + UN ₁ F ₂ = UN ₂ F ₁ + UN ₂ F ₂ = UN ₃ F ₁ + UN ₃ F ₂

Nota: La distancia constante que se menciona arriba siempre debe ser menor que la distancia entre los dos puntos focales.

La siguiente figura muestra un diagrama etiquetado de la elipse.

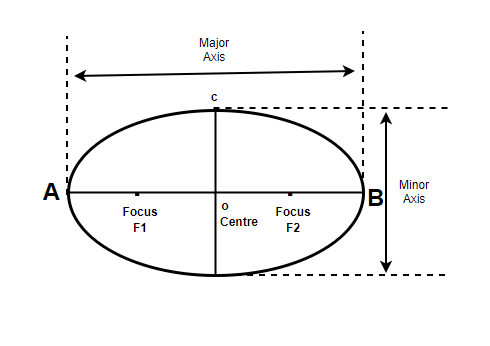
El segmento de línea que une y pasa por dos focos se llama eje mayor . El punto medio del segmento de recta entre dos focos se llama centro de la elipse. La recta perpendicular al eje mayor y que pasa por el centro de la elipse se llama eje menor . Los extremos del eje mayor que cortan la elipse se llaman vértices de la elipse.

Digamos que la longitud del eje mayor es 2a y mientras que la del eje menor es 2b. La distancia entre dos focos se define como 2c. El siguiente diagrama muestra los ejes y sus longitudes.

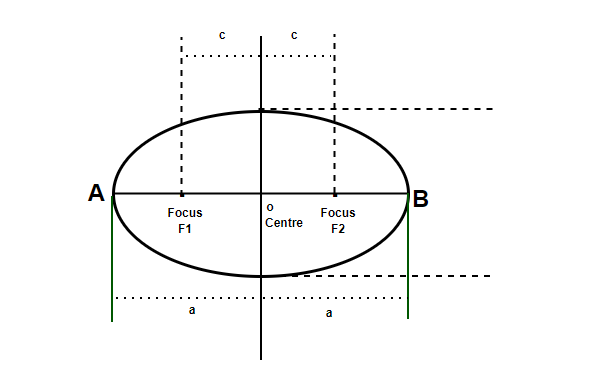
Otras secciones, introducen las propiedades y la ecuación de la elipse.

Relación entre los ejes mayor y menor

Hemos definido los ejes mayor y menor en las secciones anteriores. Ahora la pregunta que viene a la mente es si están relacionados entre sí de alguna manera. ¿Hay algún caso especial de la elipse? Primero, establezcamos la relación entre los ejes mayor y menor.

Considere el punto A. La distancia de A desde los dos centros es,

AF ₁ + AF ₂ = OF ₁ + OA + AF ₂

= c + a + a – c = 2a

Desde el punto B en el eje menor.

F ₁ segundo + F _{2 segundo} = $2\sqrt{b^2 + c^2}$

Sabemos por la definición de la elipse que,

AF ₁ + AF ₂ = F ₁ B + F ₂ B

$2a = 2\sqrt{b^2 + c^2}\\ a = \sqrt{b^2 + c^2}$

Excentricidad

La excentricidad de una elipse es la razón de las distancias desde el centro de la elipse a uno de los focos y a uno de los vértices de la elipse

$e = \frac{c}{a}$

Ecuación de Elipse

La siguiente figura representa una elipse estándar, con F ₁ y F ₂ como focos y O como el punto medio del segmento de línea F ₁ F ₂ . Supongamos que hay un punto en la elipse P(x, y). Sabemos,

FP ₁ + FP ₂ = 2a

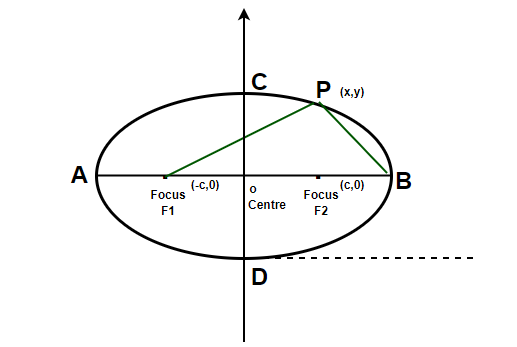
Usaremos la fórmula de la distancia para sustituir los valores de BF _1, BF ₂ .

$\sqrt{(x +c)^2 + y^2} + \sqrt{(x-c)^2 + y^2} = 2a \\ \sqrt{(x +c)^2 + y^2} = 2a - \sqrt{(x-c)^2 + y^2}$

Cuadrando ambos lados,

(x +c) ² + y ² = 4a ² + (xc) ² + y ² + 2y(xc)

x ² + c ² + 2xc + y ² = 4a ² + x ² + c ² + -2xc + y ² + 2xy – 2yc

Tras la simplificación,

$\\ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

Las siguientes figuras representan los otros casos posibles para la elipse.

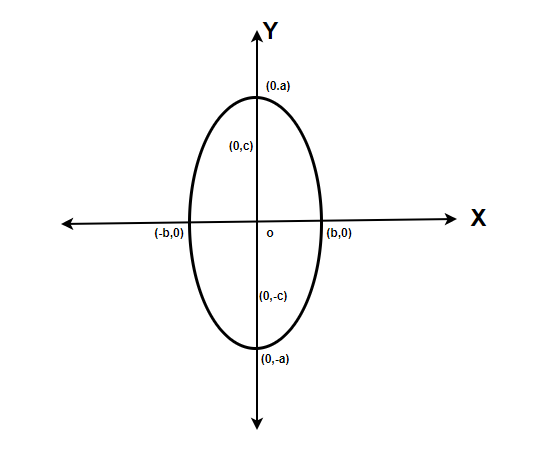
La ecuación para esta elipse será,

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

Lato Recto

Este es un segmento de recta que pasa por ambos focos y es perpendicular al eje mayor. Sus extremos se encuentran en su intersección con la elipse. Sea la longitud del AF ₂ l.

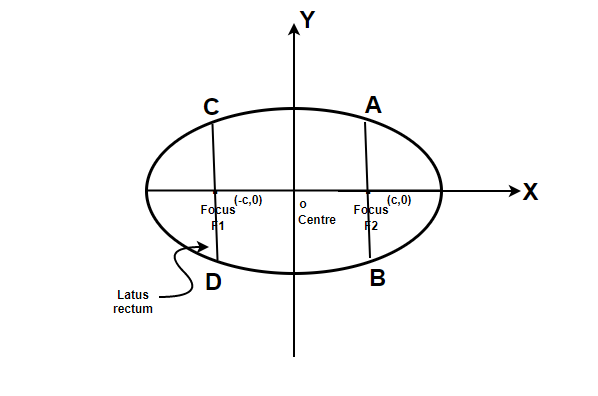
Ahora las coordenadas de A serán (c, l). Ahora sabemos que A se encuentra en la elipse, por lo que satisfará la ecuación de la elipse.

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \\ \frac{c^2}{a^2} + \frac{l^2}{b^2} = 1 \\ \text{We know, c = ae} \\ e^2 + \frac{l^2}{b^2} = 1 \\ l^2 = b^2 (1 - e^2) \\ l = b\sqrt{1 - e^2}\\$

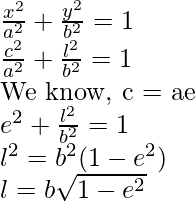
Problemas de muestra

Pregunta 1: Encuentra la ecuación de la elipse si los extremos del eje mayor se encuentran en (-10,0) y (10,0) y los extremos del eje menor se encuentran en (0,-5) y (0,5).

Solución:

Dado que el eje mayor es el eje x, la ecuación de la elipse debe ser,

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

2a = 20

⇒a = 10

2b = 10

⇒b = 5

$\frac{x^2}{10^2} + \frac{y^2}{5^2} = 1$

Pregunta 2: Encuentra la ecuación de una elipse con el origen como centro y el eje x como eje mayor. Dado que la distancia entre dos focos es de 10 cm, e = 0,4 y b = 4 cm

Solución:

La ecuación estándar de la elipse es,

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

Sabemos b = 4, e = 0,4 y c = 10.

$c = ae \\ 10 = a(0.4) \\ 25 = a$

Entonces, ahora tenemos a = 25 y b = 4

Entonces, la ecuación de la elipse es,

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \\ \frac{x^2}{25^2} + \frac{y^2}{4^2} = 1$

Pregunta 3: Encuentra la ecuación de una elipse cuyo eje mayor es de 40 cm y los focos se encuentran en (5,0) y (-5,0).

Solución:

$\frac{x^2}{a^2} + \frac{x^2}{b^2} = 1$

un = $\frac{40}{2} = 20$

Sabemos c = 10

do ² = un ² – ^{segundo 2}

10 ² = 20 ² – ^{segundo 2}

b ² = 20 ² – 10 ²

b2 ⁼ 300

Por lo tanto, la ecuación se convierte en,

$\frac{x^2}{400} + \frac{x^2}{300} = 1$

Pregunta 4: Encuentra la ecuación de una elipse cuyo eje mayor es de 40 cm y los focos se encuentran en (0,5) y (0,-5).

Solución:

Dado que los focos se encuentran en el eje y. El eje mayor está en el eje y. Por lo tanto, la elipse es de la forma,

$\frac{x^2}{b^2} + \frac{x^2}{a^2} = 1$

un = $\frac{40}{2} = 20$

Sabemos c = 10

do ² = un ² – ^{segundo 2}

10 ² = 20 ² – ^{segundo 2}

b ² = 20 ² – 10 ²

b2 ⁼ 300

Por lo tanto, la ecuación se convierte en,

$\frac{x^2}{300} + \frac{x^2}{400} = 1$

Pregunta 5: Encuentra la ecuación de la elipse si el eje mayor es el eje x y el eje menor es el eje y y (4,3) y (-1,4) se encuentran en la elipse.

Solución:

La ecuación estándar de la elipse es,

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

Estos puntos deben satisfacer la ecuación. (4,3) y (-1, 4).

$\frac{4^2}{a^2} + \frac{(-3)^2}{b^2} = 1 \\ \frac{16}{a^2} + \frac{9}{b^2} = 1 \\$

$\frac{(-1)^2}{a^2} + \frac{4^2}{b^2} = 1 \\ \frac{1}{a^2} + \frac{16}{b^2} = 1 \\$

Digamos, $x = \frac{1}{a} \text{ and } y = \frac{1}{b}$

16x + 9b = 1

x + 16b = 1

Resolviendo las ecuaciones,

Encontramos eso $a = \frac{247}{7} \text{ and } b = \frac{247}{15}$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Introducción a la elipse

Relación entre los ejes mayor y menor

Ecuación de Elipse

Lato Recto

Problemas de muestra

Deja una respuesta Cancelar la respuesta