La trigonometría es la rama de las matemáticas que se ocupa de los triángulos y los ángulos asociados a ella. Si la palabra se divide en 2 partes, a saber, trigon y geometría, se puede entender fácilmente que esta rama de las matemáticas se ocupa de la geometría de los triángulos. Usando la trigonometría, las propiedades de los triángulos y sus aplicaciones pueden entenderse fácilmente. Usando trigonometría, uno puede encontrar los ángulos y los lados faltantes de cualquier triángulo con el uso de razones trigonométricas.
razones trigonométricas
Hay seis funciones o razones trigonométricas de un ángulo que están presentes en la trigonometría. Sus nombres y abreviaturas son seno (sin), coseno (cos), tangente (tan), cotangente (cot), secante (sec) y cosecante (csc). Una cosa importante a tener en cuenta aquí es que las fórmulas trigonométricas solo funcionan en el triángulo rectángulo. Veamos la imagen de abajo.
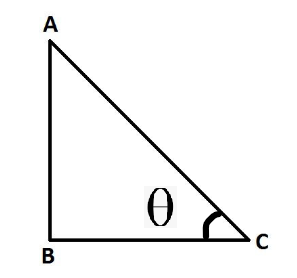
En este triángulo rectángulo, el lado AC se conoce como hipotenusa. El lado BC se conoce como la base del triángulo. el lado AB se conoce como la altura del triángulo. Desde el triángulo anterior, podemos enumerar fórmulas como arriba,
- sen∅ = AB/AC
- cos∅ = BC/AC
- tan∅ = AB/BC
- cuna∅ = BC/AB
- cosec∅ = AC/AB
- seg∅ = AC/BC
Fórmulas básicas de razones trigonométricas
- Tan ∅ = sen ∅/cos ∅
- sen ∅ = 1/coseg ∅
- cos ∅ = 1/seg ∅
- Tan ∅ = 1/cuna ∅
En un triángulo XYZ con ángulo recto en Y, encuentre la longitud del lado de YZ, si XY = 5 cm y ∠C = 30°
Solución:
Entendamos este problema con la ayuda de la siguiente figura,
Lo que se necesita encontrar es la base del triángulo YZ. El dato que se da es el ángulo Z es 30 y XY = 5
tan ∅ = XY/YZ
tan30 = 5/YZ
YZ = 5√3 (ya que tan30 = 1/√3)
Problemas similares
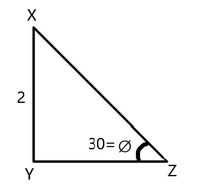
Pregunta 1: En un triángulo XYZ, que es rectángulo en Y, encuentra la longitud del lado de XZ, si XY = 2 cm y ∠Z = 30°
Solución:
Dado, XY = 2 cm y ∠Z = 30°
Para encontrar – XZ
sen∅ = XY/XZ
sen30 = 2/XZ
XZ = 2/sen30
= 4 (ya que sen30° es 1/2)
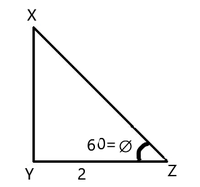
Pregunta 2: En un triángulo XYZ, que es rectángulo en Y, encuentra la longitud del lado de XY, si YZ = 2 cm y ∠Z = 60°
Solución:
Dado, YZ = 2 cm y ∠Z = 60°
Para encontrar – XY?
tan∅ = XY/YZ
tan60 = XY/2
XY = 2√3 (ya que tan60° es √3)
Publicación traducida automáticamente
Artículo escrito por pradiptamukherjee y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
