Encontrar el camino desde un vértice hasta el resto usando BFS

Dada una representación de lista de adyacencia de un gráfico dirigido, la tarea es encontrar la ruta desde el origen hasta todos los demás Nodes del gráfico usando BFS .
Ejemplos: 
 

Input:

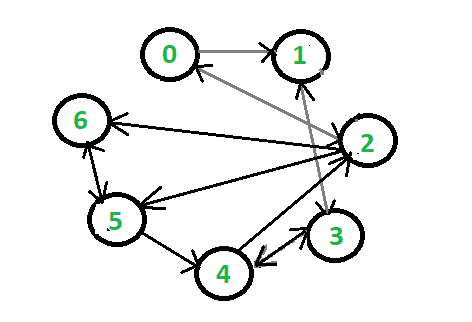
Output:
0 <- 2
1 <- 0 <- 2
2
3 <- 1 <- 0 <- 2
4 <- 5 <- 2
5 <- 2
6 <- 2

Enfoque: En las imágenes que se muestran a continuación: 
 

• La array que[] almacena los vértices alcanzados y pondremos en cola un vértice solo si no ha sido visitado y lo quitaremos de la cola una vez que se hayan considerado todos sus Nodes secundarios.
• Para distinguir si el Node ha sido visitado o no, pondremos 1 en la array visited[] en el índice respectivo para indicar que ha sido visitado y si en el índice 0 está presente, significará que no ha sido visitado.
• La array principal es para almacenar el Node principal de cada vértice. por ej. En el caso de 0 conectado a 2, 2 será el Node principal de 0 y pondremos 2 en el índice 0 en la array principal.

A continuación se muestra la implementación del enfoque anterior:
 

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to print the path from
// source (s) to destination (d)
void print(vector<int> parent, int s, int d)
{
   
  // The while loop will stop only when the
  // destination and the source node become equal
  while (s != d)
  {
 
      // Print the destination and store the parent
      // of the node in the destination since parent
      // stores the node through which
      // the current node has been reached
      cout << d << " <- ";
      d = parent[d];
  }
  cout << d << endl;
}
 
// Finding Path using BFS ALgorithm
void bfs(vector<vector<int> > adjList, int source, int n)
{
    vector<int> parent(n, 0);
    vector<int> que(n, 0);
 
    int front = -1, rear = -1;
    vector<int> visited(n, 0);
   
    //Arrays.fill(visited, 0);
    visited = 1;
    parent = source;
 
    // To add any non visited node we will increment the rear
    // and add that vertex to the end of the array (enqueuing)
    que[++rear] = source;
    int k;
 
    // The loop will continue till the rear and front are equal
    while (front != rear)
    {
 
        // Here Dequeuing is nothing but to increment the front int
        k = que[++front];
       
        //L<Integer> list = adjList.get(k);
        for (int j:adjList[k])
        {
            if (visited[j] == 0)
            {
                que[++rear] = j;
                visited[j] = 1;
                parent[j] = k;
            }
        }
    }
 
    // Print the path from source to every other node
    for (k = 0; k < n; k++)
        print(parent, source, k);
}
 
// Driver code
int main()
{
 
    // Adjacency list representation of the graph
    vector<vector<int> > adjList;
 
    // Vertices 1 and 2 have an incoming edge
    // from vertex 0
    adjList.push_back({1, 2});
 
    // Vertex 3 has an incoming edge
    // from vertex 1
    adjList.push_back({3});
 
    // Vertices 0, 5 and 6 have an incoming
    // edge from vertex 2
    adjList.push_back({0, 5, 6});
 
    // Vertices 1 and 4 have an incoming edge
    // from vertex 3
    adjList.push_back({1, 4});
 
    // Vertices 2 and 3 have an incoming edge
    // from vertex 4
    adjList.push_back({2, 3});
 
    // Vertices 4 and 6 have an incoming edge
    // from vertex 5
    adjList.push_back({4, 6});
 
    // Vertex 5 has an incoming edge
    // from vertex 6
    adjList.push_back({5});
    int n = adjList.size();
    int source = 2;
    bfs(adjList, source, n);
}
 
// This code is contributed by mohit kumar 29.

// Java implementation of the approach
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
 
class GFG
{
 
    // Function to print the path from
    // source (s) to destination (d)
    static void print(int parent[], int s, int d)
    {
        // The while loop will stop only when the
        // destination and the source node become equal
        while (s != d) {
 
            // Print the destination and store the parent
            // of the node in the destination since parent
            // stores the node through which
            // the current node has been reached
            System.out.print(d + " <- ");
            d = parent[d];
        }
 
        System.out.println(d);
    }
 
    // Finding Path using BFS ALgorithm
    static void bfs(List<List<Integer> > adjList, int source, int n)
    {
        int parent[] = new int[n];
        int que[] = new int[n];
        Arrays.fill(parent, 0);
        Arrays.fill(que, 0);
 
        int front = -1, rear = -1;
        int visited[] = new int[n];
        Arrays.fill(visited, 0);
        visited = 1;
        parent = source;
 
        // To add any non visited node we will increment the rear
        // and add that vertex to the end of the array (enqueuing)
        que[++rear] = source;
 
        int k;
 
        // The loop will continue till the rear and front are equal
        while (front != rear) {
 
            // Here Dequeuing is nothing but to increment the front int
            k = que[++front];
            List<Integer> list = adjList.get(k);
            for (int i = 0; i < list.size(); i++) {
                int j = list.get(i);
                if (visited[j] == 0) {
                    que[++rear] = j;
                    visited[j] = 1;
                    parent[j] = k;
                }
            }
        }
 
        // Print the path from source to every other node
        for (k = 0; k < n; k++)
            print(parent, source, k);
    }
 
    // Driver code
    public static void main(String args[])
    {
 
        // Adjacency list representation of the graph
        List<List<Integer> > adjList = new ArrayList<>();
 
        // Vertices 1 and 2 have an incoming edge
        // from vertex 0
        List<Integer> tmp = new ArrayList<Integer>(Arrays.asList(1, 2));
        adjList.add(tmp);
 
        // Vertex 3 has an incoming edge from vertex 1
        tmp = new ArrayList<Integer>(Arrays.asList(3));
        adjList.add(tmp);
 
        // Vertices 0, 5 and 6 have an incoming
        // edge from vertex 2
        tmp = new ArrayList<Integer>(Arrays.asList(0, 5, 6));
        adjList.add(tmp);
 
        // Vertices 1 and 4 have an incoming edge
        // from vertex 3
        tmp = new ArrayList<Integer>(Arrays.asList(1, 4));
        adjList.add(tmp);
 
        // Vertices 2 and 3 have an incoming edge
        // from vertex 4
        tmp = new ArrayList<Integer>(Arrays.asList(2, 3));
        adjList.add(tmp);
 
        // Vertices 4 and 6 have an incoming edge
        // from vertex 5
        tmp = new ArrayList<Integer>(Arrays.asList(4, 6));
        adjList.add(tmp);
 
        // Vertex 5 has an incoming edge from vertex 6
        tmp = new ArrayList<Integer>(Arrays.asList(5));
        adjList.add(tmp);
 
        int n = adjList.size();
 
        int source = 2;
        bfs(adjList, source, n);
    }
}

# Python3 implementation of the approach
 
# Function to print the path from
# src (s) to destination (d)
def printfunc(parent, s, d):
     
    # The while loop will stop only when
    # the destination and the src node
    # become equal
    while s != d:
 
        # Print the destination and store
        # the parent of the node in the
        # destination since parent stores
        # the node through which the current
        # node has been reached
        print(str(d) + " <-", end = " ")
        d = parent[d]
         
    print(d)
 
# Finding Path using BFS ALgorithm
def bfs(adjList, src, n):
     
    parent = [0] * (n)
    que = [0] * (n)
     
    front, rear = -1, -1
    visited = [0] * (n)
    visited[src] = 1
    parent[src] = src
 
    # To add any non visited node we will
    # increment the rear and add that vertex
    # to the end of the array (enqueuing)
    rear += 1
    que[rear] = src
 
    # The loop will continue till the rear
    # and front are equal
    while front != rear:
 
        # Here Dequeuing is nothing but to
        # increment the front int
        front += 1
        k = que[front]
        List = adjList[k]
        for i in range(0, len(List)):
            j = List[i]
             
            if visited[j] == 0:
                rear += 1
                que[rear] = j
                visited[j] = 1
                parent[j] = k
                 
    # Print the path from src to every
    # other node
    for k in range(0, n):
        printfunc(parent, src, k)
     
# Driver code
if __name__ == "__main__":
 
    # Adjacency list representation
    # of the graph
    adjList = []
 
    # Vertices 1 and 2 have an incoming edge
    # from vertex 0
    adjList.append([1, 2])
 
    # Vertex 3 has an incoming edge
    # from vertex 1
    adjList.append([3])
 
    # Vertices 0, 5 and 6 have an incoming
    # edge from vertex 2
    adjList.append([0, 5, 6])
 
    # Vertices 1 and 4 have an incoming edge
    # from vertex 3
    adjList.append([1, 4])
 
    # Vertices 2 and 3 have an incoming edge
    # from vertex 4
    adjList.append([2, 3])
 
    # Vertices 4 and 6 have an incoming edge
    # from vertex 5
    adjList.append([4, 6])
 
    # Vertex 5 has an incoming edge
    # from vertex 6
    adjList.append([5])
 
    n = len(adjList)
 
    src = 2
    bfs(adjList, src, n)
     
# This code is contributed by Rituraj Jain

<script>
 
// JavaScript implementation of the approach
     
    // Function to print the path from
    // source (s) to destination (d)
    function print(parent,s,d)
    {
        // The while loop will stop only when the
        // destination and the source node become equal
        while (s != d) {
  
            // Print the destination and store the parent
            // of the node in the destination since parent
            // stores the node through which
            // the current node has been reached
            document.write(d + " <- ");
            d = parent[d];
        }
  
        document.write(d+"<br>");
    }
     
    // Finding Path using BFS ALgorithm
    function bfs( adjList,source,n)
    {
        let parent = new Array(n);
        let que = new Array(n);
        for(let i=0;i<n;i++)
        {
            parent[i]=0;
            que[i]=0;
        }
  
        let front = -1, rear = -1;
        let visited = new Array(n);
        for(let i=0;i<n;i++)
        {
            visited[i]=0;
        }
        visited = 1;
        parent = source;
  
        // To add any non visited node we will increment the rear
        // and add that vertex to the end of the array (enqueuing)
        que[++rear] = source;
  
        let k;
  
        // The loop will continue till the rear
        // and front are equal
        while (front != rear) {
  
            // Here Dequeuing is nothing but
            // to increment the front int
            k = que[++front];
            let list = adjList[k];
            for (let i = 0; i < list.length; i++) {
                let j = list[i];
                if (visited[j] == 0) {
                    que[++rear] = j;
                    visited[j] = 1;
                    parent[j] = k;
                }
            }
        }
  
        // Print the path from source to every other node
        for (k = 0; k < n; k++)
            print(parent, source, k);
    }
     
     // Driver code
     
    // Adjacency list representation of the graph
        let adjList = [];
  
        // Vertices 1 and 2 have an incoming edge
        // from vertex 0
        adjList.push([1, 2])
         
  
        // Vertex 3 has an incoming edge from vertex 1
        adjList.push([3])
  
        // Vertices 0, 5 and 6 have an incoming
        // edge from vertex 2
        adjList.push([0, 5, 6])
  
        // Vertices 1 and 4 have an incoming edge
        // from vertex 3
        adjList.push([1, 4])
  
        // Vertices 2 and 3 have an incoming edge
        // from vertex 4
        adjList.push([2, 3])
  
        // Vertices 4 and 6 have an incoming edge
        // from vertex 5
        adjList.push([4, 6])
  
        // Vertex 5 has an incoming edge from vertex 6
        adjList.push([5])
  
        let n = adjList.length;
  
        let source = 2;
        bfs(adjList, source, n);
 
 
// This code is contributed by unknown2108
 
</script>

0 <- 2
1 <- 0 <- 2
2
3 <- 1 <- 0 <- 2
4 <- 5 <- 2
5 <- 2
6 <- 2

Complejidad temporal : O(V + E) donde V y E son los números de vértices y aristas en el gráfico respectivamente.
Espacio Auxiliar : O(V + E).