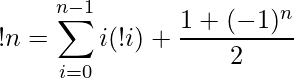Dado un número entero N, la tarea es encontrar el subfactorial del número representado como !N. El subfactorial de un número se define usando la siguiente relación de recurrencia de un número N :
!N = (N-1) [ !(N-2) + !(N-1) ]
donde !1 = 0 y !0 = 1
Algunos de los subfactoriales son:
| norte | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ! norte | 1 | 0 | 1 | 2 | 9 | 44 | 265 | 1, 854 | 14, 833 | 133, 496 | 1, 334, 961 | 14, 684, 570 | 176, 214, 841 | 2, 290, 792, 932 |
Ejemplos:
Entrada: N = 4
Salida: 9
Explicación:
!4 = !(4-1)*4 + (-1) 4 = !3*4 + 1
!3 = !(3 – 1)*3 + (-1) 3 = !2*3 – 1
!2 = !(2 – 1)*2 + (-1) 2 = !1*2 + 1
!1 = !(1 – 1)*1 + (-1) 1 = !0*1 – 1
Dado que !0 = 1, por lo tanto, !1 = 0, !2 = 1, !3 = 2 y !4 = 9.Entrada: N = 0
Salida: 1
Enfoque: El subfactorial del número N también se puede calcular como:
Expandiendo esto da
=> !N = ( N! )*( 1 – 1/(1!) + (1/2!) – (1/3!) …….. (1/N!)*(-1) N )
Por lo tanto, la serie anterior se puede usar para encontrar el subfactorial del número N. Siga los pasos a continuación para ver cómo:
- Inicialice las variables, digamos res = 0 , fact = 1 y count = 0 .
- Itere sobre el rango de 1 a N usando i y haga lo siguiente:
- Actualizar hecho como hecho*i.
- Si el recuento es par , actualice res como res = res – (1 / fact) .
- Si el recuento es impar , actualice res como res = res + (1 / fact) .
- Aumente el valor de la cuenta en 1.
- Finalmente, devuelve fact*(1 + res) .
A continuación se muestra la implementación del enfoque anterior:
C++
/// C++ program for the above approach
#include <iostream>
using namespace std;
// Function to find the subfactorial
// of the number
double subfactorial(int N)
{
// Initialize variables
double res = 0, fact = 1;
int count = 0;
// Iterating over range N
for (int i = 1; i <= N; i++) {
// Fact variable store
// factorial of the i
fact = fact * i;
// If count is even
if (count % 2 == 0)
res = res - (1 / fact);
else
res = res + (1 / fact);
// Increase the value of
// count by 1
count++;
}
return fact * (1 + res);
}
// Driver Code
int main()
{
int N = 4;
cout << subfactorial(N);
return 0;
}
Java
/// Java program for the above approach
import java.util.*;
class GFG {
// Function to find the subfactorial
// of the number
static double subfactorial(int N)
{
// Initialize variables
double res = 0, fact = 1;
int count = 0;
// Iterating over range N
for (int i = 1; i <= N; i++) {
// Fact variable store
// factorial of the i
fact = fact * i;
// If count is even
if (count % 2 == 0)
res = res - (1 / fact);
else
res = res + (1 / fact);
// Increase the value of
// count by 1
count++;
}
return fact * (1 + res);
}
// Driver Code
public static void main(String[] args)
{
int N = 4;
System.out.println((int)(subfactorial(N)));
}
}
// This code is contributed by ukasp.
Python3
# python program for the above approach # Function to find the subfactorial # of the number def subfactorial(N): # Initialize variables res = 0 fact = 1 count = 0 # Iterating over range N for i in range(1, N+1): # Fact variable store # factorial of the i fact = fact * i # If count is even if (count % 2 == 0): res = res - (1 / fact) else: res = res + (1 / fact) # Increase the value of # count by 1 count += 1 return fact * (1 + res) # Driver Code if __name__ == "__main__": N = 4 print(subfactorial(N)) # This code is contributed by rakeshsahni
C#
/// C# program for the above approach
using System;
using System.Collections.Generic;
class GFG{
// Function to find the subfactorial
// of the number
static double subfactorial(int N)
{
// Initialize variables
double res = 0, fact = 1;
int count = 0;
// Iterating over range N
for (int i = 1; i <= N; i++) {
// Fact variable store
// factorial of the i
fact = fact * i;
// If count is even
if (count % 2 == 0)
res = res - (1 / fact);
else
res = res + (1 / fact);
// Increase the value of
// count by 1
count++;
}
return fact * (1 + res);
}
// Driver Code
public static void Main()
{
int N = 4;
Console.Write(subfactorial(N));
}
}
// This code is contributed by ipg2016107.
Javascript
<script>
// JavaScript Program to implement
// the above approach
// Function to find the subfactorial
// of the number
function subfactorial(N) {
// Initialize variables
let res = 0, fact = 1;
let count = 0;
// Iterating over range N
for (let i = 1; i <= N; i++) {
// Fact variable store
// factorial of the i
fact = fact * i;
// If count is even
if (count % 2 == 0)
res = res - 1 / fact;
else
res = res + 1 / fact;
// Increase the value of
// count by 1
count++;
}
return fact * (1 + res);
}
// Driver Code
let N = 4;
document.write(subfactorial(N));
// This code is contributed by Potta Lokesh
</script>
9
Complejidad temporal: O(N)
Espacio auxiliar: O(1)