Encontrar el vértice, el foco y la directriz de una parábola

Problema: encuentre el vértice, el foco y la directriz de una parábola cuando se dan los coeficientes de su ecuación.
Un conjunto de puntos en una superficie plana que forma una curva tal que cualquier punto en esa curva es equidistante del foco es una parábola.  
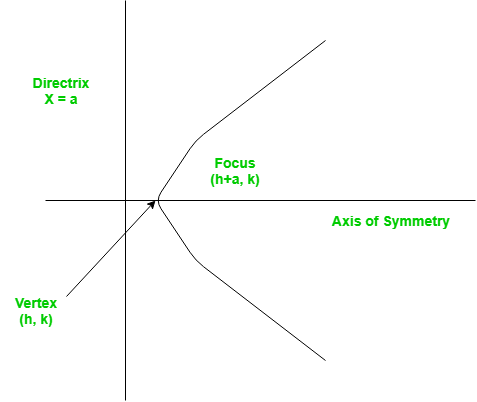
El vértice de una parábola es la coordenada desde la que toma el giro más cerrado, mientras que a es la línea recta utilizada para generar la curva. 
 

La forma estándar de una ecuación de parábola es  . Dados los valores de a, b y c; nuestra tarea es encontrar las coordenadas de vértice, foco y la ecuación de la directriz. 
Ejemplo – 
 

Input : 5 3 2
Output : Vertex:(-0.3, 1.55)
         Focus: (-0.3, 1.6)
         Directrix: y=-198
Consult the formula below for explanation.

Este problema es un ejemplo simple de implementaciones de fórmulas. A continuación se presenta el conjunto de fórmulas necesarias que nos ayudarán a abordar el problema. 
 

For a parabola in the form Vertex: Focus: Directrix: 

#include <iostream>
using namespace std;
 
// Function to calculate Vertex, Focus and Directrix
void parabola(float a, float b, float c)
{
    cout << "Vertex: (" << (-b / (2 * a)) << ", "
         << (((4 * a * c) - (b * b)) / (4 * a))
         << ")" << endl;
    cout << "Focus: (" << (-b / (2 * a)) << ", "
         << (((4 * a * c) - (b * b) + 1) / (4 * a))
         << ")" << endl;
    cout << "Directrix: y="
         << c - ((b * b) + 1) * 4 * a << endl;
}
 
// Driver Function
int main()
{
    float a = 5, b = 3, c = 2;
    parabola(a, b, c);
    return 0;
}

// Java program to find the vertex,
// focus and directrix of a parabola
 
class GFG {
     
    // Function to calculate Vertex,
    // Focus and Directrix
    static void parabola(float a,
                         float b, float c)
    {
         
        System.out.println("Vertex: (" +
                          (-b / (2 * a)) + ", " +
                          (((4 * a * c) - (b * b)) /
                          (4 * a)) + ")");
                     
        System.out.println("Focus: (" +
                          (-b / (2 * a)) + ", "    +
                          (((4 * a * c) - (b * b) + 1) /
                          (4 * a)) + ")");
             
        System.out.println("Directrix:" + " y=" +
                          (int)(c - ((b * b) + 1) *
                          4 * a));
    }
 
    // Driver Function
    public static void main(String[] args)
    {
        float a = 5, b = 3, c = 2;
         
        // Function calling
        parabola(a, b, c);
    }
}
 
// This code is contributed by
// Smitha Dinesh Semwal

# Function to calculate Vertex,
# Focus and Directrix
def parabola(a, b, c):
 
    print("Vertex: (" , (-b / (2 * a)),
        ", ", (((4 * a * c) - (b * b))
            / (4 * a)), ")", sep = "")
               
    print("Focus: (" , (-b / (2 * a)),
    ", ", (((4 * a * c) - (b * b) + 1)
            / (4 * a)), ")", sep = "")
                
    print("Directrix: y=", c - ((b * b)
                + 1) * 4 * a, sep = "")
 
# Driver Function
a = 5
b = 3
c = 2
parabola(a, b, c)
 
# This code is contributed by Smitha.

// C# program to find the vertex,
// focus and directrix of a parabola
using System;
 
class GFG {
     
    // Function to calculate Vertex,
    // Focus and Directrix
    static void parabola(float a,
                         float b, float c)
    {
        Console.WriteLine("Vertex: (" +
                         (-b / (2 * a)) + ", " +
                         (((4 * a * c) - (b * b)) /
                         (4 * a)) + ")");
                     
        Console.WriteLine("Focus: (" +
                         (-b / (2 * a)) + ", " +
                         (((4 * a * c) - (b * b) + 1) /
                         (4 * a)) + ")");
                 
        Console.Write("Directrix:" + " y=" +
                     (int)(c - ((b * b) + 1) * 4 * a));
    }
 
    // Driver Function
    public static void Main()
    {
        float a = 5, b = 3, c = 2;
         
        // Function calling
        parabola(a, b, c);
    }
}
 
// This code is contributed by nitin mittal

<?php
// PHP program to Find the vertex,
// focus and directrix of a parabola
 
// Function to calculate Vertex,
// Focus and Directrix
function parabola($a, $b, $c)
{
     
    echo "Vertex: (" , (-$b / (2 * $a)) , ", ",
        (((4 * $a * $c) - ($b * $b)) / (4 * $a)),
                                      ")", "\n" ;
    echo "Focus: (" , (-$b / (2 * $a)) , ", ",
        (((4 * $a * $c) - ($b * $b) + 1) / (4 * $a))
                                        , ")"," \n" ;
    echo "Directrix: y=",
        $c - (($b * $b) + 1) * 4 * $a ;
}
 
    // Driver Code
    $a = 5; $b = 3; $c = 2;
    parabola($a, $b, $c);
     
// This code is contributed by vt_m.
?>

<script>
 
// JavaScript program to find the vertex,
// focus and directrix of a parabola
 
    // Function to calculate Vertex,
    // Focus and Directrix
    function parabola(a, b, c)
    {
           
        document.write("Vertex: (" +
                          (-b / (2 * a)) + ", " +
                          (((4 * a * c) - (b * b)) /
                          (4 * a)) + ")" + "<br/>");
                       
       document.write("Focus: (" +
                          (-b / (2 * a)) + ", "    +
                          (((4 * a * c) - (b * b) + 1) /
                          (4 * a)) + ")" + "<br/>");
               
        document.write("Directrix:" + " y=" +
                          (c - ((b * b) + 1) *
                          4 * a) + "<br/>");
    }
 
// Driver code
 
        let a = 5, b = 3, c = 2;
           
        // Function calling
        parabola(a, b, c);
             
            // This code is contributed by code_hunt.
</script>

Producción – 
 

Vertex:(-0.3, 1.55)
Focus: (-0.3, 1.6)
Directrix: y=-198

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)