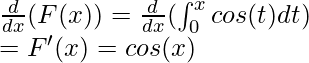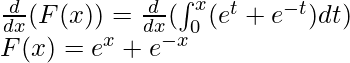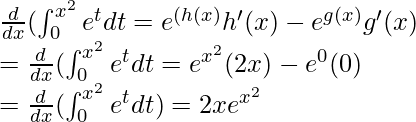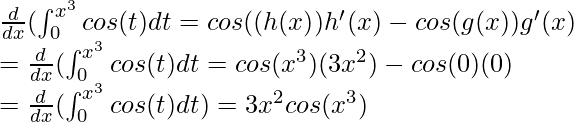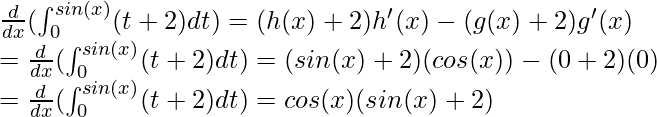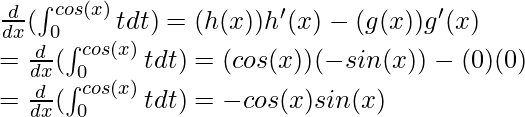Hallar derivadas con el teorema fundamental del cálculo

Las integrales son el proceso inverso de la diferenciación. También se denominan antiderivadas y se utilizan para encontrar las áreas y los volúmenes de formas arbitrarias para las que no disponemos de fórmulas. Las integrales indefinidas simplemente calculan la antiderivada de la función, mientras que las integrales definidas tienen límites y generalmente denotan el área bajo la curva. El teorema fundamental del cálculo relaciona las reglas integrales con las derivadas y las reglas de la string. Está acostumbrado a resolver problemas difíciles de integración. Veamos este teorema.

Aplicando el Teorema Fundamental del Cálculo

Considere una función f(x) como una función que es continua y derivable en el intervalo dado [a, b]. La integral definida entre estos límites se denota por $\int^{b}_{a}f(x)dx$ . Esta se define como el área encerrada por la función f(x) y el eje x entre los límites x = ay x = b. Esta integral definida se puede convertir en una función variando el límite superior del límite. Esta función se puede reescribir como,

deja $F(x) = \int^{x}_{a}f(t)dt$ _ Ahora, geométricamente, esta función nos da el área bajo la misma curva pero desde x = a hasta x, donde x se encuentra entre los límites de los límites. La siguiente figura muestra esta función:

Ahora en x = a, 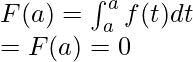$F(a) = \int^{a}_{a}f(t)dt \\ = F(a) = 0$

El teorema fundamental nos permite calcular las derivadas de la función dada.

Teorema Fundamental del Cálculo – Parte I

Para una función f que es continua y derivable en el intervalo [a, b], supongamos $F(x) = \int^{x}_{a}f(t)dt$ . Entonces, F es una función diferenciable en (a, b), y

F'(x) = f(x)

Este teorema parece trivial pero tiene implicaciones de gran alcance. Existe una función f(x) = x ² + sin(x),

Dado, F(x) = $\int^{x}_{-5}t^2 + sin(t)dt$

De acuerdo con el teorema fundamental mencionado anteriormente,

$\frac{d}{dx}F(x) = \frac{d}{dx}\int^{x}_{-5}(t^2 + sin(t))dt \\ F'(x) = x^2 + sin(x)$

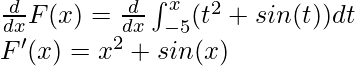
Este teorema se puede utilizar para derivar un resultado popular,

Supongamos que hay una integral definida $\int^{b}_{a}f(t)dt$ . Además, digamos F(x) = $\int^{x}_{c}f(t)dt$ .

$\int^{b}_{a}f(t)dt \\ = \int^{c}_{a}f(t)dt + \int^{b}_{c}f(t)dt \\ = -\int^{a}_{c}f(t)dx + \int^{b}_{c}f(t)dt \\ = -F(a) + F(b) \\ = F(b) - F(a)$

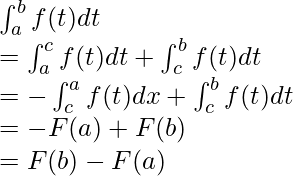
Esta es la segunda parte del Teorema Fundamental del Cálculo.

Teorema Fundamental del Cálculo – Parte II

Para una función f que es continua y derivable en el intervalo [a, b], sea F cualquier antiderivada de la función dada. Después,

$\int^{b}_{a}f(x)dx = F(b)- F(a)$

Aplicando el teorema fundamental con la regla de la string

Los problemas difíciles de integrales definidas se pueden resolver combinando la regla de la string y el teorema fundamental del cálculo. Por ejemplo,

$\frac{d}{dx}(\int^{x^2}_{1}cos(t)dt)$

Para resolver tales problemas, necesitamos una versión más generalizada del teorema fundamental.

Para una función f que es continua y otras dos funciones g y h que son diferenciables,

$\frac{d}{dx}\int^{h(x)}_{g(x)}f(s)ds = \frac{d}{dx}[F(h(x)) - F(g(x))] \\ = F'(h(x))h'(x) - F'(g(x))g'(x) \\ = f((h(x))h'(x) - f(g(x))g'(x)$

Veamos algunos problemas relacionados con estos conceptos.

Problemas de muestra

Pregunta 1: Dada la siguiente función F(x), calcula su derivada.

F(x) = $\int_{0}^{x}cos(t)dt$

Solución:

Dado: F(x) = $\int_{0}^{x}cos(t)dt$

$\frac{d}{dx}(F(x)) = \frac{d}{dx}(\int_{0}^{x}cos(t)dt)$

Esto se puede resolver usando el teorema fundamental de la parte de cálculo: I

$\frac{d}{dx}(F(x)) = \frac{d}{dx}(\int_{0}^{x}cos(t)dt) \\ = F'(x) = cos(x)$

Pregunta 2: Dada la siguiente función F(x), calcula su derivada.

F(x) = $\int_{0}^{x}(e^t + e^{-t})dt$

Solución:

Dado: F(x) = $\int_{0}^{x}(e^x + e^{-x})dt$

$\frac{d}{dx}(F(x)) = \frac{d}{dx}(\int_{0}^{x}(e^t + e^{-t})dt)$

Esto se puede resolver usando el teorema fundamental de la parte de cálculo: I

$\frac{d}{dx}(F(x)) = \frac{d}{dx}(\int_{0}^{x}(e^t + e^{-t})dt) \\ F(x) = e^x + e^{-x}$

Pregunta 3: Dada la siguiente función F(x), calcula su derivada.

F(x) = $\int_{0}^{x^2}e^tdt$

Solución:

Dado: F(x) = $\int_{0}^{x^2}e^tdt$

$\frac{d}{dx}(F(x)) = \frac{d}{dx}(\int_{0}^{x^2}e^tdt)$

Esto se puede resolver usando la forma generalizada del teorema fundamental del cálculo parte – I. Establece que,

$\frac{d}{dx}\int^{h(x)}_{g(x)}f(s)ds = \frac{d}{dx}[F(h(x)) - F(g(x))] \\ = F'(h(x))h'(x) - F'(g(x))g'(x) \\ = f((h(x))h'(x) - f(g(x))g'(x)$

Aquí, f(t) = e ^t , h(x) = x ² y g(x) = 0

$\frac{d}{dx}(\int^{x^2}_0e^tdt= e^{(h(x)}h'(x) - e^{g(x)}g'(x) \\ = \frac{d}{dx}(\int^{x^2}_0e^tdt = e^{x^2}(2x) - e^{0}(0) \\ = \frac{d}{dx}(\int^{x^2}_0e^tdt) = 2xe^{x^2}$

Pregunta 4: Dada la siguiente función F(x), calcula su derivada.

F(x) = $\int_{0}^{x^3}cos(t)dt$

Solución:

Dado: F(x) = $\int_{0}^{x^3}cos(t)dt$

$\frac{d}{dx}(F(x)) = \frac{d}{dx}(\int_{0}^{x^3}cos(t)dt)$

Esto se puede resolver usando la forma generalizada del teorema fundamental del cálculo parte – I. Establece que,

$\frac{d}{dx}\int^{h(x)}_{g(x)}f(s)ds = \frac{d}{dx}[F(h(x)) - F(g(x))] \\ = F'(h(x))h'(x) - F'(g(x))g'(x) \\ = f((h(x))h'(x) - f(g(x))g'(x)$

Aquí, f(t) = cos(t), h(x) = x ³ y g(x) = 0

$\frac{d}{dx}(\int^{x^3}_0cos(t)dt= cos((h(x))h'(x) - cos(g(x))g'(x) \\ = \frac{d}{dx}(\int^{x^3}_0cos(t)dt = cos(x^3)(3x^2) - cos(0)(0) \\ = \frac{d}{dx}(\int^{x^3}_0cos(t)dt) = 3x^2cos(x^3)$

Pregunta 5: Dada la siguiente función F(x), calcula su derivada.

F(x) = $\int_{0}^{sin(x)}(t + 2)dt$

Solución:

Dado: F(x) = $\int_{0}^{sin(x)}(t + 2)dt$

$\frac{d}{dx}(F(x)) = \frac{d}{dx}(\int_{0}^{sin(x)}(t + 2)dt)$

Esto se puede resolver usando la forma generalizada del teorema fundamental del cálculo parte – I. Establece que,

$\frac{d}{dx}\int^{h(x)}_{g(x)}f(s)ds = \frac{d}{dx}[F(h(x)) - F(g(x))] \\ = F'(h(x))h'(x) - F'(g(x))g'(x) \\ = f((h(x))h'(x) - f(g(x))g'(x)$

Aquí, f(t) = t + 2, g(x) = 0 y h(x) = sin(x)

$\frac{d}{dx}(\int^{sin(x)}_0(t + 2)dt)= (h(x) + 2)h'(x) - (g(x)+2)g'(x) \\ = \frac{d}{dx}(\int^{sin(x)}_0(t + 2)dt) = (sin(x) + 2)(cos(x)) - (0 + 2)(0) \\ = \frac{d}{dx}(\int^{sin(x)}_0(t + 2)dt) = cos(x)(sin(x) + 2)$

Pregunta 6: Dada la siguiente función F(x), calcula su derivada.

F(x) = $\int_{0}^{cos(x)}(t)dt$

Solución:

Dado: F(x) = $\int_{0}^{cos(x)}(t)dt$

$\frac{d}{dx}(F(x)) = \frac{d}{dx}(\int_{0}^{cos(x)}tdt)$

Esto se puede resolver usando la forma generalizada del teorema fundamental del cálculo parte – I. Establece que,

$\frac{d}{dx}\int^{h(x)}_{g(x)}f(s)ds = \frac{d}{dx}[F(h(x)) - F(g(x))] \\ = F'(h(x))h'(x) - F'(g(x))g'(x) \\ = f((h(x))h'(x) - f(g(x))g'(x)$

Aquí, f(t) = t, g(x) = 0 y h(x) = cos(x)

$\frac{d}{dx}(\int^{cos(x)}_0tdt)= (h(x))h'(x) - (g(x))g'(x) \\ = \frac{d}{dx}(\int^{cos(x)}_0tdt) = (cos(x))(-sin(x)) - (0)(0) \\ = \frac{d}{dx}(\int^{cos(x)}_0tdt) = -cos(x)sin(x)$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Aplicando el Teorema Fundamental del Cálculo

Aplicando el teorema fundamental con la regla de la string

Problemas de muestra

Deja una respuesta Cancelar la respuesta