Dado un número n , necesitamos encontrar la suma de sus dígitos tal que:
If n < 10
digSum(n) = n
Else
digSum(n) = Sum(digSum(n))
Ejemplos:
Input : 1234
Output : 1
Explanation : The sum of 1+2+3+4 = 10,
digSum(x) == 10
Hence ans will be 1+0 = 1
Input : 5674
Output : 4
Un enfoque de fuerza bruta es sumar todos los dígitos hasta que la suma < 10.
Diagrama de flujo:
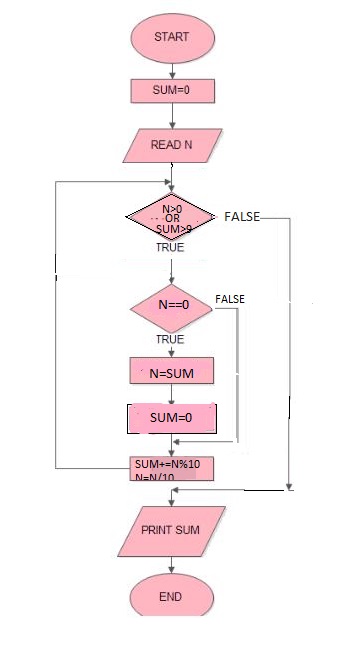
A continuación se muestra el programa de fuerza bruta para encontrar la suma.
C++
// C++ program to find sum of
// digits of a number until
// sum becomes single digit.
#include<bits/stdc++.h>
using namespace std;
int digSum(int n)
{
int sum = 0;
// Loop to do sum while
// sum is not less than
// or equal to 9
while(n > 0 || sum > 9)
{
if(n == 0)
{
n = sum;
sum = 0;
}
sum += n % 10;
n /= 10;
}
return sum;
}
// Driver program to test the above function
int main()
{
int n = 1234;
cout << digSum(n);
return 0;
}
Java
// Java program to find sum of
// digits of a number until
// sum becomes single digit.
import java.util.*;
public class GfG {
static int digSum(int n)
{
int sum = 0;
// Loop to do sum while
// sum is not less than
// or equal to 9
while (n > 0 || sum > 9)
{
if (n == 0) {
n = sum;
sum = 0;
}
sum += n % 10;
n /= 10;
}
return sum;
}
// Driver code
public static void main(String argc[])
{
int n = 1234;
System.out.println(digSum(n));
}
}
// This code is contributed by Gitanjali.
Python
# Python program to find sum of # digits of a number until # sum becomes single digit. import math # method to find sum of digits # of a number until sum becomes # single digit def digSum( n): sum = 0 while(n > 0 or sum > 9): if(n == 0): n = sum sum = 0 sum += n % 10 n /= 10 return sum # Driver method n = 1234 print (digSum(n)) # This code is contributed by Gitanjali.
C#
// C# program to find sum of
// digits of a number until
// sum becomes single digit.
using System;
class GFG {
static int digSum(int n)
{
int sum = 0;
// Loop to do sum while
// sum is not less than
// or equal to 9
while (n > 0 || sum > 9)
{
if (n == 0)
{
n = sum;
sum = 0;
}
sum += n % 10;
n /= 10;
}
return sum;
}
// Driver code
public static void Main()
{
int n = 1234;
Console.Write(digSum(n));
}
}
// This code is contributed by nitin mittal
PHP
<?php
// PHP program to find sum of
// digits of a number until
// sum becomes single digit.
function digSum( $n)
{
$sum = 0;
// Loop to do sum while
// sum is not less than
// or equal to 9
while($n > 0 || $sum > 9)
{
if($n == 0)
{
$n = $sum;
$sum = 0;
}
$sum += $n % 10;
$n = (int)$n / 10;
}
return $sum;
}
// Driver Code
$n = 1234;
echo digSum($n);
// This code is contributed
// by aj_36
?>
Javascript
<script>
// Javascript program to find sum of
// digits of a number until
// sum becomes single digit.
let n = 1234;
//Function to get sum of digits
function getSum(n) {
let sum = 0;
while (n > 0 || sum > 9) {
if(n == 0) {
n = sum;
sum = 0;
}
sum = sum + n % 10;
n = Math.floor(n / 10);
}
return sum;
}
//function call
document.write(getSum(n));
//This code is contributed by Surbhi Tyagi
</script>
C
// C program to find sum of
// digits of a number until
// sum becomes single digit.
#include<stdio.h>
int digSum(int n)
{
int sum = 0;
// Loop to do sum while
// sum is not less than
// or equal to 9
while(n > 0 || sum > 9)
{
if(n == 0)
{
n = sum;
sum = 0;
}
sum += n % 10;
n /= 10;
}
return sum;
}
// Driver program to test the above function
int main()
{
int n = 1234;
printf("%d",digSum(n));
return 0;
}
Producción :
1
Complejidad temporal: O(log(n)).
Espacio Auxiliar: O(1)
Entonces, otro desafío es «¿Podrías hacerlo sin ningún bucle/recurrencia en el tiempo de ejecución de O(1)?»
¡¡SÍ!!
También existe una solución O(1) simple y elegante para esto. La respuesta se da simplemente: –
If n == 0
return 0;
If n % 9 == 0
digSum(n) = 9
Else
digSum(n) = n % 9
¿Cómo funciona la lógica anterior?
La lógica detrás de este enfoque es:
Para verificar si un número es divisible por 9, suma los dígitos del número y verifica si la suma es divisible por 9 o no. Si es así, el número es divisible por 9, de lo contrario, no lo es.
tomemos 27, es decir (2+7 = 9), por lo tanto, divisible por 9.
Si un número n es divisible por 9, entonces la suma de su dígito hasta que la suma se convierte en un solo dígito siempre es 9. Por ejemplo,
Let, n = 2880
Suma de dígitos = 2 + 8 + 8 = 18: 18 = 1 + 8 = 9
Por lo tanto,
un número puede ser de la forma 9x o 9x + k. Para el primer caso, la respuesta siempre es 9. Para el segundo caso, siempre es k, que es el resto que queda.
El problema es ampliamente conocido como el problema de la raíz numérica.
Puede encontrar útil este artículo de Wikipedia. -> https://en.wikipedia.org/wiki/Digital_root
A continuación se muestra la implementación de la idea anterior:
C++
#include<bits/stdc++.h>
using namespace std;
int digSum(int n)
{
if (n == 0)
return 0;
return (n % 9 == 0) ? 9 : (n % 9);
}
// Driver program to test the above function
int main()
{
int n = 9999;
cout<<digSum(n);
return 0;
}
Java
import java.io.*;
class GFG {
static int digSum(int n)
{
if (n == 0)
return 0;
return (n % 9 == 0) ? 9 : (n % 9);
}
// Driver program to test the above function
public static void main (String[] args)
{
int n = 9999;
System.out.println(digSum(n));
}
}
// This code is contributed by anuj_67.
Python3
def digSum(n): if (n == 0): return 0 if (n % 9 == 0): return 9 else: return (n % 9) # Driver program to test the above function n = 9999 print(digSum(n)) # This code is contributed by # Smitha Dinesh Semwal
C#
using System;
class GFG
{
static int digSum(int n)
{
if (n == 0)
return 0;
return (n % 9 == 0) ? 9 : (n % 9);
}
// Driver Code
public static void Main ()
{
int n = 9999;
Console.Write(digSum(n));
}
}
// This code is contributed by aj_36
PHP
<?php
function digSum($n)
{
if ($n == 0)
return 0;
return ($n % 9 == 0) ? 9 : ($n % 9);
}
// Driver program to test the above function
$n = 9999;
echo digSum($n);
//This code is contributed by anuj_67.
?>
Javascript
<script>
function digSum(n)
{
if (n == 0)
return 0;
return (n % 9 == 0) ? 9 : (n % 9);
}
// Driver code
n = 9999;
document.write(digSum(n));
// This code is contributed by code_hunt
</script>
Producción:
9
Complejidad de tiempo: O(1)
Espacio Auxiliar: O(1)
Publicación relacionada:
https://www.geeksforgeeks.org/digital-rootrepeated-digital-sum-given-integer/
Este artículo es una contribución de Ayush Khanduri . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA