Encuentra el número de palabras de X vocales y Y consonantes que se pueden formar a partir de M vocales y N consonantes

Dados cuatro enteros X , Y , M y N. La tarea es encontrar el número de formas de formar una palabra eligiendo X número de vocales e Y número de consonantes del número total de M vocales y N consonantes.
Ejemplos:

Entrada: X = 2, Y = 2, M = 3, N = 3
Salida: 216
El número total de formas de elegir 2 vocales de un número total de 3 vocales es $3\choose2$ ie 3
El número total de formas de elegir 2 consonantes de un el número total de 3 consonantes es $3\choose2$ ie 3.
El número total de formas de seleccionar 2 consonantes de 3 y 2 vocales de 3 es $3\choose2$ * $3\choose2$ = 9
El número total de formas de ordenar 4 letras entre sí = 4! = 24
Por lo tanto, el número requerido de vías = 24 * 9 = 216
Entrada: X = 1, Y = 2, M = 2, N = 3
Salida: 36

El número total de formas de elegir X vocales de un número total de M vocales es $M\choose X$
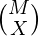
El número total de formas de elegir Y consonantes de un número total de N consonantes es $N\choose Y$
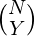
El número total de formas de seleccionar Y consonantes de N y X vocales de M es $N\choose Y$ * $M\choose X$
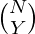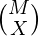
¡El número total de formas de ordenar (X+Y) las letras entre sí = (X+Y)!
Por lo tanto, el número requerido de vías = (X+Y)! * $N\choose Y$ * $M\choose X$

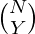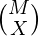
A continuación se muestra la implementación del enfoque anterior:

C++

// CPP program to find the number of words
// of X vowels  and Y consonants can be
// formed from M vowels and N consonants
#include <bits/stdc++.h>
using namespace std;
 
// Function to returns factorial of n
int fact(int n)
{
    int res = 1;
    for (int i = 2; i <= n; i++)
        res = res * i;
    return res;
}
 
// Function to find nCr
int nCr(int n, int r)
{
    return fact(n) / (fact(r) * fact(n - r));
}
 
// Function to find the number of words
// of X vowels  and Y consonants can be
// formed from M vowels and N consonants
int NumberOfWays(int X, int Y, int M, int N)
{
    return fact(X + Y) * nCr(M, X) * nCr(N, Y);
}
 
// Driver code
int main()
{
    int X = 2, Y = 2, M = 3, N = 3;
 
    // Function call
    cout << NumberOfWays(X, Y, M, N);
 
    return 0;
}

Java

// Java program to find the number of words
// of X vowels and Y consonants can be
// formed from M vowels and N consonants
import java.util.*;
import java.lang.*;
import java.io.*;
 
class GFG
{
     
    // Function to returns factorial of n
    static int fact(int n)
    {
        int res = 1;
        for (int i = 2; i <= n; i++)
            res = res * i;
        return res;
    }
     
    // Function to find nCr
    static int nCr(int n, int r)
    {
        return fact(n) / (fact(r) *
                          fact(n - r));
    }
     
    // Function to find the number of words
    // of X vowels and Y consonants can be
    // formed from M vowels and N consonants
    static int NumberOfWays(int X, int Y,
                            int M, int N)
    {
        return fact(X + Y) * nCr(M, X) *
                             nCr(N, Y);
    }
     
     
    // Driver code
    public static void main (String[] args)
                  throws java.lang.Exception
    {
        int X = 2, Y = 2, M = 3, N = 3;
     
        // Function call
        System.out.println(NumberOfWays(X, Y, M, N));        
    }
}
 
// This code is contributed by Nidhiva

Python3

# Python 3 program to find the number of words
# of X vowels and Y consonants can be
# formed from M vowels and N consonants
 
# Function to returns factorial of n
def fact(n):
    res = 1
    for i in range(2, n + 1, 1):
        res = res * i
    return res
 
# Function to find nCr
def nCr(n, r):
    return fact(n) // (fact(r) * fact(n - r))
 
# Function to find the number of words
# of X vowels and Y consonants can be
# formed from M vowels and N consonants
def NumberOfWays(X, Y, M, N):
    return fact(X + Y) * nCr(M, X) * nCr(N, Y)
 
# Driver code
if __name__ == '__main__':
    X = 2
    Y = 2
    M = 3
    N = 3
 
    # Function call
    print(NumberOfWays(X, Y, M, N))
 
# This code is contributed by
# Surendra_Gangwar

C#

// C# program to find the number of words
// of X vowels and Y consonants can be
// formed from M vowels and N consonants
using System;
 
class GFG
{
     
    // Function to returns factorial of n
    static int fact(int n)
    {
        int res = 1;
        for (int i = 2; i <= n; i++)
            res = res * i;
        return res;
    }
     
    // Function to find nCr
    static int nCr(int n, int r)
    {
        return fact(n) / (fact(r) *
                          fact(n - r));
    }
     
    // Function to find the number of words
    // of X vowels and Y consonants can be
    // formed from M vowels and N consonants
    static int NumberOfWays(int X, int Y,
                            int M, int N)
    {
        return fact(X + Y) * nCr(M, X) *
                             nCr(N, Y);
    }
     
    // Driver code
    public static void Main (String[] args)
    {
        int X = 2, Y = 2, M = 3, N = 3;
     
        // Function call
        Console.WriteLine(NumberOfWays(X, Y, M, N));        
    }
}
 
// This code is contributed by 29AjayKumar

Javascript

<script>
      // JavaScript program to find the number of words
      // of X vowels and Y consonants can be
      // formed from M vowels and N consonants
 
      // Function to returns factorial of n
      function fact(n) {
        var res = 1;
        for (var i = 2; i <= n; i++)
            res = res * i;
        return res;
      }
 
      // Function to find nCr
      function nCr(n, r) {
        return fact(n) / (fact(r) * fact(n - r));
      }
 
      // Function to find the number of words
      // of X vowels and Y consonants can be
      // formed from M vowels and N consonants
      function NumberOfWays(X, Y, M, N) {
        return fact(X + Y) * nCr(M, X) * nCr(N, Y);
      }
 
      // Driver code
      var X = 2,
        Y = 2,
        M = 3,
        N = 3;
         
      // Function call
      document.write(NumberOfWays(X, Y, M, N));
       
      // This code is contributed by rdtank.
    </script>

Producción:

Complejidad de tiempo: O(n), tiempo para calcular el factorial de n
Espacio auxiliar: O(1), ya que no se requiere espacio extra

Publicación traducida automáticamente

Artículo escrito por nidhiva y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta