Encuentre el número de segmentos que cubren cada punto en una array dada

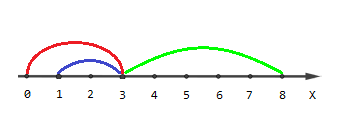
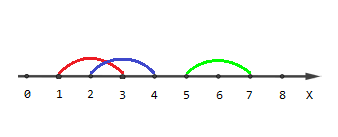
Dados los segmentos y algunos puntos, para cada punto encuentre el número de segmentos que cubren ese punto.

Un segmento (l, r) cubre un punto x si y solo si l < = x < = r .

Ejemplos: 

Entrada: Segmentos = {{0, 3}, {1, 3}, {3, 8}}, 
Puntos = {-1, 3, 8}.
Salida: {0, 3, 1}
Explicación:
 

 

• No hay segmentos que pasen por el punto -1
• Todos los segmentos que pasan por el punto 3
• Tramo 3 que pasa por el punto 8

Entrada: Segmentos = {{1, 3}, {2, 4}, {5, 7}}, 
Puntos = {0, 2, 5}.
Salida: {0, 2, 1}
Explicación:
 

 

• No hay segmentos que pasen por el punto 0
• 1er y 2do segmento que pasa por el punto 2
• Tramo 3 que pasa por el punto 5

Acercarse:

• Podemos hacer esto usando una lógica similar a la suma de prefijos.
• Representemos un segmento con (l, r). Forme un vector de pares, para cada segmento empuje dos pares en vector con valores (l, +1) y (r + 1, -1).
• Ordene los puntos en orden ascendente, pero también necesitamos su posición, así que mapéelo con su posición.
• Ordene el vector de segmento en orden descendente porque lo iteramos desde atrás.
• Realice un recuento variable de segmentos, que inicialmente es cero.
• Luego, iteraremos en el punto y sacaremos el par del vector de segmento hasta que su primer valor sea menor que el punto actual y agregaremos su segundo valor al conteo.
• Finalmente, almacene los valores de count en una array en su posición respectiva e imprima la array.

A continuación se muestra la implementación del enfoque anterior. 

// C++ program to find the number of
// segments covering each points
#include<bits/stdc++.h>
using namespace std;
 
// Function to print an array
void PrintArray(int n,int arr[])
{
     for(int i = 0; i < n; i++)
     {
         cout<<arr[i]<<" ";
     }
}
 
// Function prints number of segments
// covering by each points
void NumberOfSegments(vector<pair<int,int> >segments,
                      vector<int>points, int s, int p)
{
   vector< pair<int, int> >pts, seg;
     
   // Pushing points and index in
   // vector as a pairs
   for(int i = 0; i < p; i++)
   {
      pts.push_back({points[i], i});;
   }
     
   for(int i = 0; i < s; i++)
   {
      // (l,+1)
      seg.push_back({segments[i].first, 1});
      // (r+1,-1)
      seg.push_back({segments[i].second+1, -1});
   }
     
   // Sort the vectors
   sort(seg.begin(), seg.end(),
        greater<pair<int,int>>());
   sort(pts.begin(),pts.end());
     
   int count = 0;
   int ans[p];
     
   for(int i = 0; i < p; i++)
   {
        int x = pts[i].first;
        
        while(!seg.empty() &&
              seg.back().first <= x)
        {
            count+= seg.back().second;
            seg.pop_back();
        }
        ans[pts[i].second] = count;
   }
     
   // Print the answer
   PrintArray(p, ans);
   
}
 
//Driver code
int main()
{
  // Initializing vector of pairs
  vector<pair<int,int>>seg;
     
  // Push segments
  seg.push_back({0, 3});
  seg.push_back({1, 3});
  seg.push_back({3, 8});
     
  // Given points
  vector<int>point{-1, 3, 7};
     
  int s = seg.size();
  int p = point.size();
     
  NumberOfSegments(seg, point, s, p);
     
  return 0;
}

// Java program to find the number of 
// segments covering each points
import java.util.*;
import java.lang.*;
 
class GFG{
  
// Function to print an array
static void PrintArray(int n,int arr[])
{
    for(int i = 0; i < n; i++)
    {
        System.out.print(arr[i] + " ");
    }
}
 
// Function prints number of segments
// covering by each points
static void NumberOfSegments(ArrayList<int[]> segments,
                         int[] points, int s, int p)
{
    ArrayList<int[]> pts = new ArrayList<>(),
                     seg = new ArrayList<>();
     
    // Pushing points and index in
    // vector as a pairs
    for(int i = 0; i < p; i++)
    {
        pts.add(new int[]{points[i], i});
    }
     
    for(int i = 0; i < s; i++)
    {
        // (l,+1)
        seg.add(new int[]{segments.get(i)[0], 1});
         
        // (r+1,-1)
        seg.add(new int[]{segments.get(i)[1] + 1, -1});
    }
     
    // Sort the vectors
    Collections.sort(seg, (a, b) -> b[0] - a[0]);
    Collections.sort(pts, (a, b) -> a[0] - b[0]);
     
    int count = 0;
    int[] ans = new int[p];
     
    for(int i = 0; i < p; i++)
    {
        int x = pts.get(i)[0];
         
        while (seg.size() != 0 &&
               seg.get(seg.size() - 1)[0] <= x)
        {
            count += seg.get(seg.size() - 1)[1];
            seg.remove(seg.size() - 1);
        }
        ans[pts.get(i)[1]] = count;
    }
     
    // Print the answer
    PrintArray(p, ans);
}
 
// Driver code
public static void main(String[] args)
{
     
    // Initializing vector of pairs
    ArrayList<int[]>seg = new ArrayList<>();
     
    // Push segments
    seg.add(new int[]{0, 3});
    seg.add(new int[]{1, 3});
    seg.add(new int[]{3, 8});
     
    // Given points
    int[] point = {-1, 3, 7};
     
    int s = seg.size();
    int p = point.length;
     
    NumberOfSegments(seg, point, s, p);
}
}
 
// This code is contributed by offbeat

# Python3 program to find the number
# of segments covering each point
 
# Function to print an array
def PrintArray(n, arr):
     
    for i in range(n):
        print(arr[i], end = " ")
 
# Function prints number of segments
# covering by each points
def NumberOfSegments(segments, points, s, p):
     
    pts = []
    seg = []
     
    # Pushing points and index in
    # vector as a pairs
    for i in range(p):
        pts.append([points[i], i])
 
    for i in range(s):
         
        # (l, +1)
        seg.append([segments[i][0], 1])
         
        # (r+1, -1)
        seg.append([segments[i][1] + 1, -1])
 
    # Sort the vectors
    seg.sort(reverse = True)
    pts.sort(reverse = False)
     
    count = 0
    ans = [0 for i in range(p)]
 
    for i in range(p):
        x = pts[i][0]
 
        while(len(seg) != 0 and
          seg[len(seg) - 1][0] <= x):
                   
            count += seg[len(seg) - 1][1]
            seg.remove(seg[len(seg) - 1])
             
        ans[pts[i][1]] = count
         
    # Print the answer
    PrintArray(p, ans)
 
# Driver code
if __name__ == '__main__':
     
    # Initializing vector of pairs
    seg = []
 
    # Push segments
    seg.append([ 0, 3 ])
    seg.append([ 1, 3 ])
    seg.append([ 3, 8 ])
         
    # Given points
    point = [ -1, 3, 7 ]
         
    s = len(seg)
    p = len(point)
         
    NumberOfSegments(seg, point, s, p)
 
# This code is contributed by Bhupendra_Singh

<script>
 
// JavaScript program to find the number of
// segments covering each points
 
// Function to print an array
function PrintArray(n,arr)
{
    for(let i = 0; i < n; i++)
    {
        document.write(arr[i]," ");
    }
}
 
// Function prints number of segments
// covering by each points
function NumberOfSegments(segments,points,s,p)
{
let pts = [];
let seg = [];
     
// Pushing points and index in
// vector as a pairs
for(let i = 0; i < p; i++)
{
    pts.push([points[i], i]);
}
     
for(let i = 0; i < s; i++)
{
    // (l,+1)
    seg.push([segments[i][0], 1]);
    // (r+1,-1)
    seg.push([segments[i][1]+1, -1]);
}
     
// Sort the vectors
 
seg.sort((a,b) => b[0]-a[0]);
pts.sort((a,b) => a[0]-b[0]);
     
let count = 0;
let ans = new Array(p);
     
for(let i = 0; i < p; i++)
{
        let x = pts[i][0];
         
        while(seg.length>0 && seg[seg.length-1][0] <= x)
        {
            count+= seg[seg.length-1][1];
            seg.pop();
        }
        ans[pts[i][1]] = count;
}
     
// Print the answer
PrintArray(p, ans);
 
}
 
// Driver code
 
// Initializing vector of pairs
let seg = [];
     
// Push segments
seg.push([0, 3]);
seg.push([1, 3]);
seg.push([3, 8]);
     
// Given points
let point = [-1, 3, 7];
     
let s = seg.length;
let p = point.length;
     
NumberOfSegments(seg, point, s, p);
 
// This code is contributed by shinjanpatra.
</script>

0 3 1

Complejidad temporal: O(s*log(s) + p*log(p)), donde s es el número de segmentos yp es el número de puntos.
Espacio Auxiliar: O(s + p).