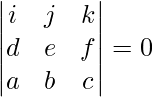Hallar la ecuación del plano que pasa por dos puntos y es paralelo a un eje dado

Dados dos puntos A(x1, y1, z1) y B(x2, y2, z2) y un conjunto de puntos (a, b, c) que representan el eje (ai + bj + ck) , la tarea es encontrar el ecuación del plano que pasa por los puntos A y B dados y paralelo al eje dado.

Ejemplos:

Entrada: x1 = 1, y1 = 2, z1 = 3, x2 = 3, y2 = 4, z2 = 5, a= 6, b = 7, c = 8
Salida: 2x + 4y + 2z + 0 = 0

Entrada: x1 = 2, y1 = 3, z1 = 5, x2 = 6, y2 = 7, z2 = 8, a= 11, b = 23, c = 10.
Salida: -29x + 7y + 48z + 0= 0

Enfoque:
A partir de los dos puntos dados en el plano A y B, las direcciones proporcionen una ecuación vectorial de la línea AB está dada por:

relación de dirección = (x2 – x1, y2 – y1, z2 – z1)

$\overrightarrow{AB} = (x2-x1) i + (y2-y1) j + (z2 - z1) k$

Desde la linea

$\overrightarrow{AB}$

es paralelo al eje dado

$(ai + bj + ck)$

. Por lo tanto, el producto cruz de

$\overrightarrow{AB}$

$(ai + bj + ck)$

es 0 que viene dado por:

$\begin{vmatrix} i & j & k\\ d & e & f \\ a & b & c \end{vmatrix} = 0$

donde,
d, e y f son el coeficiente de la ecuación vectorial de la línea AB, es decir,
d = (x2 – x1),
e = (y2 – y1) y
f = (z2 – z1)
y a, b y c son el coeficiente del eje dado.

La ecuación formada por el determinante anterior viene dada por:

$(b*f - c*e) i - (a * f - c * d) j + (a * e - b * d) k = 0$

(Ecuación 1)

La ecuación 1 es perpendicular a la línea AB , lo que significa que es perpendicular al plano requerido.
Deje que la Ecuación del plano esté dada por
$Ax + By + Cz = D$
(Ecuación 2)
donde A, B y C son la relación de dirección del plano perpendicular al plano.
Dado que la Ecuación 1 es la Ecuación 2 son perpendiculares entre sí, por lo tanto, el valor de la relación de dirección de la Ecuación 1 y 2 son paralelos. Entonces el coeficiente del plano viene dado por:

A = (b*f – c*e),
B = (a*f – c*d) y
C = (a*e – b*d)

Ahora el producto escalar del plano y la línea vectorial AB da el valor de D como

re = -(A * re – segundo * mi + C * f)

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ implementation to find the
// equation of plane which passes
// through two points and parallel
// to a given axis
 
#include <bits/stdc++.h>
using namespace std;
 
void findEquation(int x1, int y1, int z1,
                  int x2, int y2, int z2,
                  int d, int e, int f)
{
 
    // Find direction vector
    // of points (x1, y1, z1)
    // and (x2, y2, z2)
    double a = x2 - x1;
    double b = y2 - y1;
    double c = z2 - z1;
 
    // Values that are calculated
    // and simplified from the
    // cross product
    int A = (b * f - c * e);
    int B = (a * f - c * d);
    int C = (a * e - b * d);
    int D = -(A * d - B * e + C * f);
 
    // Print the equation of plane
    cout << A << "x + " << B << "y + "
         << C << "z + " << D << "= 0";
}
 
// Driver Code
int main()
{
 
    // Point A
    int x1 = 2, y1 = 3, z1 = 5;
 
    // Point B
    int x2 = 6, y2 = 7, z2 = 8;
 
    // Given axis
    int a = 11, b = 23, c = 10;
 
    // Function Call
    findEquation(x1, y1, z1,
                 x2, y2, z2,
                 a, b, c);
 
    return 0;
}

Java

// Java implementation to find the
// equation of plane which passes
// through two points and parallel
// to a given axis
import java.util.*;
 
class GFG{
 
static void findEquation(int x1, int y1, int z1,
                         int x2, int y2, int z2,
                         int d, int e, int f)
{
     
    // Find direction vector
    // of points (x1, y1, z1)
    // and (x2, y2, z2)
    double a = x2 - x1;
    double b = y2 - y1;
    double c = z2 - z1;
 
    // Values that are calculated
    // and simplified from the
    // cross product
    int A = (int)(b * f - c * e);
    int B = (int)(a * f - c * d);
    int C = (int)(a * e - b * d);
    int D = -(int)(A * d - B * e + C * f);
 
    // Print the equation of plane
    System.out.println(A + "x + " + B + "y + " +
                       C + "z + " + D + "= 0 ");
}
 
// Driver code
public static void main(String[] args)
{
 
    // Point A
    int x1 = 2, y1 = 3, z1 = 5;
 
    // Point B
    int x2 = 6, y2 = 7, z2 = 8;
 
    // Given axis
    int a = 11, b = 23, c = 10;
 
    // Function Call
    findEquation(x1, y1, z1,
                 x2, y2, z2,
                 a, b, c);
}
}
 
// This code is contributed by Pratima Pandey

Python3

# Python3 implementation
# to find the equation
# of plane which passes
# through two points and
# parallel to a given axis
def findEquation(x1, y1, z1,
                 x2, y2, z2,
                 d, e, f):
   
    # Find direction vector
    # of points (x1, y1, z1)
    # and (x2, y2, z2)
    a = x2 - x1
    b = y2 - y1
    c = z2 - z1
 
    # Values that are calculated
    # and simplified from the
    # cross product
    A = (b * f - c * e)
    B = (a * f - c * d)
    C = (a * e - b * d)
    D = -(A * d - B *
          e + C * f)
 
    # Print the equation of plane
    print (A, "x + ", B, "y + ",
           C, "z + ", D, "= 0")
 
# Driver Code
if __name__ == "__main__":
   
    # Point A
    x1 = 2
    y1 = 3
    z1 = 5;
 
    # Point B
    x2 = 6
    y2 = 7
    z2 = 8
 
    # Given axis
    a = 11
    b = 23
    c = 10
 
    # Function Call
    findEquation(x1, y1, z1,
                 x2, y2, z2,
                 a, b, c)
 
# This code is contributed by Chitranayal

C#

// C# implementation to find the
// equation of plane which passes
// through two points and parallel
// to a given axis
using System;
class GFG{
 
static void findEquation(int x1, int y1, int z1,
                         int x2, int y2, int z2,
                         int d, int e, int f)
{
     
    // Find direction vector
    // of points (x1, y1, z1)
    // and (x2, y2, z2)
    double a = x2 - x1;
    double b = y2 - y1;
    double c = z2 - z1;
 
    // Values that are calculated
    // and simplified from the
    // cross product
    int A = (int)(b * f - c * e);
    int B = (int)(a * f - c * d);
    int C = (int)(a * e - b * d);
    int D = -(int)(A * d - B * e + C * f);
 
    // Print the equation of plane
    Console.Write(A + "x + " + B + "y + " +
                  C + "z + " + D + "= 0 ");
}
 
// Driver code
public static void Main()
{
 
    // Point A
    int x1 = 2, y1 = 3, z1 = 5;
 
    // Point B
    int x2 = 6, y2 = 7, z2 = 8;
 
    // Given axis
    int a = 11, b = 23, c = 10;
 
    // Function Call
    findEquation(x1, y1, z1,
                 x2, y2, z2,
                 a, b, c);
}
}
 
// This code is contributed by Code_Mech

Javascript

<script>
// javascript implementation to find the
// equation of plane which passes
// through two points and parallel
// to a given axis
 
    function findEquation(x1 , y1 , z1 , x2 , y2 , z2 , d , e , f)
    {
 
        // Find direction vector
        // of points (x1, y1, z1)
        // and (x2, y2, z2)
        var a = x2 - x1;
        var b = y2 - y1;
        var c = z2 - z1;
 
        // Values that are calculated
        // and simplified from the
        // cross product
        var A = parseInt( (b * f - c * e));
        var B = parseInt( (a * f - c * d));
        var C = parseInt( (a * e - b * d));
        var D = -parseInt( (A * d - B * e + C * f));
 
        // Print the equation of plane
        document.write(A + "x + " + B + "y + " + C + "z + " + D + "= 0 ");
    }
 
    // Driver code
     
        // Point A
        var x1 = 2, y1 = 3, z1 = 5;
 
        // Point B
        var x2 = 6, y2 = 7, z2 = 8;
 
        // Given axis
        var a = 11, b = 23, c = 10;
 
        // Function Call
        findEquation(x1, y1, z1, x2, y2, z2, a, b, c);
 
// This code is contributed by Rajput-Ji
</script>

Producción:

-29x + 7y + 48z + 0= 0

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por Yogesh Shukla 1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta