Encuentra la ecuación para la elipse con centro en (0,4), foco en (8,4) y vértice en (6, 7)

Las secciones cónicas, comúnmente conocidas como cónicas, se crean cuando un plano se cruza con un cono. El ángulo en el que se cruzan estas secciones determina su geometría. Por lo tanto, las secciones cónicas se clasifican en cuatro tipos: círculo, elipse, parábola e hipérbola. Cada uno de estos tipos se distingue por su conjunto único de propiedades y ecuaciones matemáticas. La elipse se explica más abajo.

Elipse

Una elipse es una sección cónica generada cuando un plano cruza un cono en un ángulo (β) menor que el ángulo recto pero mayor que el ángulo formado en el vértice del cono (α). En otros términos, se genera una elipse cuando un plano corta un cono en un ángulo β tal que α<β<90 ^o .

Como se ilustra en la imagen de arriba, un cono y un plano se cruzan en un ángulo que es menor que el ángulo recto pero mayor que el ángulo formado en el vértice del cono para crear una elipse como resultado de la intersección.

Ecuación de una elipse

La ecuación estándar de una elipse centrada en (h, k) con un eje mayor paralelo al eje x viene dada por:

$\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1$ ,

donde las coordenadas del vértice son (h±a, 0), las coordenadas del co-vértice son (h, k±b) y las coordenadas de los focos son (h±c, k), donde c ² = a ² – b ² .

elipse horizontales

La ecuación estándar de una elipse centrada en (h, k) con un eje mayor paralelo al eje y viene dada por:

$\frac{(x-h)^2}{b^2}+\frac{(y-k)^2}{a^2}=1$ ,

donde las coordenadas del vértice son (h, k±a), las coordenadas del co-vértice son (h±b, k) y las coordenadas de los focos son (h, k±c), donde c ² = a ² – b ² .

elipse vertical

Encuentra la ecuación para la elipse con centro en (0,4), foco en (8,4) y vértice en (6, 7).

Solución:

Para encontrar la ecuación de una elipse, necesitamos los valores a y b.

La distancia entre el centro (0, 4) y el foco (8, 4) da c.

Entonces, c ² = (8 – 0) ² + (4 – 4) ²

c2 ⁼ 64

La distancia entre el centro (0, 4) y el vértice (6, 7) da a.

Entonces, un ² = (6 – 0) ² + (7 – 4) ²

un ² = 36 + 9

un ² = 45

Ponga los valores obtenidos en la fórmula c ² = a ² – b ² para encontrar b.

b2 ⁼ 64 – 45

b ² = 19

Como las coordenadas y del centro y el foco son las mismas, la elipse se encuentra en el eje x. Entonces la ecuación es de la forma $\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1$

Por lo tanto, la ecuación requerida de la elipse es, $\frac{x^2}{45}+\frac{(y-4)^2}{19}=1$

Problemas similares

Pregunta 1. Encuentra una ecuación para la elipse que se encuentra en el eje y con centro en (0,7), longitud del eje mayor 12 unidades y longitud del eje menor 16 unidades.

Solución:

La longitud del eje mayor es, 2a = 12 => a = 6.

La longitud del eje menor es, 2b = 16 => b = 8.

Como la elipse se encuentra en el eje y, la ecuación es $\frac{(x-h)^2}{b^2}+\frac{(y-k)^2}{a^2}=1$

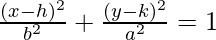
Entonces, la ecuación es $\frac{x^2}{64}+\frac{(y-7)^2}{36}=1$ .

Pregunta 2. Encuentra una ecuación para la elipse que se encuentra en el eje x con centro en (3,2), longitud del eje mayor 2 unidades y longitud del eje menor 8 unidades.

Solución:

La longitud del eje mayor es, 2a = 2 => a = 1.

La longitud del eje menor es, 2b = 8 => b = 4.

Como la elipse se encuentra en el eje x, la ecuación es $\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1$

Entonces, la ecuación es $(x-3)^2+\frac{(y-2)^2}{16}=1$ .

Pregunta 3. Encuentra las coordenadas del eje mayor de la elipse con focos (0, 6) y eje menor (8, 0).

Solución:

Tenemos, c = 6 y b = 8.

Póngalos en c ² = a ² – b ² para encontrar a.

un ² = 6 ² + 8 ²

un ² = 100

un = 10

Las coordenadas del eje mayor son (0, ±10).

Pregunta 4. Encuentra la ecuación de una elipse con centro en (7, 2) con c = 3 y b = 4.

Solución:

Dado b = 4, c = 3, h = 7 y k = 2.

Póngalos en la fórmula c ² = a ² – b ² para encontrar a.

un ² = 4 ² + 3 ²

un ² = 25

un = 5

Como la elipse se encuentra en el eje x, la ecuación es de la forma $\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1$

Entonces, la ecuación es, $\frac{(x-7)^2}{25}+\frac{(y-2)^2}{16}=1$

Pregunta 5. Encuentra la ecuación de la elipse centrada en el origen si a = 12, b = 6, y el eje menor es paralelo al eje x.

Solución:

El eje menor es paralelo al eje x, por lo que la elipse se encuentra en el eje y.

La ecuación es de la forma $\frac{(x-h)^2}{b^2}+\frac{(y-k)^2}{a^2}=1$ .

Aquí a = 12 y b = 6, h = 0 y k = 0.

Entonces, la ecuación se convierte en,

$\frac{(x-0)^2}{6^2}+\frac{(y-0)^2}{12^2}=1$

$\frac{x^2}{36}+\frac{y^2}{144}=1$

Publicación traducida automáticamente

Artículo escrito por jatinxcx y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Encuentra la ecuación para la elipse con centro en (0,4), foco en (8,4) y vértice en (6, 7).

Problemas similares

Deja una respuesta Cancelar la respuesta