Dada una array de tamaño N x M , la tarea es imprimir los elementos de la fila cuyo producto tiene un número máximo de factores primos.
Ejemplos:
Entrada: arr[][] = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
Salida: 7 8 9
Explicación:
Fila 1: (1, 2, 3) tiene producto 6 y tiene 2 factores primos.
Fila 2: (4, 5, 6) tiene producto 120 y tiene 3 factores primos.
Fila 3: (7, 8, 9) tiene producto 504 y tiene 6 factores primos.
Por lo tanto, la salida es 7 8 9, ya que tiene un número máximo de factores primos.
Entrada: arr[][] = {{11, 12, 13}, {14, 15, 16}, {17, 18, 19}}
Salida: 14 15 16
Acercarse:
- Encuentre el número total de ocurrencias de cada factor primo en cada fila recorriendo todos los elementos y encontrando sus factores primos. Usamos hashing para contar las ocurrencias.
- Sean a1, a2, …aK los recuentos de ocurrencias de factores primos . Si tenemos K factores primos distintos, entonces la respuesta será:
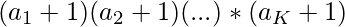
- Compare esto con el valor que almacena el recuento máximo de factores primos en una fila en max_factor . Si es mayor, actualice el valor de la fila.
- Continúe hasta que todas las filas hayan sido atravesadas.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation to find the row
// whose product has maximum number
// of prime factors
#include <bits/stdc++.h>
using namespace std;
#define N 3
#define M 5
int Large = 1e6;
vector<int> prime;
// function for SieveOfEratosthenes
void SieveOfEratosthenes()
{
// Create a boolean array "isPrime[0..N]"
// and initialize all entries it as true.
// A value in isPrime[i] will finally be
// false if i is not a prime, else true.
bool isPrime[Large + 1];
memset(isPrime, true, sizeof(isPrime));
for (int p = 2; p * p <= Large; p++) {
// check if isPrime[p] is not changed
if (isPrime[p] == true) {
// Update all multiples of p
for (int i = p * 2; i <= Large; i += p)
isPrime[i] = false;
}
}
// Print all isPrime numbers
for (int p = 2; p <= Large; p++)
if (isPrime[p])
prime.push_back(p);
}
// function to display the answer
void Display(int arr[][M], int row)
{
for (int i = 0; i < M; i++)
cout << arr[row][i] << " ";
}
// function to Count the row number of
// divisors in particular row multiplication
void countDivisorsMult(int arr[][M])
{
// Find count of occurrences
// of each prime factor
unordered_map<int, int> mp;
int row_no = 0;
long long max_factor = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
int no = arr[i][j];
for (int k = 0; k < prime.size(); k++) {
while (no > 1
&& no % prime[k] == 0) {
no /= prime[k];
mp[prime[k]]++;
}
if (no == 1)
break;
}
}
// Compute count of all divisors
long long int res = 1;
for (auto it : mp) {
res *= (it.second + 1L);
}
// Update row number if
// factors of this row is max
if (max_factor < res) {
row_no = i;
max_factor = res;
}
// Clearing map to store
// prime factors for next row
mp.clear();
}
Display(arr, row_no);
}
// Driver code
int main()
{
int arr[N][M] = { { 1, 2, 3, 10, 23 },
{ 4, 5, 6, 7, 8 },
{ 7, 8, 9, 15, 45 } };
SieveOfEratosthenes();
countDivisorsMult(arr);
return 0;
}
Java
// Java implementation to find the row
// whose product has maximum number
// of prime factors
import java.util.*;
class GFG{
static final int N = 3;
static final int M = 5;
static int Large = (int) 1e6;
static Vector<Integer> prime = new Vector<Integer>();
// function for SieveOfEratosthenes
static void SieveOfEratosthenes()
{
// Create a boolean array "isPrime[0..N]"
// and initialize all entries it as true.
// A value in isPrime[i] will finally be
// false if i is not a prime, else true.
boolean []isPrime = new boolean[Large + 1];
Arrays.fill(isPrime, true);
for (int p = 2; p * p <= Large; p++) {
// check if isPrime[p] is not changed
if (isPrime[p] == true) {
// Update all multiples of p
for (int i = p * 2; i <= Large; i += p)
isPrime[i] = false;
}
}
// Print all isPrime numbers
for (int p = 2; p <= Large; p++)
if (isPrime[p])
prime.add(p);
}
// function to display the answer
static void Display(int arr[][], int row)
{
for (int i = 0; i < M; i++)
System.out.print(arr[row][i]+ " ");
}
// function to Count the row number of
// divisors in particular row multiplication
static void countDivisorsMult(int arr[][])
{
// Find count of occurrences
// of each prime factor
HashMap<Integer,Integer> mp = new HashMap<Integer,Integer>();
int row_no = 0;
long max_factor = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
int no = arr[i][j];
for (int k = 0; k < prime.size(); k++) {
while (no > 1
&& no % prime.get(k) == 0) {
no /= prime.get(k);
if(mp.containsKey(prime.get(k)))
mp.put(prime.get(k), prime.get(k)+1);
else
mp.put(prime.get(k), 1);
}
if (no == 1)
break;
}
}
// Compute count of all divisors
int res = 1;
for (Map.Entry<Integer,Integer> it : mp.entrySet()) {
res *= (it.getValue() + 1L);
}
// Update row number if
// factors of this row is max
if (max_factor < res) {
row_no = i;
max_factor = res;
}
// Clearing map to store
// prime factors for next row
mp.clear();
}
Display(arr, row_no);
}
// Driver code
public static void main(String[] args)
{
int arr[][] = { { 1, 2, 3, 10, 23 },
{ 4, 5, 6, 7, 8 },
{ 7, 8, 9, 15, 45 } };
SieveOfEratosthenes();
countDivisorsMult(arr);
}
}
// This code is contributed by Rajput-Ji
Python3
# Python3 implementation to find the row
# whose product has maximum number
# of prime factors
N = 3
M = 5
Large = int(1e6);
prime = [];
# function for SieveOfEratosthenes
def SieveOfEratosthenes() :
# Create a boolean array "isPrime[0..N]"
# and initialize all entries it as true.
# A value in isPrime[i] will finally be
# false if i is not a prime, else true.
isPrime = [True]*(Large + 1);
for p in range(2, int(Large**(1/2))) :
# check if isPrime[p] is not changed
if (isPrime[p] == True) :
# Update all multiples of p
for i in range(p*2, Large + 1, p) :
isPrime[i] = False;
# Print all isPrime numbers
for p in range(2, Large + 1) :
if (isPrime[p]) :
prime.append(p);
# function to display the answer
def Display(arr, row) :
for i in range(M) :
print(arr[row][i], end=" ");
# function to Count the row number of
# divisors in particular row multiplication
def countDivisorsMult(arr) :
# Find count of occurrences
# of each prime factor
mp = {};
row_no = 0;max_factor = 0;
for i in range(N) :
for j in range(M) :
no = arr[i][j]
for k in range(len(prime)) :
while (no > 1 and no % prime[k] == 0) :
no //= prime[k];
if prime[k] not in mp :
mp[prime[k]] = 0
mp[prime[k]] += 1;
if (no == 1) :
break;
# Compute count of all divisors
res = 1;
for it in mp :
res *= mp[it];
# Update row number if
# factors of this row is max
if (max_factor < res) :
row_no = i;
max_factor = res;
# Clearing map to store
# prime factors for next row
mp.clear();
Display(arr, row_no);
# Driver code
if __name__ == "__main__" :
arr = [ [ 1, 2, 3, 10, 23 ],
[ 4, 5, 6, 7, 8 ],
[ 7, 8, 9, 15, 45 ] ];
SieveOfEratosthenes();
countDivisorsMult(arr);
# This code is contributed by Yash_R
C#
// C# implementation to find the row
// whose product has maximum number
// of prime factors
using System;
using System.Collections.Generic;
class GFG{
static readonly int N = 3;
static readonly int M = 5;
static int Large = (int) 1e6;
static List<int> prime = new List<int>();
// function for SieveOfEratosthenes
static void SieveOfEratosthenes()
{
// Create a bool array "isPrime[0..N]"
// and initialize all entries it as true.
// A value in isPrime[i] will finally be
// false if i is not a prime, else true.
bool []isPrime = new bool[Large + 1];
for (int p = 0; p <= Large; p++)
isPrime[p] = true;
for (int p = 2; p * p <= Large; p++)
{
// check if isPrime[p] is not changed
if (isPrime[p] == true)
{
// Update all multiples of p
for (int i = p * 2; i <= Large; i += p)
isPrime[i] = false;
}
}
// Print all isPrime numbers
for (int p = 2; p <= Large; p++)
if (isPrime[p])
prime.Add(p);
}
// function to display the answer
static void Display(int [, ]arr, int row)
{
for (int i = 0; i < M; i++)
Console.Write(arr[row, i] + " ");
}
// function to Count the row number of
// divisors in particular row multiplication
static void countDivisorsMult(int [, ]arr)
{
// Find count of occurrences
// of each prime factor
Dictionary<int,
int> mp = new Dictionary<int,
int>();
int row_no = 0;
long max_factor = 0;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
int no = arr[i,j];
for (int k = 0; k < prime.Count; k++)
{
while (no > 1 && no %
prime[k] == 0)
{
no /= prime[k];
if(mp.ContainsKey(prime[k]))
mp[prime[k]] = prime[k] + 1;
else
mp.Add(prime[k], 1);
}
if (no == 1)
break;
}
}
// Compute count of all divisors
int res = 1;
foreach (KeyValuePair<int,int> it in mp)
{
res *= (it.Value + 1);
}
// Update row number if
// factors of this row is max
if (max_factor < res)
{
row_no = i;
max_factor = res;
}
// Clearing map to store
// prime factors for next row
mp.Clear();
}
Display(arr, row_no);
}
// Driver code
public static void Main(String[] args)
{
int [, ]arr = {{1, 2, 3, 10, 23},
{4, 5, 6, 7, 8},
{7, 8, 9, 15, 45}};
SieveOfEratosthenes();
countDivisorsMult(arr);
}
}
// This code is contributed by Rajput-Ji
Javascript
<script>
// JavaScript implementation to find the row
// whose product has maximum number
// of prime factors
let N = 3
let M = 5
let Large = 1e6;
let prime = new Array();
// function for SieveOfEratosthenes
function SieveOfEratosthenes()
{
// Create a boolean array "isPrime[0..N]"
// and initialize all entries it as true.
// A value in isPrime[i] will finally be
// false if i is not a prime, else true.
let isPrime = new Array();
for(let i = 0; i < Large + 1; i++){
isPrime.push([])
}
isPrime.fill(true);
for (let p = 2; p * p <= Large; p++) {
// check if isPrime[p] is not changed
if (isPrime[p] == true) {
// Update all multiples of p
for (let i = p * 2; i <= Large; i += p)
isPrime[i] = false;
}
}
// Print all isPrime numbers
for (let p = 2; p <= Large; p++)
if (isPrime[p])
prime.push(p);
}
// function to display the answer
function Display(arr, row)
{
for (let i = 0; i < M; i++)
document.write(arr[row][i] + " ");
}
// function to Count the row number of
// divisors in particular row multiplication
function countDivisorsMult(arr)
{
// Find count of occurrences
// of each prime factor
let mp = new Map();
let row_no = 0;
let max_factor = 0;
for (let i = 0; i < N; i++) {
for (let j = 0; j < M; j++) {
let no = arr[i][j];
for (let k = 0; k < prime.length; k++) {
while (no > 1 && no % prime[k] == 0) {
no /= prime[k];
if(mp.has(prime[k])){
mp.set(prime[k], mp.get(prime[k]) + 1)
}else{
mp.set(prime[k], 1)
}
}
if (no == 1)
break;
}
}
// Compute count of all divisors
let res = 1;
for (let it of mp) {
res *= (it[1] + 1);
}
// Update row number if
// factors of this row is max
if (max_factor < res) {
row_no = i;
max_factor = res;
}
// Clearing map to store
// prime factors for next row
mp.clear();
}
Display(arr, row_no);
}
// Driver code
let arr = [ [ 1, 2, 3, 10, 23 ],
[ 4, 5, 6, 7, 8 ],
[ 7, 8, 9, 15, 45 ] ];
SieveOfEratosthenes();
countDivisorsMult(arr);
// This code is contributed by gfgking
</script>
Producción:
7 8 9 15 45