Dadas N líneas en un plano en forma de una array 2D arr[][] tal que cada fila consta de 2 enteros (digamos m & c ) donde m es la pendiente de la línea y c es la intersección con el eje y de esa línea . Se le dan consultas Q , cada una de las cuales consta de coordenadas x . La tarea es encontrar la coordenada y mínima posible correspondiente a cada línea para cada consulta.
Ejemplos:
Entrada: arr[][] = { { 4, 0 }, { -3, 0 }, { 5, 1 }, { 3, -1 },{ 2, 3 }, { 1, 4 } } y Q[ ] = {-6, 3, 100}
Salida:
-29
-9
-300
Explicación:
El valor mínimo para x = -6 del conjunto de líneas dado es -29.
El valor mínimo para x = 3 del conjunto de líneas dado es -9.
El valor mínimo para x = -100 del conjunto de líneas dado es -300.
Enfoque ingenuo: el enfoque ingenuo es encontrar las coordenadas y para cada línea y el mínimo de todas las coordenadas y dará el valor mínimo de la coordenada y. Repitiendo lo anterior para todas las consultas se obtiene la complejidad temporal de O(N*Q) .
Enfoque eficiente:
observaciones
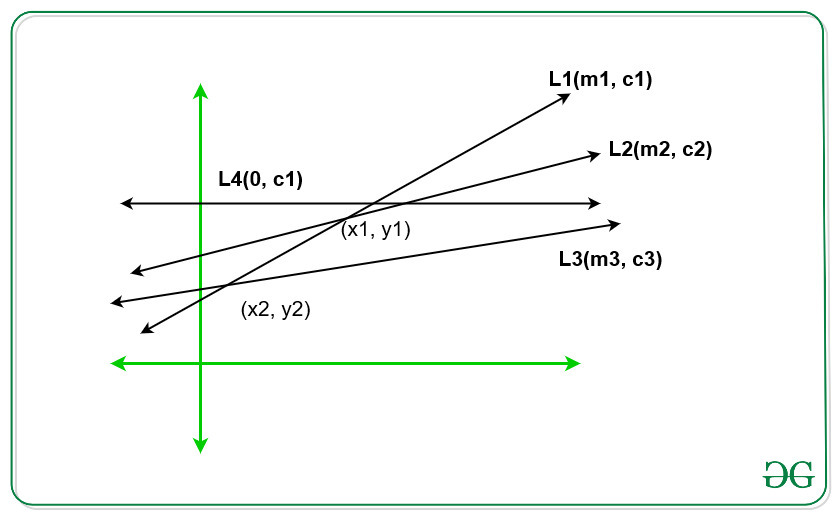
- L1 y L2 son dos líneas y se cruzan en (x1, y1) , si L1 es más bajo que antes de x = x1 , entonces L2 será más bajo que L1 después de x = x1 . Esto implica que las líneas dan un valor más bajo para algunos rangos continuos.
- L4 es la línea que es paralela al eje x, que es constante como y = c4 y nunca da el mínimo correspondiente a todas las líneas.
- Por lo tanto, la línea con pendientes más altas da un valor mínimo en las coordenadas x más bajas y un valor máximo en las coordenadas x más altas. Por ejemplo, si la pendiente (L1) > pendiente (L2) y se cruzan en (x1, y1), entonces para x < x1 , la línea L1 da el valor mínimo y para x > x1 , la línea L2 da el valor mínimo.
- Para las líneas L1, L2 y L3, si pendiente (L1) > pendiente (L2) > pendiente (L3) y si el punto de intersección de L1 y L3 está por debajo de L1 y L2 , entonces podemos ignorar la línea L2 ya que no puede dar un mínimo valor para cualquier coordenada x.
Sobre la base de las observaciones anteriores, los siguientes son los pasos:
- Ordene las pendientes en orden decreciente de pendiente.
- De un conjunto de líneas que tienen las mismas pendientes, mantenga la línea con el menor valor de intersección y y descarte todas las líneas restantes con la misma pendiente.
- Agregue las dos primeras líneas al conjunto de líneas válidas y encuentre los puntos de intersección (digamos (a, b) ).
- Para el siguiente conjunto de líneas restantes, haga lo siguiente:
- Encuentre el punto de intersección (digamos (c, d) ) de la penúltima línea y la línea actual.
- Si (c, d) es inferior a (a, b) , elimine la última línea insertada de las líneas válidas, ya que ya no es válida debido a la línea actual.
- Repita los pasos anteriores para generar todas las líneas válidas establecidas.
- Ahora tenemos un conjunto de líneas válidas y cada línea en el conjunto de líneas válidas forma el mínimo en un rango continuo en orden creciente, es decir, L1 es mínimo en el rango [a, b] y L2 en el rango [b, c] .
- Realice una búsqueda binaria en rangos [] para encontrar las coordenadas y mínimas para cada consulta de coordenadas x .
A continuación se muestra la implementación del enfoque anterior:
CPP
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// To store the valid lines
vector<pair<int, int> > lines;
// To store the distinct lines
vector<pair<int, int> > distinct;
// To store the ranges of intersection
// points
vector<pair<int, int> > ranges;
// Function that returns the intersection
// points
pair<int, int> intersection(pair<int, int> a,
pair<int, int> b)
{
int x = a.second - b.second;
int y = b.first - a.first;
return { x, y };
}
// Function to see if a line is eligible
// or not.
// L3 is the current line being added and
// we check eligibility of L2
bool isleft(pair<int, int> l1,
pair<int, int> l2,
pair<int, int> l3)
{
pair<int, int> x1, x2;
// Find intersections
x1 = intersection(l1, l3);
x2 = intersection(l1, l2);
// Returns true if x1 is left of x2
return (x1.first * x2.second
< x2.first * x1.second);
}
// Comparator function to sort the line[]
bool cmp(pair<int, int> a, pair<int, int> b)
{
if (a.first != b.first)
return a.first > b.first;
else
return a.second < b.second;
}
// Find x-coordinate of intersection
// of 2 lines
int xintersect(pair<int, int> a,
pair<int, int> b)
{
int A = a.second - b.second;
int B = b.first - a.first;
// Find the x coordinate
int x = A / B;
if (A * B < 0)
x -= 1;
return x;
}
// Function to returns the minimum
// possible value for y
int findy(vector<pair<int, int> >& ranges,
int pt)
{
int lo = 0, hi = ranges.size() - 1;
int mid = 0;
// Binary search to find the minimum
// value
while (lo <= hi) {
// Find middle element
mid = (lo + hi) / 2;
if (ranges[mid].first <= pt
&& ranges[mid].second >= pt) {
break;
}
else if (ranges[mid].first > pt) {
hi = mid - 1;
}
else {
lo = mid + 1;
}
}
// Returns the minimum value
return lines[mid].first * pt + lines[mid].second;
}
// Function to add a valid line and
// remove the invalid lines
void add(pair<int, int> x)
{
// Add the current line
lines.push_back(x);
// While Loop
while (lines.size() >= 3
&& isleft(lines[lines.size() - 3],
lines[lines.size() - 2],
lines[lines.size() - 1])) {
// Erase invalid lines
lines.erase(lines.end() - 2);
}
}
// Function to updateLines on the
// basis of distinct slopes
void updateLines(pair<int, int> line[],
int n)
{
// Sort the line according to
// decreasing order of slope
sort(line, line + n, cmp);
// To track for last slope
int lastslope = INT_MIN;
// Traverse the line[] and find
// set of distinct lines
for (int i = 0; i < n; i++) {
if (line[i].first == lastslope)
continue;
// Push the current line in
// array distinct[]
distinct.push_back(line[i]);
// Update the last slope
lastslope = line[i].first;
}
// Traverse the distinct[] and
// update the valid lines to lines[]
for (int i = 0; i < distinct.size(); i++)
add(distinct[i]);
int left = INT_MIN;
int i, right = 0;
// Traverse the valid lines array
for (i = 0; i < lines.size() - 1; i++) {
// Find the intersection point
int right = xintersect(lines[i],
lines[i + 1]);
// Insert the current intersection
// points in ranges[]
ranges.push_back({ left, right });
left = right + 1;
}
ranges.push_back({ left, INT_MAX });
}
// Driver Code
int main()
{
int n = 6;
// Set of lines of slopes and y intercept
pair<int, int> line[] = { { 4, 0 }, { -3, 0 },
{ 5, 1 }, { 3, -1 },
{ 2, 3 }, { 1, 4 } };
// Function Call
updateLines(line, n);
// Queries for x-coordinates
int Q[] = { -6, 3, 100 };
// Traverse Queries to find minimum
// y-coordinates
for (int i = 0; i < 3; i++) {
// Use Binary Search in ranges
// to find the minimum y-coordinates
cout << findy(ranges, Q[i])
<< endl;
}
return 0;
}
Python3
# Python 3 program for the above approach
# To store the valid lines
lines = []
# To store the distinct lines
distinct = []
# To store the ranges of intersection
# points
ranges = []
# Function that returns the intersection
# points
def intersection(a, b):
x = a[1] - b[1]
y = b[0] - a[0]
return x, y
# Function to see if a line is eligible
# or not.
# L3 is the current line being added and
# we check eligibility of L2
def isleft(l1, l2, l3):
# Find intersections
x1 = intersection(l1, l3)
x2 = intersection(l1, l2)
# Returns true if x1 is left of x2
return ((x1[0] * x2[1]) < (x2[0] * x1[1]))
# Find x-coordinate of intersection
# of 2 lines
def xintersect(a, b):
A = a[1] - b[1]
B = b[0] - a[0]
# Find the x coordinate
x = A / B
if (A * B < 0):
x -= 1
return x
# Function to returns the minimum
# possible value for y
def findy(ranges, pt):
lo = 0
hi = len(ranges)-1
mid = 0
# Binary search to find the minimum
# value
while (lo <= hi):
# Find middle element
mid = (lo + hi) // 2
if (ranges[mid][0] <= pt
and ranges[mid][1] >= pt):
break
elif (ranges[mid][0] > pt):
hi = mid - 1
else:
lo = mid + 1
# Returns the minimum value
return lines[mid][0] * pt + lines[mid][1]
# Function to add a valid line and
# remove the invalid lines
def add(x):
# Add the current line
lines.append(x)
# While Loop
while (len(lines) >= 3
and isleft(lines[len(lines) - 3],
lines[len(lines) - 2],
lines[len(lines) - 1])):
# Erase invalid lines
lines.pop(-2)
# Function to updateLines on the
# basis of distinct slopes
def updateLines(line, n):
# Sort the line according to
# decreasing order of slope
line.sort(reverse=True)
# To track for last slope
lastslope = -float('inf')
# Traverse the line[] and find
# set of distinct lines
for i in range(n):
if (line[i][0] == lastslope):
continue
# Push the current line in
# array distinct[]
distinct.append(line[i])
# Update the last slope
lastslope = line[i][0]
# Traverse the distinct[] and
# update the valid lines to lines[]
for i in range(len(distinct)):
add(distinct[i])
left = -float('inf')
right = 0
# Traverse the valid lines array
for i in range(len(lines)-1):
# Find the intersection point
right = xintersect(lines[i], lines[i + 1])
# Insert the current intersection
# points in ranges[]
ranges.append((left, right))
left = right + 1
ranges.append((left, float('inf')))
# Driver Code
if __name__ == '__main__':
n = 6
# Set of lines of slopes and y intercept
line = [(4, 0), (-3, 0),
(5, 1), (3, -1),
(2, 3), (1, 4)]
# Function Call
updateLines(line, n)
# Queries for x-coordinates
Q = [ -6, 3, 100]
# Traverse Queries to find minimum
# y-coordinates
for i in range(3):
# Use Binary Search in ranges
# to find the minimum y-coordinates
print(findy(ranges, Q[i]))
-29 -9 -300
Complejidad de tiempo: O(N + Q*log N) , donde N es el número de líneas y Q es el número de consultas
Espacio auxiliar: O(N)