Encuentra N fracciones que suman una fracción dada N/D

Dada una fracción N/D , la tarea es dividir esta fracción en N partes de modo que su suma sea igual a la fracción N/D, es decir,
$\frac{N}{D} = \frac{a_1}{b_1} + \frac{a_2}{b_2} + ... + \frac{a_N}{b_N}$
Nota: Representa los términos en términos de fracciones, en lugar de números de punto flotante.

Entrada: N = 4, D = 2
Salida: 4/5, 1/5, 1/3, 4/6
Explicación:
$\frac{4}{5} + \frac{1}{5} + \frac{1}{3} + \frac{4}{6} = \frac{4}{2}$
Por lo tanto, es un conjunto de fracciones válido tal que su suma es $\frac{N}{D}$

Entrada: N = 3, D = 4
Salida: 1/2, 1/10, 3/20
Explicación:
$\frac{1}{2} + \frac{1}{10} + \frac{3}{20} = \frac{3}{4}$
Por lo tanto, es un conjunto de fracciones válido tal que su suma es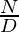 $\frac{N}{D}$

Enfoque: La observación clave en el problema es que el numerador de la primera fracción puede ser $D + N - 1$ y luego los $N-1$ denominadores adicionales pueden usar la siguiente relación de recurrencia.

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ implementation to split the
// fraction into N parts
#include<bits/stdc++.h>
using namespace std;
 
// Function to split the fraction
// into the N parts
void splitFraction(int n, int d)
{
    int ar[n];
    int first = d + n - 1;
    ar[0] = first;
 
    // Loop to find the N - 1
    // fraction
    for(int i = 1; i < n; i++)
    {
       int temp = --first;
       first++;
 
       ar[i] = first * temp;
       --first;
    }
 
    // Loop to print the Fractions
    for(int i = 0; i < n; i++)
    {
       if (ar[i] % n == 0)
       {
           cout << "1/" << ar[i] / n << ", ";
       }
       else
       {
           cout << n << "/" << ar[i] << ", ";
       }
    }
}
 
// Driver Code
int main()
{
    int N = 4;
    int D = 2;
 
    // Function Call
    splitFraction(N, D);
}
 
// This code is contributed by Bhupendra_Singh

Java

// Java implementation to split the
// fraction into N parts
 
import java.util.Scanner;
 
class Solution {
 
    // Function to split the fraction
    // into the N parts
    public static void
    splitFraction(int n, int d)
    {
 
        long ar[] = new long[n];
        long first = d + n - 1;
        ar[0] = first;
 
        // Loop to find the N - 1
        // fraction
        for (int i = 1; i < n; i++) {
            ar[i] = first * (--first);
        }
 
        // Loop to print the Fractions
        for (int i = 0; i < n; i++) {
            if (ar[i] % n == 0) {
                System.out.print(
                    "1/" + ar[i] / n
                    + ", ");
            }
            else {
                System.out.print(
                    n + "/" + ar[i]
                    + ", ");
            }
        }
    }
 
    // Driver Code
    public static void main(
        String[] args) throws Exception
    {
        int N = 4;
        int D = 2;
 
        // Function Call
        splitFraction(N, D);
    }
}

Python3

# Python3 implementation to split the
# fraction into N parts
 
# Function to split the fraction
# into the N parts
def splitFraction(n, d):
     
    ar = []
    for i in range(0, n):
        ar.append(0)
     
    first = d + n - 1
    ar[0] = first
     
    # Loop to find the N - 1
    # fraction
    for i in range(1, n):
        temp = first - 1
        ar[i] = first * temp
        first -= 1
     
    # Loop to print the Fractions
    for i in range(0, n):
        if ar[i] % n == 0:
            print("1/", int(ar[i] / n),
                  "," , end = " ")
                   
        else:
            print(n, "/", ar[i], ",", end = " ")
     
# Driver Code
N = 4
D = 2
 
# Function Call
splitFraction(N, D)
 
# This code is contributed by ishayadav181

C#

// C# implementation to split the
// fraction into N parts
using System;
 
class GFG{
 
// Function to split the fraction
// into the N parts
public static void splitFraction(int n, int d)
{
    long []ar = new long[n];
    long first = d + n - 1;
    ar[0] = first;
 
    // Loop to find the N - 1
    // fraction
    for(int i = 1; i < n; i++)
    {
       ar[i] = first * (--first);
    }
 
    // Loop to print the Fractions
    for(int i = 0; i < n; i++)
    {
       if (ar[i] % n == 0)
       {
           Console.Write("1/" + ar[i] / n + ", ");
       }
       else
       {
           Console.Write(n + "/" + ar[i] + ", ");
       }
    }
}
 
// Driver Code
public static void Main(String[] args)
{
    int N = 4;
    int D = 2;
 
    // Function Call
    splitFraction(N, D);
}
}
 
// This code is contributed by SoumikMondal

Javascript

<script>
      // JavaScript implementation to split the
      // fraction into N parts
      // Function to split the fraction
      // into the N parts
      function splitFraction(n, d) {
        var ar = new Array(n);
        var first = d + n - 1;
        ar[0] = first;
 
        // Loop to find the N - 1
        // fraction
        for (var i = 1; i < n; i++) {
          ar[i] = first * --first;
        }
 
        // Loop to print the Fractions
        for (var i = 0; i < n; i++) {
          if (ar[i] % n === 0) {
            document.write("1/" + ar[i] / n + ", ");
          } else {
            document.write(n + "/" + ar[i] + ", ");
          }
        }
      }
 
      // Driver Code
      var N = 4;
      var D = 2;
 
      // Function Call
      splitFraction(N, D);
    </script>

Producción:

4/5, 1/5, 1/3, 4/6,

Complejidad de tiempo: O(n), donde n es el número entero dado.

Espacio Auxiliar: O(n), donde n es el entero dado.

Publicación traducida automáticamente

Artículo escrito por abhinavpande y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta