Dado un número entero N. La tarea es encontrar todos los factores de N e imprimir el producto de cuatro factores de N tal que:
- La suma de los cuatro factores es igual a N.
- El producto de los cuatro factores es máximo.
Si no es posible encontrar 4 de esos factores, imprima «No es posible».
Nota : Los cuatro factores pueden ser iguales entre sí para maximizar el producto y puede haber una gran cantidad de consultas.
Ejemplos :
Input: 24 Output: Product -> 1296 All factors are -> 1 2 3 4 6 8 12 24 Choose the factor 6 four times, Therefore, 6+6+6+6 = 24 and product is maximum. Input: 100 Output: Product -> 390625 All the factors are -> 1 2 4 5 10 10 20 25 50 100 Choose the factor 25 four times.
La idea es encontrar factores de todos los números del 1 al N (que es el valor máximo de n).
- Una respuesta será No posible si lo dado
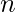es primo. - Y si el n dado es divisible por 4 entonces la respuesta será pow(q, 4) donde q es un cociente cuando n se divide por 4.
- Si es posible encontrar la respuesta entonces, la respuesta debe incluir el penúltimo factor dos veces. Y ejecute un bucle anidado para otros dos factores.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of above approach
#include <bits/stdc++.h>
using namespace std;
// Function to find primes
bool isPrime(int n)
{
// Corner cases
if (n <= 1)
return false;
if (n <= 3)
return true;
// This is checked so that we can skip
// middle five numbers in below loop
if (n % 2 == 0 || n % 3 == 0)
return false;
for (int i = 5; i * i <= n; i = i + 6)
if (n % i == 0 || n % (i + 2) == 0)
return false;
return true;
}
// Function to find factors
void factors(int N, vector<int>& v[])
{
for (int i = 2; i < N; i++) {
// run a loop upto square root of that number
for (int j = 1; j * j <= i; j++) {
if (i % j == 0) {
// if the n is perfect square
if (i / j == j)
v[i].push_back(j);
// otherwise push it's two divisors
else {
v[i].push_back(j);
v[i].push_back(i / j);
}
}
}
// sort the divisors
sort(v[i].begin(), v[i].end());
}
}
// Function to find max product
int product(int n)
{
// To store factors of 'n'
vector<int> v[n + 100];
// find factors
factors(n + 100, v);
// if it is divisible by 4.
if (n % 4 == 0) {
int x = n / 4;
x *= x;
return x * x;
}
else {
// if it is prime
if (isPrime[n])
return -1;
// otherwise answer will be possible
else {
int ans = -1;
if (v[n].size() > 2) {
// include last third factor
int fac = v[n][v[n].size() - 3];
// nested loop to find other two factors
for (int i = v[n].size() - 1; i >= 0; i--) {
for (int j = v[n].size() - 1; j >= 0; j--) {
if ((fac * 2) + (v[n][j] + v[n][i]) == n)
ans = max(ans, fac * fac * v[n][j] * v[n][i]);
}
}
return ans;
}
}
}
}
// Driver code
int main()
{
int n = 24;
// function call
cout << product(n);
return 0;
}
Java
// Java implementation of above approach
import java.util.*;
import java.lang.*;
import java.io.*;
class GFG
{
// Function to find primes
static boolean isPrime(int n)
{
// Corner cases
if (n <= 1)
return false;
if (n <= 3)
return true;
// This is checked so that we can skip
// middle five numbers in below loop
if (n % 2 == 0 || n % 3 == 0)
return false;
for (int i = 5; i * i <= n; i = i + 6)
if (n % i == 0 || n % (i + 2) == 0)
return false;
return true;
}
static Vector<Vector<Integer> > v = new Vector<Vector<Integer> >();
// Function to find factors
static void factors(int N )
{
for (int i = 2; i < N; i++)
{
// run a loop upto square root of that number
for (int j = 1; j * j <= i; j++)
{
if (i % j == 0)
{
// if the n is perfect square
if (i / j == j)
v.get(i).add(j);
// otherwise push it's two divisors
else
{
v.get(i).add(j);
v.get(i).add(i / j);
}
}
}
// sort the divisors
Collections.sort(v.get(i));
}
}
// Function to find max product
static int product(int n)
{
// To store factors of 'n'
v.clear();
for(int i = 0; i < n + 100; i++)
v.add(new Vector<Integer>());
// find factors
factors(n + 100);
// if it is divisible by 4.
if (n % 4 == 0)
{
int x = n / 4;
x *= x;
return x * x;
}
else
{
// if it is prime
if (isPrime(n))
return -1;
// otherwise answer will be possible
else
{
int ans = -1;
if (v.get(n).size() > 2)
{
// include last third factor
int fac = v.get(n).get(v.get(n).size() - 3);
// nested loop to find other two factors
for (int i = v.get(n).size() - 1; i >= 0; i--)
{
for (int j = v.get(n).size() - 1; j >= 0; j--)
{
if ((fac * 2) + (v.get(n).get(j) +
v.get(n).get(i)) == n)
ans = Math.max(ans, fac * fac *
v.get(n).get(j) *
v.get(n).get(i));
}
}
return ans;
}
}
}
return 0;
}
// Driver code
public static void main(String args[])
{
int n = 24;
// function call
System.out.println( product(n));
}
}
// This code is contributed by Arnab Kundu
Python3
# Python3 implementation of above approach from math import sqrt, ceil, floor # Function to find primes def isPrime(n): # Corner cases if (n <= 1): return False if (n <= 3): return True # This is checked so that we can skip # middle five numbers in below loop if (n % 2 == 0 or n % 3 == 0): return False for i in range(5, ceil(sqrt(n)), 6): if (n % i == 0 or n % (i + 2) == 0): return False return True # Function to find factors def factors(N, v): for i in range(2, N): # run a loop upto square root of that number for j in range(1,ceil(sqrt(i)) + 1): if (i % j == 0): # if the n is perfect square if (i // j == j): v[i].append(j) # otherwise push it's two divisors else: v[i].append(j) v[i].append(i // j) # sort the divisors v = sorted(v) # Function to find max product def product(n): # To store factors of 'n' v = [[]] * (n + 100) # find factors factors(n + 100, v) # if it is divisible by 4. if (n % 4 == 0): x = n // 4 x *= x return x * x else : # if it is prime if (isPrime[n]): return -1 # otherwise answer will be possible else : ans = -1 if (len(v[n]) > 2): # include last third factor fac = v[n][len(v[n]) - 3] # nested loop to find other two factors for i in range(len(v[n] - 1), -1, -1): for j in range(len(v[n] - 1), -1, -1): if ((fac * 2) + (v[n][j] + v[n][i]) == n): ans = max(ans, fac * fac * v[n][j] * v[n][i]) return ans # Driver code n = 24 # function call print(product(n)) # This code is contributed by mohit kumar 29
C#
// C# implementation of above approach
using System;
using System.Collections.Generic;
class GFG
{
// Function to find primes
static bool isPrime(int n)
{
// Corner cases
if (n <= 1)
return false;
if (n <= 3)
return true;
// This is checked so that we can skip
// middle five numbers in below loop
if (n % 2 == 0 || n % 3 == 0)
return false;
for (int i = 5; i * i <= n; i = i + 6)
if (n % i == 0 || n % (i + 2) == 0)
return false;
return true;
}
static List<List<int> > v = new List<List<int> >();
// Function to find factors
static void factors(int N )
{
for (int i = 2; i < N; i++)
{
// run a loop upto square root of that number
for (int j = 1; j * j <= i; j++)
{
if (i % j == 0)
{
// if the n is perfect square
if (i / j == j)
v[i].Add(j);
// otherwise push it's two divisors
else
{
v[i].Add(j);
v[i].Add(i / j);
}
}
}
// sort the divisors
v[i].Sort();
}
}
// Function to find max product
static int product(int n)
{
// To store factors of 'n'
v.Clear();
for(int i = 0; i < n + 100; i++)
v.Add(new List<int>());
// find factors
factors(n + 100);
// if it is divisible by 4.
if (n % 4 == 0)
{
int x = n / 4;
x *= x;
return x * x;
}
else
{
// if it is prime
if (isPrime(n))
return -1;
// otherwise answer will be possible
else
{
int ans = -1;
if (v[n].Count > 2)
{
// include last third factor
int fac = v[n][v[n].Count - 3];
// nested loop to find other two factors
for (int i = v[n].Count - 1; i >= 0; i--)
{
for (int j = v[n].Count - 1; j >= 0; j--)
{
if ((fac * 2) + (v[n][j] +
v[n][i]) == n)
ans = Math.Max(ans, fac * fac *
v[n][j] *
v[n][i]);
}
}
return ans;
}
}
}
return 0;
}
// Driver code
public static void Main(String []args)
{
int n = 24;
// function call
Console.WriteLine( product(n));
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// Javascript implementation of above approach
// Function to find primes
function isPrime(n) {
// Corner cases
if (n <= 1)
return false;
if (n <= 3)
return true;
// This is checked so that we can skip
// middle five numbers in below loop
if (n % 2 == 0 || n % 3 == 0)
return false;
for (let i = 5; i * i <= n; i = i + 6)
if (n % i == 0 || n % (i + 2) == 0)
return false;
return true;
}
// Function to find factors
function factors(N, v) {
for (let i = 2; i < N; i++) {
// run a loop upto square root of that number
for (let j = 1; j * j <= i; j++) {
if (i % j == 0) {
// if the n is perfect square
if (i / j == j)
v[i].push(j);
// otherwise push it's two divisors
else {
v[i].push(j);
v[i].push(i / j);
}
}
}
// sort the divisors
v.sort((a, b) => a - b);
}
}
// Function to find max product
function product(n) {
// To store factors of 'n'
let v = new Array();
for (let i = 0; i < n + 100; i++) {
v.push(new Array())
}
// find factors
factors(n + 100, v);
// if it is divisible by 4.
if (n % 4 == 0) {
let x = n / 4;
x *= x;
return x * x;
}
else {
// if it is prime
if (isPrime[n])
return -1;
// otherwise answer will be possible
else {
let ans = -1;
if (v[n].length > 2) {
// include last third factor
let fac = v[n][v[n].length - 3];
// nested loop to find other two factors
for (let i = v[n].length - 1; i >= 0; i--) {
for (let j = v[n].length - 1; j >= 0; j--) {
if ((fac * 2) + (v[n][j] + v[n][i]) == n)
ans = Math.max(ans, fac * fac * v[n][j] * v[n][i]);
}
}
return ans;
}
}
}
}
// Driver code
let n = 24;
// function call
document.write(product(n));
// This code is contributed by _saurabh_jaiswal
</script>
Producción:
1296
Publicación traducida automáticamente
Artículo escrito por pawan_asipu y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA