Encuentre el Node cuya suma con X tiene bits establecidos mínimos

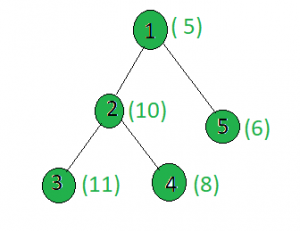
Dado un árbol, y los pesos de todos los Nodes y un entero x , la tarea es encontrar un Node i tal que peso[i] + x proporcione los bits establecidos mínimos, si dos o más Nodes tienen el mismo número de bits establecidos cuando sumado con x luego encuentra el que tiene el valor mínimo.

Ejemplos: 

Aporte: 
 

x = 15 
Salida: 1 
Node 1: setbits(5 + 15) = 2 
Node 2: setbits(10 + 15) = 3 
Node 3: setbits(11 + 15) = 3 
Node 4: setbits(8 + 15) = 4 
Node 5: conjunto de bits (6 + 15) = 3 
 

Enfoque: Realice dfs en el árbol y realice un seguimiento del Node cuya suma con x tiene bits establecidos mínimos. Si dos o más Nodes tienen la misma cantidad de bits establecidos, elija el que tenga el número mínimo.

A continuación se muestra la implementación del enfoque anterior: 

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
int minimum = INT_MAX, x, ans = INT_MAX;
 
vector<int> graph[100];
vector<int> weight(100);
 
// Function to perform dfs to find
// the minimum set bits value
void dfs(int node, int parent)
{
    // If current set bits value is smaller than
    // the current minimum
    int a = __builtin_popcount(weight[node] + x);
    if (minimum > a) {
        minimum = a;
        ans = node;
    }
 
    // If count is equal to the minimum
    // then choose the node with minimum value
    else if (minimum == a)
        ans = min(ans, node);
 
    for (int to : graph[node]) {
        if (to == parent)
            continue;
        dfs(to, node);
    }
}
 
// Driver code
int main()
{
    x = 15;
 
    // Weights of the node
    weight[1] = 5;
    weight[2] = 10;
    weight[3] = 11;
    weight[4] = 8;
    weight[5] = 6;
 
    // Edges of the tree
    graph[1].push_back(2);
    graph[2].push_back(3);
    graph[2].push_back(4);
    graph[1].push_back(5);
 
    dfs(1, 1);
 
    cout << ans;
 
    return 0;
}

// Java implementation of the approach
import java.util.*;
class GFG{
 
static int minimum = Integer.MAX_VALUE,
           x, ans = Integer.MAX_VALUE;
 
static Vector<Integer> []graph =
              new Vector[100];
static int []weight = new int[100];
 
// Function to perform dfs
// to find the minimum set
// bits value
static void dfs(int node,
                int parent)
{
  // If current set bits value
  // is smaller than the current
  // minimum
  int a = Integer.bitCount(weight[node] + x);
  if (minimum > a)
  {
    minimum = a;
    ans = node;
  }
 
  // If count is equal to the
  // minimum then choose the
  // node with minimum value
  else if (minimum == a)
    ans = Math.min(ans, node);
 
  for (int to : graph[node])
  {
    if (to == parent)
      continue;
    dfs(to, node);
  }
}
 
// Driver code
public static void main(String[] args)
{
  x = 15;
  for (int i = 0; i < graph.length; i++)
    graph[i] = new Vector<Integer>();
   
  // Weights of the node
  weight[1] = 5;
  weight[2] = 10;
  weight[3] = 11;
  weight[4] = 8;
  weight[5] = 6;
 
  // Edges of the tree
  graph[1].add(2);
  graph[2].add(3);
  graph[2].add(4);
  graph[1].add(5);
 
  dfs(1, 1);
 
  System.out.print(ans);
}
}
 
// This code is contributed by gauravrajput1

# Python3 implementation of the approach
from sys import maxsize
 
minimum, x, ans = maxsize, None, maxsize
 
graph = [[] for i in range(100)]
weight = [0] * 100
 
# Function to perform dfs to find
# the minimum set bits value
def dfs(node, parent):
    global x, ans, graph, weight, minimum
 
    # If current set bits value is greater than
    # the current minimum
    a = bin(weight[node] + x).count('1')
 
    if minimum > a:
        minimum = a
        ans = node
 
    # If count is equal to the minimum
    # then choose the node with minimum value
    elif minimum == a:
        ans = min(ans, node)
 
    for to in graph[node]:
        if to == parent:
            continue
        dfs(to, node)
 
# Driver Code
if __name__ == "__main__":
 
    x = 15
 
    # Weights of the node
    weight[1] = 5
    weight[2] = 10
    weight[3] = 11
    weight[4] = 8
    weight[5] = 6
 
    # Edges of the tree
    graph[1].append(2)
    graph[2].append(3)
    graph[2].append(4)
    graph[1].append(5)
 
    dfs(1, 1)
 
    print(ans)
 
# This code is contributed by
# sanjeev2552

// C# implementation of the approach
using System;
using System.Collections;
using System.Collections.Generic;
using System.Text;
 
class GFG{
     
static int minimum = int.MaxValue, x,
               ans = int.MaxValue;
 
static ArrayList[] graph = new ArrayList[100];
static int[] weight = new int[100];
 
static int PopCount(int n)
{
    int count = 0;
     
    while (n > 0)
    {
        count += n & 1;
        n >>= 1;
    }
    return count;
}
 
// Function to perform dfs to find
// the minimum set bits value
static void dfs(int node, int parent)
{
     
    // If current set bits value is smaller
    // than the current minimum
    int a = PopCount(weight[node] + x);
    if (minimum > a)
    {
        minimum = a;
        ans = node;
    }
 
    // If count is equal to the minimum
    // then choose the node with minimum value
    else if (minimum == a)
        ans = Math.Min(ans, node);
 
    foreach(int to in graph[node])
    {
        if (to == parent)
            continue;
             
        dfs(to, node);
    }
}
     
// Driver Code
public static void Main(string[] args)
{
    x = 15;
     
    for(int i = 0; i < 100; i++)
        graph[i] = new ArrayList();
     
    // Weights of the node
    weight[1] = 5;
    weight[2] = 10;
    weight[3] = 11;
    weight[4] = 8;
    weight[5] = 6;
 
    // Edges of the tree
    graph[1].Add(2);
    graph[2].Add(3);
    graph[2].Add(4);
    graph[1].Add(5);
 
    dfs(1, 1);
 
    Console.Write(ans);
}
}
 
// This code is contributed by rutvik_56

<script>
  
// Javascript implementation of the approach
let minimum = Number.MAX_VALUE;
let x;
let ans = Number.MAX_VALUE;
 
let graph = new Array(100);
let weight = new Array(100);
for(let i = 0; i < 100; i++)
{
    graph[i] = [];
    weight[i] = 0;
}
 
// Function to perform dfs to find
// the minimum set bits value
function dfs(node, parent)
{
     
    // If current set bits value is smaller than
    // the current minimum
    let a = (weight[node] + x).toString(2).split('').filter(
            y => y == '1').length;
    if (minimum > a)
    {
        minimum = a;
        ans = node;
    }
 
    // If count is equal to the minimum
    // then choose the node with minimum value
    else if (minimum == a)
        ans = Math.min(ans, node);
         
    for(let to = 0; to < graph[node].length; to++)
    {
        if (graph[node][to] == parent)
            continue
             
        dfs(graph[node][to], node);
    }
}
 
// Driver code
x = 15;
 
// Weights of the node
weight[1] = 5;
weight[2] = 10;
weight[3] = 11;
weight[4] = 8;
weight[5] = 6;
 
// Edges of the tree
graph[1].push(2);
graph[2].push(3);
graph[2].push(4);
graph[1].push(5);
 
dfs(1, 1);
 
document.write(ans);
 
// This code is contributed by Dharanendra L V.
  
</script>

1

Análisis de Complejidad:  

• Complejidad temporal: O(N). 
  En dfs, cada Node del árbol se procesa una vez y, por lo tanto, la complejidad debida a dfs es O(N) si hay un total de N Nodes en el árbol. Además, para procesar cada Node se usa la función builtin_popcount() que tiene una complejidad de O(c) donde c es una constante, y dado que esta complejidad es constante, no afecta la complejidad temporal general. Por lo tanto, la complejidad del tiempo es O(N).
• Espacio Auxiliar: O(1). 
  No se requiere ningún espacio adicional, por lo que la complejidad del espacio es constante.