Encuentre elementos en una array dada que sean un factor de la suma de los elementos restantes

Dada una array A[] de tamaño N , la tarea es encontrar los elementos de la array que son factores de la suma del elemento restante. Entonces simplemente seleccione un elemento de una array y tome la suma de los elementos restantes y verifique si la suma es perfectamente divisible por el elemento seleccionado o no. Si es divisible, devuelve el elemento.

Ejemplos:

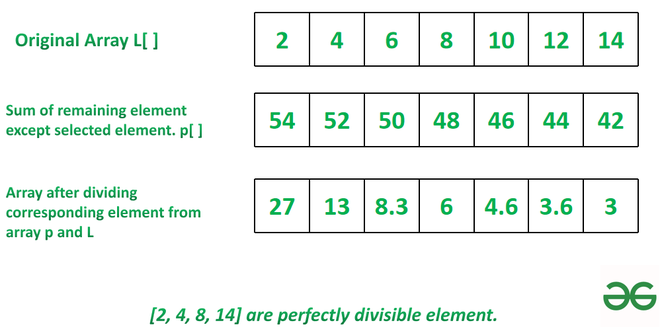
Entrada: A[] = {2, 4, 6, 8, 10, 12, 14}
Salida: [2, 4, 8, 14]
Explicación: 
1. Tome la suma del elemento restante excepto el seleccionado.
2. Para el elemento 2, la suma del elemento restante es 4+6+8+10+12+14=54 
3. De manera similar para la array completa: [54, 52, 50, 48, 46, 44, 42]
3. 54/ 2, 52/4, 48/8, 42/14 son perfectamente divisibles por lo que los elementos resultantes son [2, 4, 8, 14]

Entrada: A[]= {3, 6, 8, 10, 7, 15}
Salida: [7]

Enfoque ingenuo: tome la suma de todos los elementos de la array. Ahora reste cada elemento uno por uno de la suma y agréguelo a la nueva array p []. Divida cada suma por el elemento de índice correspondiente de una array dada y agréguelo a la nueva array q[]. Multiplique el elemento correspondiente de la array A[] y la array q[] y compárelo con elementos indexados similares de la array p[] . Si son iguales, agréguelo a una nueva array z[ ] . Si no se encuentra tal elemento, devuelve -1.

A continuación se muestra la implementación del enfoque anterior.

// c++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to find element
vector<int> Factor(vector<int> A)
{
 
  // Sum of all element
  int s = 0;
 
  for (int i = 0; i < A.size(); i++)
  {
    s += A[i];
  }
 
  // Subtract each element from sum
  vector<int> p;
  for (int i : A)
    p.push_back(s - i);
 
  // Divide corresponding element
  // from array p and l
  vector<int> q;
  for (int i = 0; i < A.size(); i++)
    q.push_back(p[i] / A[i]);
 
  // Check sum is divisible by
  // corresponding element or not
  vector<int> z;
  for (int i = 0; i < q.size(); i++)
  {
 
    // First we divided element now multiple
    // to check perfect divisibility of element
    if (q[i] * A[i] == p[i])
      z.push_back(A[i]);
  }
 
  return z;
}
 
// Driver code
int main()
{
  vector<int> A = {2, 4, 6, 8, 10, 12, 14};
 
  // Calling function
  vector<int> b = Factor(A);
 
  // Print required array
  for (auto i : b)
  {
    cout << i << " ";
  }
}
 
// This code is contributed by amreshkumar3.

// Java program for the above approach
import java.util.ArrayList;
 
class GFG{
 
// Function to find element
static ArrayList<Integer> Factor(int[] A)
{
     
    // Sum of all element
    int s = 0;
 
    for(int i = 0; i < A.length; i++)
    {
        s += A[i];
    }
 
    // Subtract each element from sum
    ArrayList<Integer> p = new ArrayList<>();
    for(int i : A)
        p.add(s - i);
 
    // Divide corresponding element
    // from array p and l
    ArrayList<Integer> q = new ArrayList<Integer>();
    for(int i = 0; i < A.length; i++)
        q.add((int) Math.floor(p.get(i) / A[i]));
 
    // Check sum is divisible by
    // corresponding element or not
    ArrayList<Integer> z = new ArrayList<Integer>();
    for(int i = 0; i < q.size(); i++)
    {
         
        // First we divided element now multiple
        // to check perfect divisibility of element
        if (q.get(i) * A[i] == p.get(i))
            z.add(A[i]);
    }
     
    // If no such element found return -1
    if (z.size() == 0)
        return new ArrayList<Integer>();
         
    return z;
}
 
// Driver code
public static void main(String args[])
{
    int[] A = { 2, 4, 6, 8, 10, 12, 14 };
 
    // Calling function
    ArrayList<Integer> b = Factor(A);
 
    // Print required array
    System.out.println(b);
}
}
 
// This code is contributed by gfgking

# Python program for the above approach
 
# Function to find element
def Factor(A):
   
    # Sum of all element
    s = sum(A)
     
    # Subtract each element from sum
    p =[]
    for i in A:
        p.append(s-i)
 
    # Divide corresponding element
    # from array p and l
    q =[]
    for i in range(len(A)):
        q.append(p[i]//A[i])
 
    # Check sum is divisible by
    # corresponding element or not
    z =[]
    for i in range(len(q)):
       
          # First we divided element now multiple
        # to check perfect divisibility of element
        if q[i]*A[i]== p[i]:
            z.append(A[i])
             
    # If no such element found return -1
    if len(z)== 0:
      return -1
    return z
 
A = [2, 4, 6, 8, 10, 12, 14]
 
# Calling function
b = Factor(A)
 
# Print required array
print(b)

// C# program for the above approach
using System;
using System.Collections.Generic;
 
public class GFG{
 
  // Function to find element
  static List<int> Factor(int[] A)
  {
 
    // Sum of all element
    int s = 0;
 
    for(int i = 0; i < A.Length; i++)
    {
      s += A[i];
    }
 
    // Subtract each element from sum
    List<int> p = new List<int>();
    foreach(int i in A)
      p.Add(s - i);
 
    // Divide corresponding element
    // from array p and l
    List<int> q = new List<int>();
    for(int i = 0; i < A.Length; i++)
      q.Add((int) Math.Floor((double)p[i] / A[i]));
 
    // Check sum is divisible by
    // corresponding element or not
    List<int> z = new List<int>();
    for(int i = 0; i < q.Count; i++)
    {
 
      // First we divided element now multiple
      // to check perfect divisibility of element
      if (q[i] * A[i] == p[i])
        z.Add(A[i]);
    }
 
    // If no such element found return -1
    if (z.Count == 0)
      return new List<int>();
 
    return z;
  }
 
  // Driver code
  public static void Main(String []args)
  {
    int[] A = { 2, 4, 6, 8, 10, 12, 14 };
 
    // Calling function
    List<int> b = Factor(A);
 
    // Print required array
    foreach(int i in b)
      Console.Write(i+", ");
  }
}
 
 
// This code is contributed by 29AjayKumar

  <script>
      // JavaScript code for the above approach
 
      // Function to find element
      function Factor(A) {
 
          // Sum of all element
          let s = 0;
 
          for (let i = 0; i < A.length; i++) {
              s += A[i]
          }
 
          // Subtract each element from sum
          p = []
          for (i of A)
              p.push(s - i)
 
          // Divide corresponding element
          // from array p and l
          q = []
          for (i = 0; i < A.length; i++)
              q.push(Math.floor(p[i] / A[i]))
 
          // Check sum is divisible by
          // corresponding element or not
          z = []
          for (let i = 0; i < q.length; i++) {
 
              // First we divided element now multiple
              // to check perfect divisibility of element
              if (q[i] * A[i] == p[i])
                  z.push(A[i])
          }
          // If no such element found return -1
          if (z.length == 0)
              return -1
          return z
      }
      A = [2, 4, 6, 8, 10, 12, 14]
 
      // Calling function
      b = Factor(A)
 
      // Print required array
      document.write(b)
 
// This code is contributed by Potta Lokesh
  </script>

[2, 4, 8, 14]

Complejidad temporal: O(N)
Espacio auxiliar: O(N)

Enfoque eficiente: en este enfoque, no es necesario utilizar múltiples bucles y múltiples arrays. por lo que la complejidad del espacio y la complejidad del tiempo disminuirán. En esto, todas las operaciones de resta, división y multiplicación se realizan en un solo ciclo. Siga los pasos a continuación para resolver el problema:

• Inicialice la variable s como la suma de la array A[].
• Inicialice la array z[] para almacenar el resultado.
• Iterar sobre el rango [0, len(A)) usando las variables i y realizar las siguientes tareas:
  • Inicialice la variable a como sl[i], b como a/A[i].
  • Si b*A[i] es igual a a , agregue A[i] a z[].
• Después de realizar los pasos anteriores, imprima -1 si la array resultante está vacía; de lo contrario, imprima los elementos de la array z[] como respuesta.

A continuación se muestra la implementación del enfoque anterior.

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to find sum of all elements of an array
int sum(vector<int>& A)
{
  int res = 0;
  for (auto it : A)
    res += it;
  return res;
}
 
// Function to find element
vector<int> Factor(vector<int>& A)
{
 
  // Sum of all element
  int s = sum(A);
  vector<int> z;
 
  // Loop to find the factors of sum.
  for (int i = 0; i < A.size(); ++i) {
 
    // a is sum of remaining elements.
    int a = s - A[i];
 
    // b is integer value or factor of b.
    int b = a / A[i];
 
    // Check the divisibility
    if (b * A[i] == a)
      z.push_back(A[i]);
  }
 
  // If no element found return -1
  if (z.size() == 0)
    return { -1 };
 
  return z;
}
 
// Drive Code
 
int main()
{
  vector<int> A = { 2, 4, 6, 8, 10, 12, 14 };
 
  // Calling function
  vector<int> b = Factor(A);
 
  // Print resultant element
  for (auto it : b)
    cout << it << " ";
 
  return 0;
}
 
// This code is contributed by rakeshsahni

// Java program for the above approach
import java.util.*;
class GFG
{
 
  // Function to find sum of all elements of an array
  static int sum(int[] A)
  {
    int res = 0;
    for (int i = 0; i < A.length; i++) {
      res += A[i];
    }
    return res;
  }
 
  // Function to find element
  static ArrayList<Integer> Factor(int[] A)
  {
 
    // Sum of all element
    int s = sum(A);
    ArrayList<Integer> z = new ArrayList<Integer>();
 
    // Loop to find the factors of sum.
    for (int i = 0; i < A.length; ++i) {
 
      // a is sum of remaining elements.
      int a = s - A[i];
 
      // b is integer value or factor of b.
      int b = a / A[i];
 
      // Check the divisibility
      if (b * A[i] == a){
        z.add(A[i]);
      }
    }
 
    // If no element found return -1
    if (z.size() == 0){
      ArrayList<Integer> l1 = new ArrayList<Integer>();
      l1.add(-1);
      return l1;
    }
 
    return z;
  }
 
  // Drive Code
  public static void main (String[] args)
  {
    int A[] = new int[] { 2, 4, 6, 8, 10, 12, 14 };
 
    // Calling function
    ArrayList<Integer> b = Factor(A);
 
    // Print resultant element
    System.out.println(b);
  }
}
 
// This code is contributed by Shubham Singh

# Python program for the above approach
 
# Function to find element
def Factor(A):
 
    # Sum of all element
    s = sum(A)
    z = []
 
    # Loop to find the factors of sum.
    for i in range(len(A)):
 
        # a is sum of remaining elements.
        a = s-A[i]
 
        # b is integer value or factor of b.
        b = a//A[i]
 
        # Check the divisibility
        if b * A[i] == a:
            z.append(A[i])
 
    # If no element found return -1
    if len(z) == 0:
        return -1
 
    return z
 
 
A = [2, 4, 6, 8, 10, 12, 14]
 
# Calling function
b = Factor(A)
 
# Print resultant element
print(b)

// C# program for the above approach
using System;
using System.Collections.Generic;
class GFG {
 
  // Function to find sum of all elements of an array
  static int sum(List<int> A)
  {
    int res = 0;
    foreach(int it in A) res += it;
    return res;
  }
 
  // Function to find element
  static List<int> Factor(List<int> A)
  {
 
    // Sum of all element
    int s = sum(A);
    List<int> z = new List<int>();
 
    // Loop to find the factors of sum.
    for (int i = 0; i < A.Count; ++i) {
 
      // a is sum of remaining elements.
      int a = s - A[i];
 
      // b is integer value or factor of b.
      int b = a / A[i];
 
      // Check the divisibility
      if (b * A[i] == a)
        z.Add(A[i]);
    }
 
    // If no element found return -1
    if (z.Count == 0)
      return new List<int>() { -1 };
 
    return z;
  }
 
  // Drive Code
 
  public static void Main()
  {
    List<int> A
      = new List<int>() { 2, 4, 6, 8, 10, 12, 14 };
 
    // Calling function
    List<int> b = Factor(A);
 
    // Print resultant element
    Console.Write("[ ");
    int it;
    for (it = 0; it < b.Count - 1; it++) {
      Console.Write(b[it] + ", ");
    }
    Console.Write(b[it] + " ]");
  }
}
 
// This code is contributed by ukasp.

<script>
// JavaScript program for the above approach
 
// Function to find sum of all elements of an array
function sum(A)
{
  var res = 0;
  for (var it of A){
    res += parseInt(it);}
  return res;
}
 
// Function to find element
function Factor(A)
{
 
  // Sum of all element
  var s = sum(A);
   
  var z =[];
 
  // Loop to find the factors of sum.
  for (var i = 0; i < A.length; ++i) {
 
    // a is sum of remaining elements.
    var a = s - A[i];
 
    // b is integer value or factor of b.
    var b = parseInt(a / A[i]);
 
    // Check the divisibility
    if (b * A[i] == a)
      z.push(A[i]);
  }
 
  // If no element found return -1
  if (z.length == 0)
    return [ -1 ];
 
  return z;
}
 
// Drive Code
A = [ 2, 4, 6, 8, 10, 12, 14 ];
 
// Calling function
b = Factor(A);
 
// Print resultant element
for (var it of b)
document.write(it + " ");
 
//This code is contributed by Shubham Singh
</script>

[2, 4, 8, 14]

Complejidad temporal: O(N)
Espacio auxiliar: O(1)