Encuentre la relación de LCM a GCD de una array dada

Posted on by Rudeus Greyrat

Dada una array arr[] de enteros positivos, la tarea es encontrar la proporción de LCM y GCD de la array dada.
Ejemplos: 

Entrada: arr[] = {2, 3, 5, 9} 
Salida: 90:1 
Explicación: 
El GCD de la array dada es 1 y el LCM es 90. 
Por lo tanto, la relación se evalúa como 90:1.
Entrada: arr[] = {6, 12, 36} 
Salida: 6:1 
Explicación: 
El GCD de la array dada es 6 y el LCM es 36. 
Por lo tanto, la relación se evalúa como 6:1.  

Enfoque: 
siga los pasos a continuación para resolver los problemas: 
 

  1. En primer lugar, encontraremos el GCD de la array dada. Para este propósito, podemos usar la función incorporada para GCD proporcionada por STL o podemos usar el algoritmo euclidiano . 
     
  2. Luego, encontraremos el LCM de la array usando la siguiente fórmula: 
    LCM(a, b)=\frac{a*b}{gcd(a, b)}
     
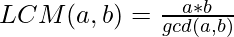
  3. Por último, encontraremos la proporción requerida.

A continuación se muestra la implementación del enfoque anterior: 

C++

// C++ Program to implement
// above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to calculate and
// return GCD of the given array
int findGCD(int arr[], int n)
{
    // Initialise GCD
    int gcd = arr[0];
    for (int i = 1; i < n; i++) {
        gcd = __gcd(arr[i], gcd);
 
        // Once GCD is 1, it
        // will always be 1 with
        // all other elements
        if (gcd == 1) {
            return 1;
        }
    }
 
    // Return GCD
    return gcd;
}
 
// Function to calculate and
// return LCM of the given array
int findLCM(int arr[], int n)
{
    // Initialise LCM
    int lcm = arr[0];
 
    // LCM of two numbers is
    // evaluated as [(a*b)/gcd(a, b)]
    for (int i = 1; i < n; i++) {
        lcm = (((arr[i] * lcm))
               / (__gcd(arr[i], lcm)));
    }
 
    // Return LCM
    return lcm;
}
 
// Function to print the ratio
// of LCM to GCD of the given array
void findRatio(int arr[], int n)
{
    int gcd = findGCD(arr, n);
    int lcm = findLCM(arr, n);
 
    cout << lcm / gcd << ":"
         << 1 << endl;
}
 
// Driver Code
int main()
{
    int arr[] = { 6, 12, 36 };
    int N = sizeof(arr) / sizeof(arr[0]);
 
    findRatio(arr, N);
 
    return 0;
}

Java

// Java Program to implement
// above approach
class GFG{
     
// Function to calculate and
// return GCD of the given array
static int __gcd(int a, int b)
{
    if (b == 0)
        return a;
    return __gcd(b, a % b);
}
 
static int findGCD(int arr[], int n)
{
    // Initialise GCD
    int gcd = arr[0];
    for (int i = 1; i < n; i++)
    {
        gcd = __gcd(arr[i], gcd);
 
        // Once GCD is 1, it
        // will always be 1 with
        // all other elements
        if (gcd == 1)
        {
            return 1;
        }
    }
 
    // Return GCD
    return gcd;
}
 
// Function to calculate and
// return LCM of the given array
static int findLCM(int arr[], int n)
{
    // Initialise LCM
    int lcm = arr[0];
 
    // LCM of two numbers is
    // evaluated as [(a*b)/gcd(a, b)]
    for (int i = 1; i < n; i++)
    {
        lcm = (((arr[i] * lcm)) /
          (__gcd(arr[i], lcm)));
    }
 
    // Return LCM
    return lcm;
}
 
// Function to print the ratio
// of LCM to GCD of the given array
static void findRatio(int arr[], int n)
{
    int gcd = findGCD(arr, n);
    int lcm = findLCM(arr, n);
 
    System.out.print((lcm / gcd));
    System.out.print(":1");
}
 
// Driver Code
public static void main (String[] args)
{
    int arr[] = new int[]{ 6, 12, 36 };
    int N = 3;
 
    findRatio(arr, N);
}
}
 
// This code is contributed by Ritik Bansal

Python3

# Python3 program to implement
# above approach
import math
 
# Function to calculate and
# return GCD of the given array
def findGCD(arr, n):
     
    # Initialise GCD
    gcd = arr[0]
 
    for i in range(1, n):
        gcd = int(math.gcd(arr[i], gcd))
         
        # Once GCD is 1, it
        # will always be 1 with
        # all other elements
        if (gcd == 1):
            return 1
             
    # Return GCD
    return gcd
 
# Function to calculate and
# return LCM of the given array
def findLCM(arr, n):
     
    # Initialise LCM
    lcm = arr[0]
 
    # LCM of two numbers is
    # evaluated as [(a*b)/gcd(a, b)]
    for i in range(1, n):
        lcm = int((((arr[i] * lcm)) /
           (math.gcd(arr[i], lcm))))
 
    # Return LCM
    return lcm
 
# Function to print the ratio
# of LCM to GCD of the given array
def findRatio(arr, n):
     
    gcd = findGCD(arr, n)
    lcm = findLCM(arr, n)
     
    print(int(lcm / gcd), ":", "1")
 
# Driver Code
arr = [ 6, 12, 36 ]
N = len(arr)
 
findRatio(arr, N)
 
# This code is contributed by sanjoy_62

C#

// C# Program to implement
// above approach
using System;
class GFG{
     
// Function to calculate and
// return GCD of the given array
static int __gcd(int a, int b)
{
    if (b == 0)
        return a;
    return __gcd(b, a % b);
}
 
static int findGCD(int []arr, int n)
{
    // Initialise GCD
    int gcd = arr[0];
    for (int i = 1; i < n; i++)
    {
        gcd = __gcd(arr[i], gcd);
 
        // Once GCD is 1, it
        // will always be 1 with
        // all other elements
        if (gcd == 1)
        {
            return 1;
        }
    }
 
    // Return GCD
    return gcd;
}
 
// Function to calculate and
// return LCM of the given array
static int findLCM(int []arr, int n)
{
    // Initialise LCM
    int lcm = arr[0];
 
    // LCM of two numbers is
    // evaluated as [(a*b)/gcd(a, b)]
    for (int i = 1; i < n; i++)
    {
        lcm = (((arr[i] * lcm)) /
          (__gcd(arr[i], lcm)));
    }
 
    // Return LCM
    return lcm;
}
 
// Function to print the ratio
// of LCM to GCD of the given array
static void findRatio(int []arr, int n)
{
    int gcd = findGCD(arr, n);
    int lcm = findLCM(arr, n);
 
    Console.Write((lcm / gcd));
    Console.Write(":1");
}
 
// Driver Code
public static void Main()
{
    int []arr = new int[]{ 6, 12, 36 };
    int N = 3;
 
    findRatio(arr, N);
}
}
 
// This code is contributed by Code_Mech

Javascript

<script>
// javascript Program to implement
// above approach   
 
    // Function to calculate and
    // return GCD of the given array
    function __gcd(a , b)
    {
        if (b == 0)
            return a;
        return __gcd(b, a % b);
    }
 
    function findGCD(arr, n)
    {
     
        // Initialise GCD
        var gcd = arr[0];
        for (i = 1; i < n; i++)
        {
            gcd = __gcd(arr[i], gcd);
 
            // Once GCD is 1, it
            // will always be 1 with
            // all other elements
            if (gcd == 1) {
                return 1;
            }
        }
 
        // Return GCD
        return gcd;
    }
 
    // Function to calculate and
    // return LCM of the given array
    function findLCM(arr, n)
    {
     
        // Initialise LCM
        var lcm = arr[0];
 
        // LCM of two numbers is
        // evaluated as [(a*b)/gcd(a, b)]
        for (i = 1; i < n; i++)
        {
            lcm = (((arr[i] * lcm)) / (__gcd(arr[i], lcm)));
        }
 
        // Return LCM
        return lcm;
    }
 
    // Function to print the ratio
    // of LCM to GCD of the given array
    function findRatio(arr , n) {
        var gcd = findGCD(arr, n);
        var lcm = findLCM(arr, n);
 
        document.write((lcm / gcd));
        document.write(":1");
    }
 
    // Driver Code
        var arr = [ 6, 12, 36 ];
        var N = 3;
 
        findRatio(arr, N);
 
// This code is contributed by todaysgaurav.
</script>
Producción: 

6:1

 

Complejidad de tiempo: O(N * logN) 
Espacio auxiliar: O(1)
 

Publicación traducida automáticamente

Artículo escrito por shauryarehangfg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *