La trigonometría es la relación entre los ángulos y los lados de un triángulo rectángulo. En un triángulo rectángulo, hay 3 ángulos de los cuales un ángulo es un ángulo recto (90°) y otros dos ángulos son ángulos agudos y hay 3 lados. El lado opuesto al ángulo recto se llama hipotenusa. Hay 6 razones entre estos lados basadas en el ángulo entre ellos y se llaman razones trigonométricas.
Las 6 razones trigonométricas son:
- Seno (pecado)
- Coseno (cos)
- Tangente (bronceado)
- Cosecante (cosec)
- secante (seg)
- Cotangente (cuna)
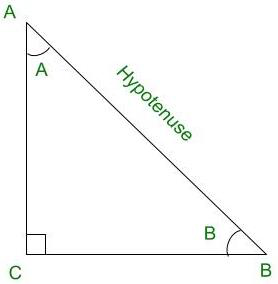
Triángulo rectángulo ACB
Seno (pecado):
El seno de un ángulo se define por la relación entre las longitudes de los lados opuestos al ángulo y la hipotenusa. Para el triángulo anterior, sen A = BC/AB
Coseno (cos):
El coseno de un ángulo se define por la relación entre las longitudes de los lados adyacentes al ángulo y la hipotenusa. Para el triángulo anterior, cos A = AC/AB
Tangente (bronceado):
La tangente de un ángulo se define por la relación entre la longitud de los lados opuestos al ángulo y el lado adyacente al ángulo. Para el triángulo anterior, tan A = BC/AC
Cosecante (cosec):
La cosecante de un ángulo se define por la relación entre la longitud de la hipotenusa y el lado opuesto al ángulo. Para el triángulo anterior, cosec A = AB/BC
Secante (s):
La secante de un ángulo se define por la relación entre la longitud de la hipotenusa y el lado y el lado adyacente al ángulo Para el triángulo anterior, sec A = AB/AC
Cotangente (cot):
La cotangente de un ángulo se define por la relación entre la longitud de los lados adyacentes al ángulo y el lado opuesto al ángulo. Para el triángulo anterior, cot A = AC/BC
Encuentra sen2x, cos2x y tan2x a partir de la información dada. csc (x) = 6, tan (x) < 0.
Solución:

Triángulo rectángulo XYZ
Se da que, cosecX = 6
Sabemos que, senX = 1/cosecX
⇒ senX = 1/6 ………………..( 1 )
⇒ senX es positivo
Se da que, tanX < 0
⇒ tanX es negativo
Como senX es positivo y tanX es negativo
⇒ X se encuentra en el 2do Cuadrante.
Sabemos que, cos 2 X = 1 – sen 2 X
⇒ porque 2 X = 1 – (1/6) 2
⇒ porque 2 X = 35 / 36
⇒ cos X = ± √35 / 6
Pero, dado que X se encuentra en el segundo cuadrante y la cosecante es negativa en el segundo cuadrante,
⇒ cosX = – √35 / 6 ……………….(2)
sin(2X) = 2.sinX.cosX
De (1) y (2),
⇒ sin(2X) = 2.(1/6).(– √35 / 6)
⇒ sin(2X) = – √35/18 …………………(3)
cos(2X) = cos 2 X – sen 2 X
De (1) y (2),
⇒ cos(2X) = ( – √35 / 6) 2 – (1 / 6) 2
⇒ cos(2X) = 35 / 36 – 1 / 36
⇒ cos(2X) = 34 / 36
⇒ cos(2X) = 17 / 18 …………………( 4 )
tan(2X) = sen(2X) / cos(2X)
De (3) y (4),
⇒ tan(2X) = (– √35 / 18) / (17 / 18)
⇒ tan(2X) = – √35 / 17
Por lo tanto, los valores de sen(2X), cos(2X) y tan(2X) son – √35 / 18, 17 / 18 y – √35 / 17 respectivamente.
Preguntas similares
Pregunta 1: Encuentra sen(2X),cos(2X) y tan(2X) a partir de la información dada: secX = 8, X se encuentra en el Cuadrante IV
Solución:
Se da que, secX = 8
Sabemos que, cosX = 1 / segX
⇒ cosX = 1 / 8 ………………..( 1 )
Sabemos que, sen 2 X = 1 – cos 2 X
⇒ sen 2 X = 1 – ( 1 / 8 ) 2
⇒ sen 2 X = 1 – 1/64
⇒ sen 2 X = 63 / 64
⇒ senX = ± √63 / √64
⇒ senX = ± 3√7 / 8
Como Seno( sin ) es negativo en el Cuadrante IV,
⇒ senX = – 3√7 / 8 ……………….( 2 )
sin( 2X ) = 2.sinX.cosX
De (1) y (2),
⇒ sen( 2X ) = 2.( – 3√7 / 8).(1 / 8)
⇒ sen( 2X ) = – 3√7 / 32 ………………..( 3 )
cos( 2X ) = cos 2X – sen 2X
De (1) y (2),
⇒ cos( 2X ) = (1 / 8) 2 – (– 3√7 / 8) 2
⇒ cos( 2X ) = (1 / 64) – (63 / 64)
⇒ cos( 2X ) = – 62 / 64
⇒ cos( 2X ) = – 31 / 32 ………………..( 4 )
tan( 2X ) = sen( 2X ) / cos( 2X )
De (3) y (4),
⇒ tan( 2X ) = (– 3√7 / 32) / ( – 31 / 32)
⇒ tan( 2X ) = 3√7 / 31
Por lo tanto, los valores de sin( 2X ), cos( 2X ) y tan( 2X ) son – 3√7 / 32, – 31 / 32 y 3√7 / 31 respectivamente.
Pregunta 2: Encuentra sen(2X), cos(2X) y tan(2X) a partir de la información dada: senX = 3/5, X se encuentra en el Cuadrante I
Solución:
Se da que, senX = 3/5 ……………….( 1 )
Sabemos que, cos 2 X = 1 – sen 2 X
⇒ porque 2 X = 1 – ( 3 / 5 ) 2
⇒ porque 2 X = 16 / 25
⇒ cos X = ± 4 / 5
Dado que X se encuentra en el 1er cuadrante y la cosecante es positiva en el 1er cuadrante,
⇒ cosX = 4 / 5 ……………….( 2 )
sin( 2X ) = 2.sinX.cosX
De (1) y (2),
⇒ sen( 2X ) = 2.( 3/5 ).( 4/5)
⇒ sen( 2X ) = 24 / 25 ………………..( 3 )
cos( 2X ) = cos 2X – sen 2X
De (1) y (2),
⇒ cos( 2X ) = ( 4/5 ) 2 – ( 3/5 ) 2
⇒ cos( 2X ) = 16/25 – 9/25
⇒ cos( 2X ) = 7/25 …………………..( 4 )
tan( 2X ) = sen( 2X ) / cos(2X)
De (3) y (4),
⇒ tan( 2X ) = ( 24/25 ) / (7/25)
⇒ tan( 2X ) = 24/7
Por lo tanto, los valores de sin(2X), cos(2X) y tan(2X) son 24/25, 7/25 y 24/7 respectivamente.
Pregunta 3: Encuentra sen(2X),cos(2X) y tan(2X) a partir de la información dada: cosX = 15/17, X se encuentra en el Cuadrante IV
Solución:
Se da que, cosX = 15/17 ……………….(1)
Sabemos que, sen 2 X = 1 – cos 2 X
⇒ sen 2 X = 1 – ( 15/17 ) 2
⇒ sen 2 X = 1 – 225 / 289
⇒ sen 2 X = 64 / 289
⇒ senX = ± 8 / 17
Dado que X se encuentra en el 1.er cuadrante y Sine( sin ) es positivo en el 4.º cuadrante,
⇒ senX = – 8/17 ……………….(2)
sin( 2X ) = 2.sinX.cosX
De (1) y (2),
⇒ sen( 2X ) = 2.( – 8/17 ).(15/17)
⇒ sin(2X) = – 240/289 ………………..( 3 )
cos(2X) = cos 2 X – sen 2 X
De (1) y (2),
⇒ cos(2X) = (15/17) 2 – (– 8/17) 2
⇒ cos(2X) = 225/289 – 64/289
⇒ cos(2X) = 161/289 …………………..( 4 )
tan(2X) = sen(2X) / cos(2X)
De (3) y (4),
⇒ tan(2X) = (– 240/289) / (161/289)
⇒ tan(2X) = – 240/289
Por lo tanto, los valores de sin(2X), cos(2X) y tan(2X) son – 240/289, 161/289 y – 240/289 respectivamente.
Publicación traducida automáticamente
Artículo escrito por rajsanghavi9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA