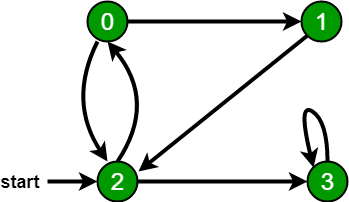
Dado un gráfico dirigido y dos vértices en él, compruebe si hay un camino desde el primer vértice dado hasta el segundo.
Ejemplo:
Considere el siguiente gráfico:
Entrada: (u, v) = (1, 3)
Salida: Sí
Explicación:
Hay un camino de 1 a 3, 1 -> 2 -> 3Entrada: (u, v) = (3, 6)
Salida: No
Explicación:
No hay ruta de 3 a 6
Aquí se analiza una solución basada en BFS o DFS para este problema .
Enfoque: aquí discutiremos una solución basada en programación dinámica utilizando el algoritmo Floyd Warshall .
- Cree un tapete de array 2D booleano donde mat [i][j] será verdadero si hay una ruta desde el vértice i hasta j .
- Para cada vértice inicial i y el vértice final j itere sobre todos los vértices intermedios k y verifique si hay un camino para i a j a través de k y luego marque mat[i][j] como verdadero.
- Finalmente, verifique si mat[u][v] es verdadero y luego devuelva verdadero; de lo contrario, devuelva falso.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to find if there is a
// path between two vertices in a
// directed graph using Dynamic Programming
#include <bits/stdc++.h>
using namespace std;
#define X 6
#define Z 2
// function to find if there is a
// path between two vertices in a
// directed graph
bool existPath(int V, int edges[X][Z],
int u, int v)
{
// dp matrix
bool mat[V][V];
memset(mat, false, sizeof(mat));
// set dp[i][j]=true if there is
// edge between i to j
for (int i = 0; i < X; i++)
mat[edges[i][0]][edges[i][1]] = true;
// check for all intermediate vertex
for (int k = 0; k < V; k++) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
mat[i][j] = mat[i][j]
|| mat[i][k]
&& mat[k][j];
}
}
}
// if vertex is invalid
if (u >= V || v >= V) {
return false;
}
// if there is a path
if (mat[u][v])
return true;
return false;
}
// Driver function
int main()
{
int V = 4;
int edges[X][Z]
= { { 0, 2 }, { 0, 1 },
{ 1, 2 }, { 2, 3 },
{ 2, 0 }, { 3, 3 } };
int u = 1, v = 3;
if (existPath(V, edges, u, v))
cout << "Yes\n";
else
cout << "No\n";
return 0;
}
Java
// Java program to find if there is a path
// between two vertices in a directed graph
// using Dynamic Programming
import java.util.*;
class GFG{
static final int X = 6;
static final int Z = 2;
// Function to find if there is a
// path between two vertices in a
// directed graph
static boolean existPath(int V, int edges[][],
int u, int v)
{
// mat matrix
boolean [][]mat = new boolean[V][V];
// set mat[i][j]=true if there is
// edge between i to j
for (int i = 0; i < X; i++)
mat[edges[i][0]][edges[i][1]] = true;
// Check for all intermediate vertex
for(int k = 0; k < V; k++)
{
for(int i = 0; i < V; i++)
{
for(int j = 0; j < V; j++)
{
mat[i][j] = mat[i][j] ||
mat[i][k] &&
mat[k][j];
}
}
}
// If vertex is invalid
if (u >= V || v >= V)
{
return false;
}
// If there is a path
if (mat[u][v])
return true;
return false;
}
// Driver code
public static void main(String[] args)
{
int V = 4;
int edges[][] = { { 0, 2 }, { 0, 1 },
{ 1, 2 }, { 2, 3 },
{ 2, 0 }, { 3, 3 } };
int u = 1, v = 3;
if (existPath(V, edges, u, v))
System.out.print("Yes\n");
else
System.out.print("No\n");
}
}
// This code is contributed by Princi Singh
Python3
# Python3 program to find if there
# is a path between two vertices in a
# directed graph using Dynamic Programming
X = 6
Z = 2
# Function to find if there is a
# path between two vertices in a
# directed graph
def existPath(V, edges, u, v):
# dp matrix
mat = [[False for i in range(V)]
for j in range(V)]
# Set dp[i][j]=true if there is
# edge between i to j
for i in range(X):
mat[edges[i][0]][edges[i][1]] = True
# Check for all intermediate vertex
for k in range(V):
for i in range(V):
for j in range(V):
mat[i][j] = (mat[i][j] or
mat[i][k] and
mat[k][j])
# If vertex is invalid
if (u >= V or v >= V):
return False
# If there is a path
if (mat[u][v]):
return True
return False
# Driver code
V = 4
edges = [ [ 0, 2 ], [ 0, 1 ],
[ 1, 2 ], [ 2, 3 ],
[ 2, 0 ], [ 3, 3 ] ]
u, v = 1, 3
if (existPath(V, edges, u, v)):
print("Yes")
else:
print("No")
# This code is contributed by divyeshrabadiya07
C#
// C# program to find if there is a path
// between two vertices in a directed graph
// using Dynamic Programming
using System;
class GFG{
static readonly int X = 6;
static readonly int Z = 2;
// Function to find if there is a
// path between two vertices in a
// directed graph
static bool existPath(int V, int [,]edges,
int u, int v)
{
// mat matrix
bool [,]mat = new bool[V, V];
// set mat[i,j]=true if there is
// edge between i to j
for (int i = 0; i < X; i++)
mat[edges[i, 0], edges[i, 1]] = true;
// Check for all intermediate vertex
for(int k = 0; k < V; k++)
{
for(int i = 0; i < V; i++)
{
for(int j = 0; j < V; j++)
{
mat[i, j] = mat[i, j] ||
mat[i, k] &&
mat[k, j];
}
}
}
// If vertex is invalid
if (u >= V || v >= V)
{
return false;
}
// If there is a path
if (mat[u, v])
return true;
return false;
}
// Driver code
public static void Main(String[] args)
{
int V = 4;
int [,]edges = { { 0, 2 }, { 0, 1 },
{ 1, 2 }, { 2, 3 },
{ 2, 0 }, { 3, 3 } };
int u = 1, v = 3;
if (existPath(V, edges, u, v))
Console.Write("Yes\n");
else
Console.Write("No\n");
}
}
// This code is contributed by sapnasingh4991
Javascript
<script>
// Javascript program to find if there is a path
// between two vertices in a directed graph
// using Dynamic Programming
var X = 6;
var Z = 2;
// Function to find if there is a
// path between two vertices in a
// directed graph
function existPath(V, edges, u, v)
{
// mat matrix
var mat = Array.from(Array(V), ()=>Array(V));
// set mat[i,j]=true if there is
// edge between i to j
for (var i = 0; i < X; i++)
mat[edges[i][0]][edges[i][1]] = true;
// Check for all intermediate vertex
for(var k = 0; k < V; k++)
{
for(var i = 0; i < V; i++)
{
for(var j = 0; j < V; j++)
{
mat[i][j] = mat[i][j] ||
mat[i][k] &&
mat[k][j];
}
}
}
// If vertex is invalid
if (u >= V || v >= V)
{
return false;
}
// If there is a path
if (mat[u][v])
return true;
return false;
}
// Driver code
var V = 4;
var edges = [ [ 0, 2 ], [ 0, 1 ],
[ 1, 2 ], [ 2, 3 ],
[ 2, 0 ], [ 3, 3 ] ];
var u = 1, v = 3;
if (existPath(V, edges, u, v))
document.write("Yes<br>");
else
document.write("No<br>");
</script>
Yes
Tiempo Complejidad : O ( V 3 )
Espacio Auxiliar : O ( V 2 )
Publicación traducida automáticamente
Artículo escrito por animesh_ghosh y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA