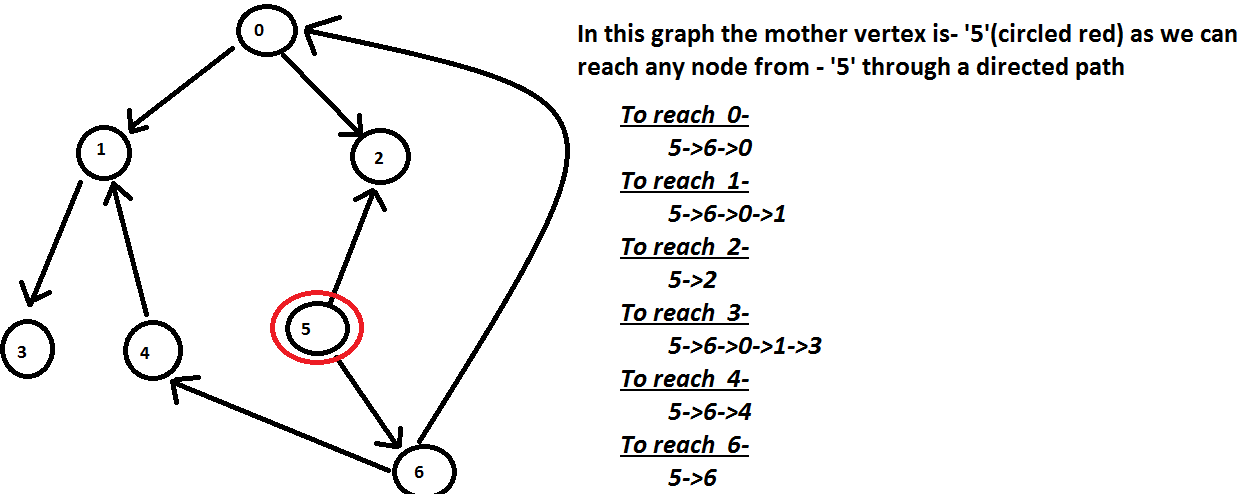
Un vértice madre en un gráfico G = (V, E) es un vértice v tal que un camino desde v puede llegar a todos los demás vértices en G por un camino desde v.
Ejemplo:
Aporte:
Salida:
5
Enfoque:
podemos resolver este problema utilizando el enfoque de búsqueda en profundidad primero . Para optimizar aún más nuestro enfoque, utilizaremos una solución eficiente.
La siguiente solución también utiliza la búsqueda en profundidad primero para resolver este problema, pero ejecuta el ciclo de búsqueda en profundidad primero solo una vez, y tan pronto como encuentra el vértice madre, detiene la ejecución.
- Al ejecutar la primera búsqueda en profundidad, tenemos una array de máscara de bits que representa una máscara de bits para cada vértice. Esta array de máscara de bits se pasa a todos los vértices durante la ejecución.
- Cada vértice modifica su máscara de bits dedicada de tal manera que todos los bits establecidos que representan los vértices se pueden visitar desde este vértice, incluido el vértice actual.
- En cada iteración, verificamos si todos los vértices se pueden visitar desde este vértice al verificar el valor actual de la máscara de bits del vértice (si los bits que representan a todos los vértices están configurados). Si se pueden visitar todos los vértices desde este vértice, interrumpe la ejecución y encuentra el vértice madre como el vértice actual.
- Si el vértice-2 ha sido visitado desde el vértice-1, y el vértice-2 ya ha sido visitado anteriormente, entonces el vértice-1 actualiza su máscara de bits haciendo una operación OR con la máscara de bits del vértice-2.
Complejidad del tiempo: O(V+E)
¿Cómo funciona la idea anterior?
Deje que este enfoque admita un gráfico que tenga un máximo de 32 vértices. Este método también se puede aumentar para admitir más vértices, pero aquí se trata con un máximo de 32 vértices.
- Se crea una array de máscara de bits de máscaras de 32 bits. El índice 0 de la array denota la máscara de bits para el vértice-0, mientras que el primer índice de la array denota la máscara de bits para el vértice-1, y así sucesivamente.
- Todos los vértices del gráfico se visitan mediante el algoritmo de búsqueda en profundidad primero y se pasa la misma array de máscara de bits a todos los vértices. Los valores de máscara de bits se establecen en consecuencia para representar todos los vértices que se pueden visitar desde este vértice.
- El índice de bits se establece en correspondencia con los vértices vecinos, incluido el índice de bits propio. Los vértices vecinos también repetirán lo mismo para su máscara de bits y devolverán lo mismo a Vertex-1.
- Vertex-1 seguirá realizando la operación OR en el valor de retorno de todos los vecinos a su máscara de bits para representar todos los vértices que se pueden visitar desde el vértice-1.
- Tenga en cuenta que si el vértice-2 es vecino del vértice-1 y ya ha sido visitado desde otro vértice vecino, no volverá a visitar el vértice de su vecino y devolverá su máscara de bits al primer Node.
- Cada iteración verificará si la máscara de bits correspondiente al vértice actual tiene todos los bits establecidos en 1. Si todos los bits están establecidos en 1 para el vértice actual significa que todos los vértices se pueden visitar desde el vértice actual, y el vértice actual es el vértice madre de la gráfica.
A continuación se muestra la implementación de nuestro enfoque anterior:
C++
#include<bits/stdc++.h>
using namespace std;
void PrintGraph(vector<vector<int>> adj)
{
int n=(int)adj.size();
for(int i=0;i<n;i++)
{
for(auto x:adj[i])
{
cout << "There is an edge from " << i <<" to " << x << '\n';
}
}
}
bool IsEdge(vector<vector<int>> adj,int src, int dest)
{
for(auto x:adj[src])
{
if(x==dest)
return true;
}
return false;
}
int MotherVertexUtil(
vector<vector<int>> adj, int index,
vector<int> mask, int* m_vertex)
{
int n=(int)adj.size();
// If mother vertex is already found
// then simply return with existing
// mask of the vertex index
if (*m_vertex != -1) {
return mask[index];
}
// if this vertex is already visited,
// return the bit-mask
// value of this vertex.
if (mask[index] != 0) {
return mask[index];
}
int tmpmask = 0;
// Set the bit corresponding
// to vertex index in tmpmask
tmpmask |= (1 << index);
for (int i = 0; i < n; i++) {
if ((index != i)
&& IsEdge(adj, index, i)) {
// Set bits corresponding to all
// vertex which can be visited
// by this vertex by ORing
// the return value by util function
// Vertex is not visited
if (mask[i] == 0) {
int retmask
= MotherVertexUtil(
adj, i, mask, m_vertex);
tmpmask |= retmask;
}
// Vertex is already visited
else {
tmpmask |= mask[i];
}
// Check if current vertex is
// mother vertex or mother vertex
// is already found
if (tmpmask == (pow(2, n) - 1)) {
// If all bits of a mask is set
// it means current vertex
// is mother vertex
if (*m_vertex == -1) {
*m_vertex = index;
}
return tmpmask;
}
}
}
// populate tmpmask as final
// bit mask of the vertex
mask[index] |= tmpmask;
return mask[index];
}
int MotherVertex(vector<vector<int>> adj)
{
int n=adj.size();
vector<int> mask(n);
// Initially bit mask
// for all vertex will be 0
for(int i=0;i<n;i++)
mask[i]=0;
// DFS traversal is used to check
// for the mother vertex
// All set bits (of bitmask of a vertex)
// represent the current vertex index
// and index of vertices which could be
// visited from the current vertex.
/* Example:
If a vertex index is 3
then and vertex 5, 7 and 10
can be visited from this vertex
then final bit mask of this vertex
would be
00000000000000000000010010101000
(bits 3, 5, 7 and 10 are set) */
// tmpmask is used to store
// the final bitmask of the vertex.
int tmpmask = 0;
// flag to check if
// mother vertex is found
int m_vertex = -1;
for (int index = 0; index < n; index++) {
// set the bit corresponding
// to vertex index in tmpmask
tmpmask = (1 << index);
// mask for a vertex is 0
// means it has not yet
// visited so visit this vertex
if (mask[index] == 0) {
int retmask= MotherVertexUtil(adj, index,mask, &m_vertex);
// set bits corresponding to all
// vertices which can be visited
// from this vertex by ORing
// the return value by util function
tmpmask |= retmask;
}
// check if current vertex is
// mother vertex or mother vertex
// is already found
// If all bits of a mask is set
// it means current vertex
// is mother vertex
if (tmpmask == (pow(2, n) - 1)) {
// current vertex is mother vertex
if (m_vertex == -1) {
m_vertex = index;
}
break;
}
// populate tmpmask as final bit
// mask of the vertex
mask[index] |= tmpmask;
}
return m_vertex;
}
int main()
{
int n;
n = 7;
vector<vector<int>> adj(n);
adj[0].push_back(2);
adj[0].push_back(1);
adj[1].push_back(3);
adj[4].push_back(1);
adj[5].push_back(2);
adj[5].push_back(6);
adj[6].push_back(0);
adj[6].push_back(4);
PrintGraph(adj);
int m_vertex = MotherVertex(adj);
if( m_vertex == -1)
{
cout << "Mother vertex is not existing in this graph\n";
}
else
{
cout << "Mother vertex is: " << m_vertex << '\n';
}
return 0;
}
Java
// Java code for above implementation
import java.util.*;
public class Main {
public static void main(String[] args)
{
int n = 7;
ArrayList<ArrayList<Integer> > adj
= new ArrayList<>();
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
}
adj.get(0).add(2);
adj.get(0).add(1);
adj.get(1).add(3);
adj.get(4).add(1);
adj.get(5).add(2);
adj.get(5).add(6);
adj.get(6).add(0);
adj.get(6).add(4);
PrintGraph(adj);
int m_vertex = MotherVertex(adj);
if (m_vertex == -1) {
System.out.println(
"Mother vertex is not existing in this graph");
}
else {
System.out.println("Mother vertex is: "
+ m_vertex);
}
}
public static void
PrintGraph(ArrayList<ArrayList<Integer> > adj)
{
int n = adj.size();
for (int i = 0; i < n; i++) {
for (int x : adj.get(i)) {
System.out.println("There is an edge from "
+ i + " to " + x);
}
}
}
public static boolean
IsEdge(ArrayList<ArrayList<Integer> > adj, int src,
int dest)
{
for (int x : adj.get(src)) {
if (x == dest)
return true;
}
return false;
}
public static int
MotherVertexUtil(ArrayList<ArrayList<Integer> > adj,
int index, int[] mask, int m_vertex)
{
int n = adj.size();
// If mother vertex is already found
// then simply return with existing
// mask of the vertex index
if (m_vertex != -1) {
return mask[index];
}
// if this vertex is already visited,
// return the bit-mask
// value of this vertex.
if (mask[index] != 0) {
return mask[index];
}
int tmpmask = 0;
// Set the bit corresponding
// to vertex index in tmpmask
tmpmask |= (1 << index);
for (int i = 0; i < n; i++) {
if ((index != i) && IsEdge(adj, index, i)) {
// Set bits corresponding to all
// vertex which can be visited
// by this vertex by ORing
// the return value by util function
// Vertex is not visited
if (mask[i] == 0) {
int retmask = MotherVertexUtil(
adj, i, mask, m_vertex);
tmpmask |= retmask;
}
// Vertex is already visited
else {
tmpmask |= mask[i];
}
// Check if current vertex is
// mother vertex or mother vertex
// is already found
if (tmpmask == (Math.pow(2, n) - 1)) {
// If all bits of a mask is set
// it means current vertex
// is mother vertex
if (m_vertex == -1) {
m_vertex = index;
}
return tmpmask;
}
}
}
// populate tmpmask as final
// bit mask of the vertex
mask[index] |= tmpmask;
return mask[index];
}
public static int
MotherVertex(ArrayList<ArrayList<Integer> > adj)
{
int n = adj.size();
int[] mask = new int[n];
// Initially bit mask
// for all vertex will be 0
for (int i = 0; i < n; i++)
mask[i] = 0;
// DFS traversal is used to check
// for the mother vertex
// All set bits (of bitmask of a vertex)
// represent the current vertex index
// and index of vertices which could be
// visited from the current vertex.
/* Example:
If a vertex index is 3
then and vertex 5, 7 and 10
can be visited from this vertex
then final bit mask of this vertex
would be
00000000000000000000010010101000
(bits 3, 5, 7 and 10 are set) */
// tmpmask is used to store
// the final bitmask of the vertex.
int tmpmask = 0;
// flag to check if
// mother vertex is found
int m_vertex = -1;
for (int index = 0; index < n; index++) {
// set the bit corresponding
// to vertex index in tmpmask
tmpmask = (1 << index);
// mask for a vertex is 0
// means it has not yet
// visited so visit this vertex
if (mask[index] == 0) {
int retmask = MotherVertexUtil(
adj, index, mask, m_vertex);
// set bits corresponding to all
// vertices which can be visited
// from this vertex by ORing
// the return value by util function
tmpmask |= retmask;
}
// check if current vertex is
// mother vertex or mother vertex
// is already found
// If all bits of a mask is set
// it means current vertex
// is mother vertex
if (tmpmask == (Math.pow(2, n) - 1)) {
// current vertex is mother vertex
if (m_vertex == -1) {
m_vertex = index;
}
break;
}
// populate tmpmask as final bit
// mask of the vertex
mask[index] |= tmpmask;
}
return m_vertex;
}
}
// This code is contributed by Tapesh (tapeshdua420)
Python3
def PrintGraph(adj):
n = len(adj)
for i in range(n):
for x in adj[i]:
print("There is an edge from {} to {}".format(i, x))
def IsEdge(adj, src, dest):
for x in adj[src]:
if(x == dest):
return True
return False
def MotherVertexUtil(adj, index, mask, m_vertex):
n = len(adj)
# If mother vertex is already found
# then simply return with existing
# mask of the vertex index
if (m_vertex[0] != -1):
return mask[index]
# if this vertex is already visited,
# return the bit-mask
# value of this vertex.
if (mask[index] != 0):
return mask[index]
tmpmask = 0
# Set the bit corresponding
# to vertex index in tmpmask
tmpmask |= (1 << index)
for i in range(n):
if ((index != i) and IsEdge(adj, index, i)):
# Set bits corresponding to all
# vertex which can be visite
# by this vertex by ORing
# the return value by util function
# Vertex is not visited
if (mask[i] == 0):
retmask = MotherVertexUtil(adj, i, mask, m_vertex)
tmpmask |= retmask
# Vertex is already visited
else:
tmpmask |= mask[i]
# Check if current vertex is
# mother vertex or mother vertex
# is already found
if (tmpmask == (pow(2, n) - 1)):
# If all bits of a mask is set
# it means current vertex
# is mother vertex
if (m_vertex[0] == -1):
m_vertex[0] = index
return tmpmask
# populate tmpmask as final
# bit mask of the vertex
mask[index] |= tmpmask
return mask[index]
def MotherVertex(adj):
n = len(adj)
mask = [0]*n
# Initially bit mask
# for all vertex will be 0
for i in range(n):
mask[i] = 0
# DFS traversal is used to check
# for the mother vertex
# All set bits (of bitmask of a vertex)
# represent the current vertex index
# and index of vertices which could be
# visited from the current vertex.
# Example:
# If a vertex index is 3
# then and vertex 5, 7 and 10
# can be visited from this vertex
# then final bit mask of this vertex
# would be
# 00000000000000000000010010101000
# (bits 3, 5, 7 and 10 are set)
# tmpmask is used to store
# the final bitmask of the vertex.
tmpmask = 0
# flag to check if
# mother vertex is found
m_vertex = [-1, ]
for index in range(n):
# set the bit corresponding
# to vertex index in tmpmask
tmpmask = (1 << index)
# mask for a vertex is 0
# means it has not yet
# visited so visit this vertex
if (mask[index] == 0):
retmask = MotherVertexUtil(adj, index, mask, m_vertex)
# set bits corresponding to all
# vertices which can be visited
# from this vertex by ORing
# the return value by util function
tmpmask |= retmask
# check if current vertex is
# mother vertex or mother vertex
# is already found
# If all bits of a mask is set
# it means current vertex
# is mother vertex
if (tmpmask == (pow(2, n) - 1)):
# current vertex is mother vertex
if (m_vertex[0] == -1):
m_vertex[0] = index
break
# populate tmpmask as final bit
# mask of the vertex
mask[index] |= tmpmask
return m_vertex[0]
if __name__ == '__main__':
n = 7
adj = [[] for _ in range(n)]
adj[0].append(2)
adj[0].append(1)
adj[1].append(3)
adj[4].append(1)
adj[5].append(2)
adj[5].append(6)
adj[6].append(0)
adj[6].append(4)
PrintGraph(adj)
m_vertex = MotherVertex(adj)
if(m_vertex == -1):
print("Mother vertex is not existing in this graph")
else:
print("Mother vertex is:", m_vertex)
C#
// C# code for above implementation
using System;
using System.Collections.Generic;
using System.Linq;
class Program {
public static void Main(string[] args)
{
int n = 7;
List<List<int> > adj = new List<List<int> >();
for (int i = 0; i < n; i++) {
adj.Add(new List<int>());
}
adj[0].Add(2);
adj[0].Add(1);
adj[1].Add(3);
adj[4].Add(1);
adj[5].Add(2);
adj[5].Add(6);
adj[6].Add(0);
adj[6].Add(4);
PrintGraph(adj);
int m_vertex = MotherVertex(adj);
if (m_vertex == -1) {
Console.WriteLine(
"Mother vertex is not existing in this graph");
}
else {
Console.WriteLine("Mother vertex is: "
+ m_vertex);
}
}
public static void PrintGraph(List<List<int> > adj)
{
int n = adj.Count();
for (int i = 0; i < n; i++) {
foreach(var x in adj[i])
{
Console.WriteLine("There is an edge from "
+ i + " to " + x);
}
}
}
public static bool IsEdge(List<List<int> > adj, int src,
int dest)
{
foreach(var x in adj[src])
{
if (x == dest)
return true;
}
return false;
}
public static int MotherVertexUtil(List<List<int> > adj,
int index,
int[] mask,
int m_vertex)
{
int n = adj.Count();
// If mother vertex is already found
// then simply return with existing
// mask of the vertex index
if (m_vertex != -1)
return mask[index];
// if this vertex is already visited,
// return the bit-mask
// value of this vertex.
if (mask[index] != 0)
return mask[index];
int tmpmask = 0;
// Set the bit corresponding
// to vertex index in tmpmask
tmpmask |= (1 << index);
for (int i = 0; i < n; i++) {
if ((index != i) && IsEdge(adj, index, i)) {
// Set bits corresponding to all
// vertex which can be visited
// by this vertex by ORing
// the return value by util function
// Vertex is not visited
if (mask[i] == 0) {
int retmask = MotherVertexUtil(
adj, i, mask, m_vertex);
tmpmask |= retmask;
}
// Vertex is already visited
else {
tmpmask |= mask[i];
}
// Check if current vertex is
// mother vertex or mother vertex
// is already found
if (tmpmask == Math.Pow((2), n) - 1) {
// If all bits of a mask is set
// it means current vertex
// is mother vertex
if (m_vertex == -1) {
m_vertex = index;
}
return tmpmask;
}
}
}
// populate tmpmask as final
// bit mask of the vertex
mask[index] |= tmpmask;
return mask[index];
}
public static int MotherVertex(List<List<int> > adj)
{
int n = adj.Count();
int[] mask = new int[n];
// Initially bit mask
// for all vertex will be 0
for (int i = 0; i < n; i++) {
mask[i] = 0;
}
// DFS traversal is used to check
// for the mother vertex
// All set bits (of bitmask of a vertex)
// represent the current vertex index
// and index of vertices which could be
// visited from the current vertex.
/* Example:
If a vertex index is 3
then and vertex 5, 7 and 10
can be visited from this vertex
then final bit mask of this vertex
would be
00000000000000000000010010101000
(bits 3, 5, 7 and 10 are set) */
// tmpmask is used to store
// the final bitmask of the vertex.
int tmpmask = 0;
// flag to check if
// mother vertex is found
int m_vertex = -1;
for (int index = 0; index < n; index++) {
// set the bit corresponding
// to vertex index in tmpmask
tmpmask = 1 << index;
// mask for a vertex is 0
// means it has not yet
// visited so visit this vertex
if (mask[index] == 0) {
int retmask = MotherVertexUtil(
adj, index, mask, m_vertex);
// set bits corresponding to all
// vertices which can be visited
// from this vertex by ORing
// the return value by util function
tmpmask |= retmask;
}
// check if current vertex is
// mother vertex or mother vertex
// is already found
// If all bits of a mask is set
// it means current vertex
// is mother vertex
if (tmpmask == Math.Pow((2), n) - 1)
{
// current vertex is mother vertex
if (m_vertex == -1) {
m_vertex = index;
}
break;
}
// populate tmpmask as final bit
// mask of the vertex
mask[index] |= tmpmask;
}
return m_vertex;
}
}
// This code is contributed by Tapesh (tapeshdua420)
There is an edge from 0 to 2 There is an edge from 0 to 1 There is an edge from 1 to 3 There is an edge from 4 to 1 There is an edge from 5 to 2 There is an edge from 5 to 6 There is an edge from 6 to 0 There is an edge from 6 to 4 Mother vertex is: 5
Complejidad temporal: O(V ^ 2), donde V es el número total de vértices del gráfico.
Espacio Auxiliar: O(V)