Pruebas de Bernoulli y Distribución Binomial – Probabilidad

En este artículo, vamos a discutir los ensayos de Bernoulli y la distribución binomial en detalle con los teoremas relacionados. El ensayo de Bernoulli también se conoce como ensayo binomial . En el caso del ensayo de Bernoulli, solo hay dos resultados posibles, pero en el caso de la distribución binomial, obtenemos el número de éxitos en una secuencia de experimentos independientes.

Los juicios de Bernoulli

Consideremos n repeticiones(ensayos) independientes de un experimento aleatorio E. Si A es un evento asociado con E tal que P(A) permanece igual para las repeticiones, los ensayos se denominan ensayos de Bernoulli .

Teorema: si la probabilidad de ocurrencia de un evento (probabilidad de éxito) en una sola prueba del experimento de Bernoulli es p, entonces la probabilidad de que el evento ocurra exactamente r veces de n pruebas independientes es igual a ⁿ C _r q ^{n – r} p ^r, donde q = 1 – p , la probabilidad de falla del evento.

En breve:

Probabilidad requerida = ⁿ C _r q ^{n – r} p ^r

dónde,

p = Probabilidad de Éxito

q = 1 – p = Probabilidad de falla

n = Número de ensayos independientes

r = El número de veces que ocurrió un evento

Prueba:

Obtener exactamente r éxitos significa obtener r éxitos y (n – r) fracasos simultáneamente.

∴ P(obteniendo r éxitos y n – r fracasos) = q ^{n – r} p ^r (ya que los n intentos son independientes) [Teorema del producto]

No se especifican las pruebas de las que se obtienen los éxitos. Hay ⁿ C _r formas de elegir r intentos de éxito. Una vez que los r intentos se eligen como exitosos, los intentos restantes (n – r) deberían dar como resultado fallas . Estas ⁿ C _r formas son mutuamente excluyentes. En cada una de estas ⁿ C _r formas, P(obtener exactamente r éxitos) = q ^{n – r} p ^r

Por lo tanto, por el teorema de la suma, la probabilidad requerida = ⁿ C _r q ^{n – r} p ^r

Generalización del teorema de Bernoulli

Distribución multinomial:

Si A ₁ , A ₂ , . . . , _Ak son eventos exhaustivos y mutuamente excluyentes asociados con un experimento aleatorio tal que, P(A _i ocurre ) = p _i donde,

pag ₁ + pag ₂ +. . . + p _k = 1, y si el experimento se repite n veces, entonces la probabilidad de que A ₁ ocurra r ₁ veces, A ₂ ocurra r ₂ veces,. . . . ,A _k ocurre r _k veces viene dado por:

PAGS _norte (r ₁ , r _{2 , . . . ,} r _k ) = $\frac{n!}{r_{1}! r_{2}! . . . r_{k}!} \ p_{1}^{r_{1}}\times p_{2}^{r_{2}}\times. . .\times p_{k}^{r_{k}}$

dónde,

Prueba:

Los r ₁ intentos en los que ocurre el evento A ₁ pueden elegirse entre los n intentos ⁿ C _r caminos. Los intentos restantes (n – r ₁ ) se dejan para los otros eventos.

Los r ₂ ensayos en los que ocurre el evento A ₂ pueden elegirse entre los (n – r ₁ ) ensayos en ^{(n – r}_¹⁾ C _r2 formas.

Los r ₃ intentos en los que ocurre el evento A ₃ pueden elegirse entre los (n – r ₁ – r ₂ ) intentos en ^{(n – r}_¹^{– r}_²⁾ C _r3 formas, y así sucesivamente.

Por lo tanto, el número de formas en que los eventos pueden ocurrir:

ⁿ C_r₁ ×⁽^norte⁻^r_¹⁾C _r₂ ×⁽^norte⁻^r_¹⁻^r_²⁾C ^r₃ ×⁽_norte⁻^r_¹⁻^r_¹^{– … −}^r_^k^{− 1)}C = n!/(r₁ !r₂ ! . . . r₃ !)

Considere cualquiera de las formas anteriores en las que los eventos A ₁ , A ₂ , . . ., _Ak ocurrir.

Como los n intentos son independientes, r ₁ + r ₂ + . . . +r _k los ensayos también son independientes.

∴ P(A ₁ ocurre r ₁ veces, A ₂ ocurre r ₂ veces, . . . , A _k ocurre r _k veces) = p ₁^r_¹ × p ₂^r_² × . . . × p _k ^r_^k

Dado que las formas en que ocurren los eventos son mutuamente excluyentes, la probabilidad requerida está dada por

PAGS norte (r ₁_, r ₂ , . . . , r _k ) = $\frac{n!}{r_{1}! r_{2}! . . . r_{k}!}$ [Tex]\times \ p_{1} ^{r_{1}}\times p_{2}^{r_{2}}\times… \veces p_{k}^{r_{k}}[/Tex]

Ejemplos

Ejemplo 1: Se lanza una moneda infinitas veces. Si la probabilidad de que salga cara en un solo lanzamiento es p, demuestre que la probabilidad de que la k-ésima cara se obtenga en el n-ésimo lanzamiento, pero no antes, es , donde q = 1 – p.

Solución :

Deben obtenerse K caras en el enésimo lanzamiento, pero no antes.

Por lo tanto, se deben obtener (k – 1) caras en los primeros (n – 1) lanzamientos y 1 cara en el n-ésimo lanzamiento.

Probabilidad requerida = P[ k – 1 cara en (n – 1) lanzamientos] × P(1 cara en 1 lanzamiento)] =

Ejemplo 2: si al menos 1 niño en una familia con 2 niños es un niño, ¿cuál es la probabilidad de que ambos niños sean niños?

Solución:

p = Probabilidad de que un niño sea niño = 1/2.

∴ q = 1/2 y n = 2

P(al menos un niño) = p (exactamente 1 niño) + p (exactamente 2 niños) = $2C_{1}\frac{1}{2}^2 + 2C_{2}\frac{1}{2}^2$ = $\frac{3}{4}$

∴ Probabilidad requerida = P(ambos son niños) / P(al menos 1 niño) = $\frac{1}{4}/\frac{3}{4} = \frac{1}{3}$

Distribución binomial

Teorema: Sea A algún evento asociado con un experimento aleatorio E, tal que P(A) = p y P(A’) = q = 1 – p. Suponiendo que p permanece igual para todas las repeticiones, si consideramos n repeticiones (o ensayos) independientes de E y si la variable aleatoria (RV)X denota el número de veces que ha ocurrido el evento A, entonces X se denomina variable aleatoria binomial con parámetros n y p o podemos decir que X sigue una distribución binomial con parámetros n y p, o simbólicamente B(n, p). Obviamente, los posibles valores que puede tomar X, son 0, 1, 2,…., n. Por el teorema bajo los ensayos de Bernoulli, la función de masa de probabilidad de un RV binomial está dada por

ⁿ C _r q ^{n – r} p ^r , r

Nota:

1. La distribución binomial es una distribución de probabilidad legítima ya que

$\sum_{r=0}^n P(X=r)=\sum_{r=0}^n nCrq^{n-r}p^r=(q+p)^n=1$

2. La Media de la Distribución Binomial viene dada por: $E(x)=\sum_{r} x_{r}p_{r}=np$ ; además $E(x^2)=\sum_{r}x_{r}^2p_{r}$

3.La Varianza de la Distribución Binomial viene dada por: $Var(x)=E(x^2)-{{E(x)}}^2=npq$

Ejemplos

Ejemplo 1: De 800 familias con 4 niños cada una, ¿cuántas familias se esperaría que tuvieran

(i) 2 niños y 2 niñas,

(ii) al menos 1 niño,

(iii) como máximo 2 niñas,

(iv) hijos de ambos sexos.

Suponga probabilidades iguales para niños y niñas.

Solución:

Considerando a cada hijo como una prueba, n = 4. Suponiendo que el nacimiento de un niño es un éxito, p = 1/2 y q = 1/2. Sea X el número de éxitos (niños).

(i) P(2 niños y 2 niñas) = P(X = 2)

= $4C_{2} \times (\frac{1}{2})^2 \times (\frac{1}{2})^{4-2}=6 \times(\frac{1}{2})^4=\frac{3}{8}$

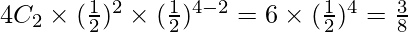
$\therefore$ Nº de familias con 2 niños y 2 niñas

= NP(X = 2) [N es el número total. de familias consideradas]

= $800 \times \frac{3}{8}=300$

(ii) P(al menos 1 niño) = P(X ≥ 1)

= P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)

= 1 – P(X = 0)

= $1-4C_{0} \times(\frac{1}{2})^0\times(\frac{1}{2})^4=1-\frac{1}{16}=\frac{15}{16}$

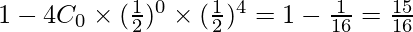
$\therefore$ Nº de familias con al menos 1 niño

= $800 \times \frac{15}{16}=750$

(iii) P(como máximo 2 niñas) = P(exactamente 0 niña, 1 niña o 2 niñas)

= P(X = 4, X = 3 o X = 2)

= $1-(4C_{0} \times (\frac{1}{2})^4+4C_{1} \times(\frac{1}{2})^4)=\frac{11}{16}$

$\therefore$ Nº de familias que tienen como máximo 2 niñas

= $800 \times \frac{11}{16}=550$

(iv) P(hijos de ambos sexos)

= 1 – P( hijos del mismo sexo )

= 1 – {P(todos son niños) + P(todas son niñas)}

= 1 – {P(X = 4) + P(X = 0)}

= $1-(4C_{4} \times(\frac{1}{2})^4 + 4C_{0}\times(\frac{1}{2})^4)=1-\frac{1}{8}=\frac{7}{8}$

$\therefore$ Nº de familias con hijos de ambos sexos

= $800\times\frac{7}{8} = 700$

Ejemplo 2: Se lanzan diez monedas simultáneamente. ¿Encuentre la probabilidad de obtener al menos siete caras?

Solución:

p = Probabilidad de sacar cara = 1/2

q = Probabilidad de no sacar cara = 1 – p = 1/2

La probabilidad de obtener x caras en un lanzamiento aleatorio de 10 monedas es:

p(x) = $10C_{x}\times\frac{1}{2}^x\times\frac{1}{2}^{10-x}=10C_{x}\times\frac{1}{2}^{10}$ ; X = 0, 1, 2, . . . , 10

$\therefore$ La probabilidad de obtener al menos siete caras viene dada por:

P(X ≥ 7) = p(7) + p(8) + p(9) + p(10)

= $\frac{1}{2}^{10}( 10C_{7} + 10C_{8} + 10C_{9} + 10C_{10}) =\frac{176}{1024}$

Publicación traducida automáticamente

Artículo escrito por parkrijimin y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Los juicios de Bernoulli

Generalización del teorema de Bernoulli

Ejemplos

Distribución binomial

Ejemplos

Deja una respuesta Cancelar la respuesta