Estimación de Variables | conjunto 2

Prerrequisito: Estimación de Variable | set 1
Términos relacionados con las métricas de variabilidad: 

-> Deviation 
-> Variance
-> Standard Deviation
-> Mean Absolute Deviation
-> Median Absolute Deviation
-> Order Statistics
-> Range
-> Percentile 
-> Inter-quartile Range

• Desviación absoluta media: la desviación absoluta media, la varianza y la desviación estándar (analizadas en la sección anterior) no son sólidas para valores extremos y valores atípicos. Promediamos la suma de las desviaciones de la mediana. 
   

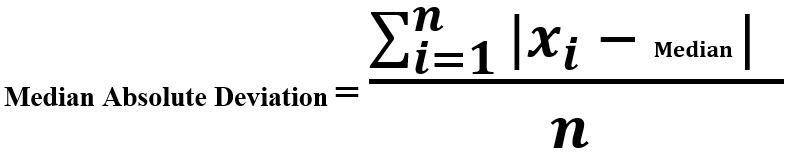
• Ejemplo : 

Sequence : [2, 4, 6, 8] 
Mean     = 5
Deviation around mean = [-3, -1, 1, 3]

Mean Absolute Deviation = (3 + 1 + 1 + 3)/ 4

# Median Absolute Deviation
 
import numpy as np
 
def mad(data):
    return np.median(np.absolute(
            data - np.median(data)))
     
Sequence = [2, 4, 10, 6, 8, 11]
 
print ("Median Absolute Deviation : ", mad(Sequence))
    

Producción : 

Median Absolute Deviation :  3.0

• Estadísticas de orden: este enfoque de medición de la variabilidad se basa en la distribución de datos clasificados (clasificados).
• Rango: Es la medida más básica perteneciente a las Estadísticas de Orden. Es la diferencia entre el valor más grande y el más pequeño del conjunto de datos. Es bueno conocer la dispersión de los datos, pero es muy sensible a los valores atípicos. Podemos mejorarlo eliminando los valores extremos. 
  Ejemplo : 

Sequence : [2, 30, 50, 46, 37, 91]
Here, 2 and 91 are outliers

Range = 91 - 2 = 89
Range without outliers = 50 - 30 = 20

• Percentil: Es una muy buena medida para medir la variabilidad en los datos, evitando valores atípicos. ^{El percentil} P en los datos es un valor tal que al menos P% o menos valores son menores que él y al menos (100 – P)% los valores son más que P. 
  La mediana es el percentil 50 de los datos. 
  Ejemplo : 

Sequence : [2, 30, 50, 46, 37, 91] 
Sorted   : [2, 30, 37, 46, 50, 91]

50th percentile = (37 + 46) / 2 = 41.5 

• Código – 

# Percentile
 
import numpy as np
 
     
Sequence = [2, 30, 50, 46, 37, 91]
 
print ("50th Percentile : ", np.percentile(Sequence, 50))
     
print ("60th Percentile : ", np.percentile(Sequence, 60))

Producción : 

50th Percentile :  41.5
60th Percentile :  46.0

• Rango intercuartílico (IQR): funciona para los datos clasificados (ordenados). Tiene 3 cuartiles que dividen los datos: Q1 (percentil 25 ⁾ , Q2 (percentil 50 ⁾ y Q3 (percentil 75 ⁾ . El rango intercuartílico es la diferencia entre Q3 y Q1. 
  Ejemplo : 

Sequence : [2, 30, 50, 46, 37, 91] 
Q1 (25th percentile) : 31.75
Q2 (50th percentile) : 41.5
Q3 (75th percentile) : 49

IQR = Q3 - Q1 = 17.25

• Código – 1 

# Inter-Quartile Range
 
import numpy as np
from scipy.stats import iqr
     
Sequence = [2, 30, 50, 46, 37, 91]
 
print ("IQR : ", iqr(Sequence))

Producción : 

IQR :  17.25

• Código – 2 

import numpy as np
 
# Inter-Quartile Range
iqr = np.subtract(*np.percentile(Sequence, [75, 25]))
 
print ("\nIQR : ", iqr)

Producción : 

IQR :  17.25