Estimación del valor de Pi usando Monte Carlo

Posted on by Rudeus Greyrat

Estimación de  
Monte Carlo Los métodos de Monte Carlo son una amplia clase de algoritmos computacionales que se basan en muestreos aleatorios repetidos para obtener resultados numéricos. Uno de los ejemplos básicos para comenzar con el algoritmo de Monte Carlo es la estimación de Pi . 
Estimación de Pi 
La idea es simular puntos aleatorios (x, y) en un plano 2-D con dominio como un cuadrado de lado 2r unidades centrado en (0,0). Imagina un círculo dentro del mismo dominio con el mismo radio r e inscrito en el cuadrado. Luego calculamos la proporción del número de puntos que se encuentran dentro del círculo y el número total de puntos generados. Consulte la imagen a continuación:
 

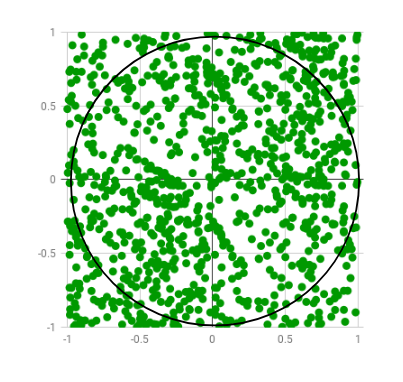
Estimating the value of Pi using Monte Carlo

Se generan puntos aleatorios, solo unos pocos de los cuales se encuentran fuera del círculo imaginario.

Sabemos que el área del cuadrado es la  4r^{2}  unidad cuadrada mientras que la del círculo es  \pi r^{2} . La relación de estas dos áreas es la siguiente:

\frac{\textrm{area of the circle}}{\textrm{area of the square}} = \frac{\pi r^{2}}{4r^{2}} = \frac{\pi}{4}

Ahora, para una gran cantidad de puntos generados, 

\frac{\pi}{4} = \frac{\textrm{no. of points generated inside the circle}}{\textrm{total no. of points generated or no. of points generated inside the square}}that is,\pi = 4 \ast \frac{\textrm{no. of points generated inside the circle}}{\textrm{no. of points generated inside the square}}

La belleza de este algoritmo es que no necesitamos ningún gráfico o simulación para mostrar los puntos generados. Simplemente generamos pares aleatorios (x, y) y luego verificamos si  x^{2} + y^{2} \leqslant 1 . Si es así, incrementamos el número de puntos que aparecen dentro del círculo. En algoritmos aleatorizados y de simulación como Monte Carlo, cuanto mayor sea el número de iteraciones, más preciso será el resultado. Por lo tanto, el título es » Estimación del valor de Pi» y no «Calculación del valor de Pi». A continuación se muestra el algoritmo para el método:
El algoritmo 
1. Inicializa puntos_círculo, puntos_cuadrado e intervalo a 0. 
2. Genera un punto aleatorio x. 
3. Genere un punto aleatorio y. 
4. Calcular d = x*x + y*y. 
5. Si d <= 1, incremente circle_points. 
6. Incremente square_points. 
7. Intervalo de incremento. 
8. Si el incremento < NÚMERO_DE_ITERACIONES, repita desde 2. 
9. Calcule pi = 4*(puntos_círculo/puntos_cuadrado). 
10. Terminar.
El código no espera ninguna entrada a través de stdin ya que el macro INTERVALO podría cambiarse según el número requerido de iteraciones. El número de iteraciones es el cuadrado de INTERVALO. Además, pausé la pantalla durante las primeras 10 iteraciones con getch() y los resultados se muestran para cada iteración con el formato que se indica a continuación. Puede cambiarlos o eliminarlos según sus requisitos. 
 

x y circle_points square_points - pi

Ejemplos:

INTERVAL = 5
Output : Final Estimation of Pi = 2.56

INTERVAL = 10
Output : Final Estimation of Pi = 3.24

INTERVAL = 100
Output : Final Estimation of Pi = 3.0916

C++

/* C++ program for estimation of Pi using Monte
   Carlo Simulation */
#include <bits/stdc++.h>
 
// Defines precision for x and y values. More the
// interval, more the number of significant digits
#define INTERVAL 10000
using namespace std;
 
int main()
{
    int interval, i;
    double rand_x, rand_y, origin_dist, pi;
    int circle_points = 0, square_points = 0;
 
    // Initializing rand()
    srand(time(NULL));
 
    // Total Random numbers generated = possible x
    // values * possible y values
    for (i = 0; i < (INTERVAL * INTERVAL); i++) {
 
        // Randomly generated x and y values
        rand_x = double(rand() % (INTERVAL + 1)) / INTERVAL;
        rand_y = double(rand() % (INTERVAL + 1)) / INTERVAL;
 
        // Distance between (x, y) from the origin
        origin_dist = rand_x * rand_x + rand_y * rand_y;
 
        // Checking if (x, y) lies inside the define
        // circle with R=1
        if (origin_dist <= 1)
            circle_points++;
 
        // Total number of points generated
        square_points++;
 
        // estimated pi after this iteration
        pi = double(4 * circle_points) / square_points;
 
        // For visual understanding (Optional)
        cout << rand_x << " " << rand_y << " "
             << circle_points << " " << square_points
             << " - " << pi << endl
             << endl;
 
        // Pausing estimation for first 10 values (Optional)
        if (i < 20)
            getchar();
    }
 
    // Final Estimated Value
    cout << "\nFinal Estimation of Pi = " << pi;
 
    return 0;
}

Java

// Java program for estimation of Pi using Monte
//Carlo Simulation
import java.util.*;
import java.io.*;
import java.util.concurrent.ThreadLocalRandom;
 
class GFG
{
    // Defines precision for x and y values. More the
    // interval, more the number of significant digits
    static int INTERVAL = 10000;
     
    // Driver code
    public static void main(String[] args)throws IOException
    {
        double rand_x, rand_y, origin_dist, pi=0;
        int circle_points = 0, square_points = 0;
         
        // Total Random numbers generated = possible x
        // values * possible y values
        for (int i = 0; i < (INTERVAL * INTERVAL); i++) {
      
            // Randomly generated x and y values in the range [-1,1]
            rand_x = Math.random()*2-1;
            rand_y = Math.random()*2-1;
      
            // Distance between (x, y) from the origin
            origin_dist = rand_x * rand_x + rand_y * rand_y;
      
            // Checking if (x, y) lies inside the define
            // circle with R=1
            if (origin_dist <= 1)
                circle_points++;
      
            // Total number of points generated
            square_points++;
      
            // estimated pi after this iteration
            pi = ((4.0 * circle_points) / square_points);
      
            // For visual understanding (Optional)
            //System.out.println(rand_x+" "+rand_y+" "+circle_points+" "+square_points+" - "+pi);
        }
      
        // Final Estimated Value
        System.out.println("Final Estimation of Pi = " + pi);
    }
}
 
// This code is contributed by shruti456rawal

Python

import random
 
INTERVAL = 1000
 
circle_points = 0
square_points = 0
 
# Total Random numbers generated= possible x
# values* possible y values
for i in range(INTERVAL**2):
 
    # Randomly generated x and y values from a
    # uniform distribution
    # Range of x and y values is -1 to 1
    rand_x = random.uniform(-1, 1)
    rand_y = random.uniform(-1, 1)
 
    # Distance between (x, y) from the origin
    origin_dist = rand_x**2 + rand_y**2
 
    # Checking if (x, y) lies inside the circle
    if origin_dist <= 1:
        circle_points += 1
 
    square_points += 1
 
    # Estimating value of pi,
    # pi= 4*(no. of points generated inside the
    # circle)/ (no. of points generated inside the square)
    pi = 4 * circle_points / square_points
 
##    print(rand_x, rand_y, circle_points, square_points, "-", pi)
# print("\n")
 
print("Final Estimation of Pi=", pi)

C#

// C# program for estimation of Pi using Monte
// Carlo Simulation
using System;
using System.Collections.Generic;
 
class GFG
{
 
  // Defines precision for x and y values. More the
  // interval, more the number of significant digits
  static int INTERVAL = 10000;
 
  // Driver code
  public static void Main(string[] args)
  {
 
    // Instantiate random number generator using
    // system-supplied value as seed
    var rand = new Random();
    double rand_x, rand_y, origin_dist, pi = 0;
    int circle_points = 0, square_points = 0;
 
    // Total Random numbers generated = possible x
    // values * possible y values
    for (int i = 0; i < (INTERVAL * INTERVAL); i++) {
 
      // Randomly generated x and y values in the
      // range [-1,1]
      rand_x = (double)(rand.Next() % (INTERVAL + 1))
        / INTERVAL;
      rand_y = (double)(rand.Next() % (INTERVAL + 1))
        / INTERVAL;
 
      // Distance between (x, y) from the origin
      origin_dist = rand_x * rand_x + rand_y * rand_y;
 
      // Checking if (x, y) lies inside the define
      // circle with R=1
      if (origin_dist <= 1)
        circle_points++;
 
      // Total number of points generated
      square_points++;
 
      // estimated pi after this iteration
      pi = ((4.0 * circle_points) / square_points);
 
      // For visual understanding (Optional)
      // System.out.println(rand_x+" "+rand_y+"
      // "+circle_points+" "+square_points+" - "+pi);
    }
 
    // Final Estimated Value
    Console.WriteLine("Final Estimation of Pi = " + pi);
  }
}
 
// This code is contributed by phasing17

Producción:  

Final Estimation of Pi = 3.16116

Este artículo es una contribución de Paras Lehana . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente. 

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *