Considere una fila de n monedas de valores v1. . . vn, donde n es par. Jugamos un juego contra un oponente alternando turnos. En cada turno, un jugador selecciona la primera o la última moneda de la fila, la retira de la fila de forma permanente y recibe el valor de la moneda. Determine la máxima cantidad posible de dinero que definitivamente podemos ganar si nos movemos primero.
Nota: el oponente es tan inteligente como el usuario.
Entendamos el problema con algunos ejemplos:
- 5, 3, 7, 10: el usuario recopila el valor máximo como 15 (10 + 5)
- 8, 15, 3, 7: el usuario recopila el valor máximo como 22 (7 + 15)
¿Elegir lo mejor en cada movimiento da una solución óptima? No.
En el segundo ejemplo, así es como se puede terminar el juego:
- …….El usuario elige 8.
…….El oponente elige 15.
…….El usuario elige 7.
…….El oponente elige 3.
El valor total recopilado por el usuario es 15 (8 + 7) - …….El usuario elige 7.
…….El oponente elige 8.
…….El usuario elige 15.
…….El oponente elige 3.
El valor total recopilado por el usuario es 22 (7 + 15)
Entonces, si el usuario sigue el segundo estado del juego, se puede recolectar el valor máximo aunque el primer movimiento no sea el mejor.
Enfoque: como ambos jugadores son igualmente fuertes, ambos intentarán reducir la posibilidad de ganar el uno al otro. Ahora veamos cómo el oponente puede lograr esto.
Hay dos opciones:
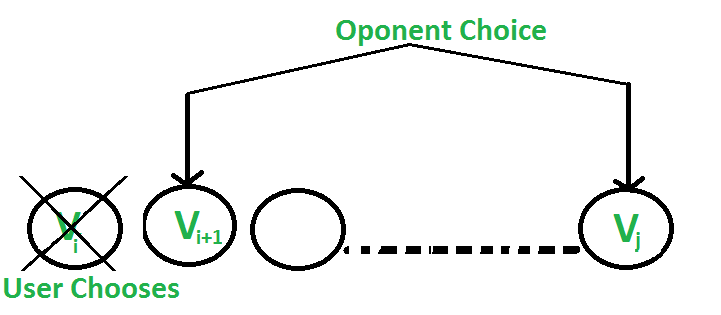
- El usuario elige la ‘ésima’ moneda con el valor ‘Vi’: El oponente elige la (i+1)-ésima moneda o la j-ésima moneda. El oponente tiene la intención de elegir la moneda que deja al usuario con el valor mínimo .
es decir, el usuario puede recopilar el valor Vi + min(F(i+2, j), F(i+1, j-1) ) donde [i+2,j] es el rango de índices de array disponibles para el usuario si el oponente elige Vi+1 y [i+1,j-1] es el rango de índices de array disponibles si el oponente elige la j-ésima moneda.
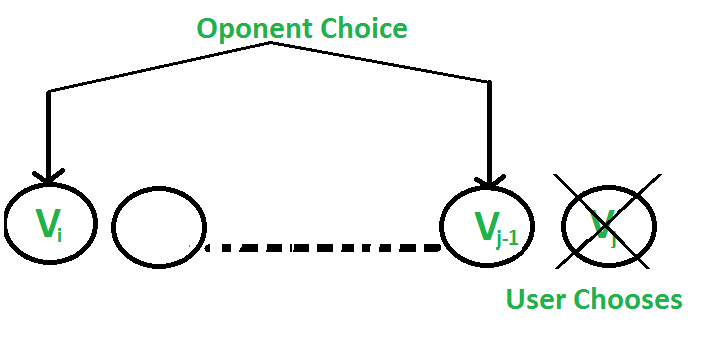
- El usuario elige la moneda ‘jth’ con valor ‘Vj’: El oponente elige la moneda ‘ith’ o la moneda ‘(j-1)th’. El oponente tiene la intención de elegir la moneda que deja al usuario con el valor mínimo, es decir, el usuario puede recoger el valor Vj + min(F(i+1, j-1), F(i, j-2)) donde [i, j-2] es el rango de índices de array disponibles para el usuario si el oponente toma la j-ésima moneda y [i+1,j-1] es el rango de índices disponibles para el usuario si el oponente toma la i-ésima moneda.
La siguiente es la solución recursiva que se basa en las dos opciones anteriores. Tomamos un máximo de dos opciones.
F(i, j) represents the maximum value the user
can collect from i'th coin to j'th coin.
F(i, j) = Max(Vi + min(F(i+2, j), F(i+1, j-1) ),
Vj + min(F(i+1, j-1), F(i, j-2) ))
As user wants to maximise the number of coins.
Base Cases
F(i, j) = Vi If j == i
F(i, j) = max(Vi, Vj) If j == i + 1
La solución recursiva de arriba hacia abajo se muestra a continuación
C++
// C++ code to implement the approach
#include <bits/stdc++.h>
using namespace std;
vector<int> arr;
map<vector<int>, int> memo;
int n = arr.size();
// recursive top down memoized solution
int solve(int i, int j)
{
if ((i > j) || (i >= n) || (j < 0))
return 0;
vector<int> k{ i, j };
if (memo[k] != 0)
return memo[k];
// if the user chooses ith coin, the opponent can choose
// from i+1th or jth coin. if he chooses i+1th coin,
// user is left with [i+2,j] range. if opp chooses jth
// coin, then user is left with [i+1,j-1] range to
// choose from. Also opponent tries to choose in such a
// way that the user has minimum value left.
int option1
= arr[i]
+ min(solve(i + 2, j), solve(i + 1, j - 1));
// if user chooses jth coin, opponent can choose ith
// coin or j-1th coin. if opp chooses ith coin,user can
// choose in range [i+1,j-1]. if opp chooses j-1th coin,
// user can choose in range [i,j-2].
int option2
= arr[j]
+ min(solve(i + 1, j - 1), solve(i, j - 2));
// since the user wants to get maximum money
memo[k] = max(option1, option2);
return memo[k];
}
int optimalStrategyOfGame()
{
memo.clear();
return solve(0, n - 1);
}
// Driver code
int main()
{
arr.push_back(8);
arr.push_back(15);
arr.push_back(3);
arr.push_back(7);
n = arr.size();
cout << optimalStrategyOfGame() << endl;
arr.clear();
arr.push_back(2);
arr.push_back(2);
arr.push_back(2);
arr.push_back(2);
n = arr.size();
cout << optimalStrategyOfGame() << endl;
arr.clear();
arr.push_back(20);
arr.push_back(30);
arr.push_back(2);
arr.push_back(2);
arr.push_back(2);
arr.push_back(10);
n = arr.size();
cout << optimalStrategyOfGame() << endl;
}
// This code is contributed by phasing17
Java
// Java code to implement the approach
import java.util.*;
class GFG {
static ArrayList<Integer> arr = new ArrayList<>();
static HashMap<ArrayList<Integer>, Integer> memo
= new HashMap<>();
static int n = 0;
// recursive top down memoized solution
static int solve(int i, int j)
{
if ((i > j) || (i >= n) || (j < 0))
return 0;
ArrayList<Integer> k = new ArrayList<Integer>();
k.add(i);
k.add(j);
if (memo.containsKey(k))
return memo.get(k);
// if the user chooses ith coin, the opponent can
// choose from i+1th or jth coin. if he chooses
// i+1th coin, user is left with [i+2,j] range. if
// opp chooses jth coin, then user is left with
// [i+1,j-1] range to choose from. Also opponent
// tries to choose in such a way that the user has
// minimum value left.
int option1 = arr.get(i)
+ Math.min(solve(i + 2, j),
solve(i + 1, j - 1));
// if user chooses jth coin, opponent can choose ith
// coin or j-1th coin. if opp chooses ith coin,user
// can choose in range [i+1,j-1]. if opp chooses
// j-1th coin, user can choose in range [i,j-2].
int option2 = arr.get(j)
+ Math.min(solve(i + 1, j - 1),
solve(i, j - 2));
// since the user wants to get maximum money
memo.put(k, Math.max(option1, option2));
return memo.get(k);
}
static int optimalStrategyOfGame()
{
memo.clear();
return solve(0, n - 1);
}
// Driver code
public static void main(String[] args)
{
arr.add(8);
arr.add(15);
arr.add(3);
arr.add(7);
n = arr.size();
System.out.println(optimalStrategyOfGame());
arr.clear();
arr.add(2);
arr.add(2);
arr.add(2);
arr.add(2);
n = arr.size();
System.out.println(optimalStrategyOfGame());
arr.clear();
arr.add(20);
arr.add(30);
arr.add(2);
arr.add(2);
arr.add(2);
arr.add(10);
n = arr.size();
System.out.println(optimalStrategyOfGame());
}
}
// This code is contributed by phasing17
Python3
def optimalStrategyOfGame(arr, n):
memo = {}
# recursive top down memoized solution
def solve(i, j):
if i > j or i >= n or j < 0:
return 0
k = (i, j)
if k in memo:
return memo[k]
# if the user chooses ith coin, the opponent can choose from i+1th or jth coin.
# if he chooses i+1th coin, user is left with [i+2,j] range.
# if opp chooses jth coin, then user is left with [i+1,j-1] range to choose from.
# Also opponent tries to choose
# in such a way that the user has minimum value left.
option1 = arr[i] + min(solve(i+2, j), solve(i+1, j-1))
# if user chooses jth coin, opponent can choose ith coin or j-1th coin.
# if opp chooses ith coin,user can choose in range [i+1,j-1].
# if opp chooses j-1th coin, user can choose in range [i,j-2].
option2 = arr[j] + min(solve(i+1, j-1), solve(i, j-2))
# since the user wants to get maximum money
memo[k] = max(option1, option2)
return memo[k]
return solve(0, n-1)
C#
// C# code to implement the approach
using System;
using System.Collections.Generic;
class GFG {
static List<int> arr = new List<int>();
static Dictionary<List<int>, int> memo
= new Dictionary<List<int>, int>();
static int n = 0;
// recursive top down memoized solution
static int solve(int i, int j)
{
if ((i > j) || (i >= n) || (j < 0))
return 0;
List<int> k = new List<int>{ i, j };
if (memo.ContainsKey(k))
return memo[k];
// if the user chooses ith coin, the opponent can
// choose from i+1th or jth coin. if he chooses
// i+1th coin, user is left with [i+2,j] range. if
// opp chooses jth coin, then user is left with
// [i+1,j-1] range to choose from. Also opponent
// tries to choose in such a way that the user has
// minimum value left.
int option1 = arr[i]
+ Math.Min(solve(i + 2, j),
solve(i + 1, j - 1));
// if user chooses jth coin, opponent can choose ith
// coin or j-1th coin. if opp chooses ith coin,user
// can choose in range [i+1,j-1]. if opp chooses
// j-1th coin, user can choose in range [i,j-2].
int option2 = arr[j]
+ Math.Min(solve(i + 1, j - 1),
solve(i, j - 2));
// since the user wants to get maximum money
memo[k] = Math.Max(option1, option2);
return memo[k];
}
static int optimalStrategyOfGame()
{
memo.Clear();
return solve(0, n - 1);
}
// Driver code
public static void Main(string[] args)
{
arr.Add(8);
arr.Add(15);
arr.Add(3);
arr.Add(7);
n = arr.Count;
Console.WriteLine(optimalStrategyOfGame());
arr.Clear();
arr.Add(2);
arr.Add(2);
arr.Add(2);
arr.Add(2);
n = arr.Count;
Console.WriteLine(optimalStrategyOfGame());
arr.Clear();
arr.Add(20);
arr.Add(30);
arr.Add(2);
arr.Add(2);
arr.Add(2);
arr.Add(10);
n = arr.Count;
Console.WriteLine(optimalStrategyOfGame());
}
}
// This code is contributed by phasing17
Javascript
// JavaScript code to implement the approach
function optimalStrategyOfGame(arr, n)
{
let memo = {};
// recursive top down memoized solution
function solve(i, j)
{
if ( (i > j) || (i >= n) || (j < 0))
return 0;
let k = (i, j);
if (memo.hasOwnProperty(k))
return memo[k];
// if the user chooses ith coin, the opponent can choose from i+1th or jth coin.
// if he chooses i+1th coin, user is left with [i+2,j] range.
// if opp chooses jth coin, then user is left with [i+1,j-1] range to choose from.
// Also opponent tries to choose
// in such a way that the user has minimum value left.
let option1 = arr[i] + Math.min(solve(i+2, j), solve(i+1, j-1));
// if user chooses jth coin, opponent can choose ith coin or j-1th coin.
// if opp chooses ith coin,user can choose in range [i+1,j-1].
// if opp chooses j-1th coin, user can choose in range [i,j-2].
let option2 = arr[j] + Math.min(solve(i+1, j-1), solve(i, j-2));
// since the user wants to get maximum money
memo[k] = Math.max(option1, option2);
return memo[k];
}
return solve(0, n-1);
}
// Driver code
let arr1 = [ 8, 15, 3, 7 ];
let n = arr1.length;
console.log(optimalStrategyOfGame(arr1, n));
let arr2 = [ 2, 2, 2, 2 ];
n = arr2.length;
console.log(optimalStrategyOfGame(arr2, n));
let arr3 = [ 20, 30, 2, 2, 2, 10 ];
n = arr3.length;
console.log(optimalStrategyOfGame(arr3, n));
// This code is contributed by phasing17
El enfoque de abajo hacia arriba se muestra a continuación.
C++
// C++ program to find out
// maximum value from a given
// sequence of coins
#include <bits/stdc++.h>
using namespace std;
// Returns optimal value possible
// that a player can collect from
// an array of coins of size n.
// Note than n must be even
int optimalStrategyOfGame(int* arr, int n)
{
// Create a table to store
// solutions of subproblems
int table[n][n];
// Fill table using above
// recursive formula. Note
// that the table is filled
// in diagonal fashion (similar
// to http:// goo.gl/PQqoS),
// from diagonal elements to
// table[0][n-1] which is the result.
for (int gap = 0; gap < n; ++gap) {
for (int i = 0, j = gap; j < n; ++i, ++j) {
// Here x is value of F(i+2, j),
// y is F(i+1, j-1) and
// z is F(i, j-2) in above recursive
// formula
int x = ((i + 2) <= j) ? table[i + 2][j] : 0;
int y = ((i + 1) <= (j - 1))
? table[i + 1][j - 1]
: 0;
int z = (i <= (j - 2)) ? table[i][j - 2] : 0;
table[i][j] = max(arr[i] + min(x, y),
arr[j] + min(y, z));
}
}
return table[0][n - 1];
}
// Driver program to test above function
int main()
{
int arr1[] = { 8, 15, 3, 7 };
int n = sizeof(arr1) / sizeof(arr1[0]);
printf("%d\n", optimalStrategyOfGame(arr1, n));
int arr2[] = { 2, 2, 2, 2 };
n = sizeof(arr2) / sizeof(arr2[0]);
printf("%d\n", optimalStrategyOfGame(arr2, n));
int arr3[] = { 20, 30, 2, 2, 2, 10 };
n = sizeof(arr3) / sizeof(arr3[0]);
printf("%d\n", optimalStrategyOfGame(arr3, n));
return 0;
}
Java
// Java program to find out maximum
// value from a given sequence of coins
import java.io.*;
class GFG {
// Returns optimal value possible
// that a player can collect from
// an array of coins of size n.
// Note than n must be even
static int optimalStrategyOfGame(int arr[], int n)
{
// Create a table to store
// solutions of subproblems
int table[][] = new int[n][n];
int gap, i, j, x, y, z;
// Fill table using above recursive formula.
// Note that the tableis filled in diagonal
// fashion (similar to http:// goo.gl/PQqoS),
// from diagonal elements to table[0][n-1]
// which is the result.
for (gap = 0; gap < n; ++gap) {
for (i = 0, j = gap; j < n; ++i, ++j) {
// Here x is value of F(i+2, j),
// y is F(i+1, j-1) and z is
// F(i, j-2) in above recursive formula
x = ((i + 2) <= j) ? table[i + 2][j] : 0;
y = ((i + 1) <= (j - 1))
? table[i + 1][j - 1]
: 0;
z = (i <= (j - 2)) ? table[i][j - 2] : 0;
table[i][j]
= Math.max(arr[i] + Math.min(x, y),
arr[j] + Math.min(y, z));
}
}
return table[0][n - 1];
}
// Driver program
public static void main(String[] args)
{
int arr1[] = { 8, 15, 3, 7 };
int n = arr1.length;
System.out.println(
"" + optimalStrategyOfGame(arr1, n));
int arr2[] = { 2, 2, 2, 2 };
n = arr2.length;
System.out.println(
"" + optimalStrategyOfGame(arr2, n));
int arr3[] = { 20, 30, 2, 2, 2, 10 };
n = arr3.length;
System.out.println(
"" + optimalStrategyOfGame(arr3, n));
}
}
// This code is contributed by vt_m
Python3
# Python3 program to find out maximum # value from a given sequence of coins # Returns optimal value possible that # a player can collect from an array # of coins of size n. Note than n # must be even def optimalStrategyOfGame(arr, n): # Create a table to store # solutions of subproblems table = [[0 for i in range(n)] for i in range(n)] # Fill table using above recursive # formula. Note that the table is # filled in diagonal fashion # (similar to http://goo.gl / PQqoS), # from diagonal elements to # table[0][n-1] which is the result. for gap in range(n): for j in range(gap, n): i = j - gap # Here x is value of F(i + 2, j), # y is F(i + 1, j-1) and z is # F(i, j-2) in above recursive # formula x = 0 if((i + 2) <= j): x = table[i + 2][j] y = 0 if((i + 1) <= (j - 1)): y = table[i + 1][j - 1] z = 0 if(i <= (j - 2)): z = table[i][j - 2] table[i][j] = max(arr[i] + min(x, y), arr[j] + min(y, z)) return table[0][n - 1] # Driver Code arr1 = [8, 15, 3, 7] n = len(arr1) print(optimalStrategyOfGame(arr1, n)) arr2 = [2, 2, 2, 2] n = len(arr2) print(optimalStrategyOfGame(arr2, n)) arr3 = [20, 30, 2, 2, 2, 10] n = len(arr3) print(optimalStrategyOfGame(arr3, n)) # This code is contributed # by sahilshelangia
C#
// C# program to find out maximum
// value from a given sequence of coins
using System;
public class GFG {
// Returns optimal value possible that a player
// can collect from an array of coins of size n.
// Note than n must be even
static int optimalStrategyOfGame(int[] arr, int n)
{
// Create a table to store solutions of subproblems
int[, ] table = new int[n, n];
int gap, i, j, x, y, z;
// Fill table using above recursive formula.
// Note that the tableis filled in diagonal
// fashion (similar to http:// goo.gl/PQqoS),
// from diagonal elements to table[0][n-1]
// which is the result.
for (gap = 0; gap < n; ++gap) {
for (i = 0, j = gap; j < n; ++i, ++j) {
// Here x is value of F(i+2, j),
// y is F(i+1, j-1) and z is
// F(i, j-2) in above recursive formula
x = ((i + 2) <= j) ? table[i + 2, j] : 0;
y = ((i + 1) <= (j - 1))
? table[i + 1, j - 1]
: 0;
z = (i <= (j - 2)) ? table[i, j - 2] : 0;
table[i, j]
= Math.Max(arr[i] + Math.Min(x, y),
arr[j] + Math.Min(y, z));
}
}
return table[0, n - 1];
}
// Driver program
static public void Main()
{
int[] arr1 = { 8, 15, 3, 7 };
int n = arr1.Length;
Console.WriteLine(""
+ optimalStrategyOfGame(arr1, n));
int[] arr2 = { 2, 2, 2, 2 };
n = arr2.Length;
Console.WriteLine(""
+ optimalStrategyOfGame(arr2, n));
int[] arr3 = { 20, 30, 2, 2, 2, 10 };
n = arr3.Length;
Console.WriteLine(""
+ optimalStrategyOfGame(arr3, n));
}
}
// This code is contributed by ajit
PHP
<?php
// PHP program to find out maximum value
// from a given sequence of coins
// Returns optimal value possible that a
// player can collect from an array of
// coins of size n. Note than n must be even
function optimalStrategyOfGame($arr, $n)
{
// Create a table to store solutions
// of subproblems
$table = array_fill(0, $n,
array_fill(0, $n, 0));
// Fill table using above recursive formula.
// Note that the table is filled in diagonal
// fashion (similar to http://goo.gl/PQqoS),
// from diagonal elements to table[0][n-1]
// which is the result.
for ($gap = 0; $gap < $n; ++$gap)
{
for ($i = 0, $j = $gap; $j < $n; ++$i, ++$j)
{
// Here x is value of F(i+2, j),
// y is F(i+1, j-1) and z is F(i, j-2)
// in above recursive formula
$x = (($i + 2) <= $j) ?
$table[$i + 2][$j] : 0;
$y = (($i + 1) <= ($j - 1)) ?
$table[$i + 1][$j - 1] : 0;
$z = ($i <= ($j - 2)) ?
$table[$i][$j - 2] : 0;
$table[$i][$j] = max($arr[$i] + min($x, $y),
$arr[$j] + min($y, $z));
}
}
return $table[0][$n - 1];
}
// Driver Code
$arr1 = array( 8, 15, 3, 7 );
$n = count($arr1);
print(optimalStrategyOfGame($arr1, $n) . "\n");
$arr2 = array( 2, 2, 2, 2 );
$n = count($arr2);
print(optimalStrategyOfGame($arr2, $n) . "\n");
$arr3 = array(20, 30, 2, 2, 2, 10);
$n = count($arr3);
print(optimalStrategyOfGame($arr3, $n) . "\n");
// This code is contributed by chandan_jnu
?>
Javascript
<script>
// Javascript program to find out maximum
// value from a given sequence of coins
// Returns optimal value possible
// that a player can collect from
// an array of coins of size n.
// Note than n must be even
function optimalStrategyOfGame(arr, n)
{
// Create a table to store
// solutions of subproblems
let table = new Array(n);
let gap, i, j, x, y, z;
for(let d = 0; d < n; d++)
{
table[d] = new Array(n);
}
// Fill table using above recursive formula.
// Note that the tableis filled in diagonal
// fashion (similar to http:// goo.gl/PQqoS),
// from diagonal elements to table[0][n-1]
// which is the result.
for(gap = 0; gap < n; ++gap)
{
for(i = 0, j = gap; j < n; ++i, ++j)
{
// Here x is value of F(i+2, j),
// y is F(i+1, j-1) and z is
// F(i, j-2) in above recursive formula
x = ((i + 2) <= j) ? table[i + 2][j] : 0;
y = ((i + 1) <= (j - 1)) ?
table[i + 1][j - 1] : 0;
z = (i <= (j - 2)) ? table[i][j - 2] : 0;
table[i][j] = Math.max(
arr[i] + Math.min(x, y),
arr[j] + Math.min(y, z));
}
}
return table[0][n - 1];
}
// Driver code
let arr1 = [ 8, 15, 3, 7 ];
let n = arr1.length;
document.write("" + optimalStrategyOfGame(arr1, n) +
"</br>");
let arr2 = [ 2, 2, 2, 2 ];
n = arr2.length;
document.write("" + optimalStrategyOfGame(arr2, n) +
"</br>");
let arr3 = [ 20, 30, 2, 2, 2, 10 ];
n = arr3.length;
document.write("" + optimalStrategyOfGame(arr3, n));
// This code is contributed by divyesh072019
</script>
22 4 42
Análisis de Complejidad:
- Complejidad Temporal: O(n 2 ).
El uso de un bucle for anidado lleva la complejidad del tiempo a n 2 . - Espacio Auxiliar: O(n 2 ).
Como una tabla 2-D se usa para almacenar estados.
Nota: La solución anterior se puede optimizar utilizando menos comparaciones para cada opción. Consulte más adelante. estrategia óptima para un juego | conjunto 2
Ejercicio:
sus pensamientos sobre la estrategia cuando el usuario desea ganar solo en lugar de ganar con el valor máximo. Al igual que el problema anterior, el número de monedas es par.
¿Puede el enfoque Greedy funcionar bastante bien y dar una solución óptima? ¿Cambiará tu respuesta si el número de monedas es impar? Consulte Juego de monedas de dos esquinas
. Este artículo está compilado por Aashish Barnwal . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA