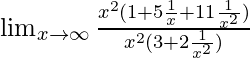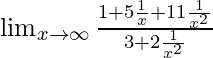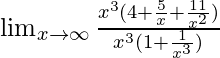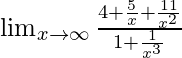Estrategia en la búsqueda de límites

Los límites han sido muy útiles en el campo del cálculo, se convierten en una base sólida para definir muchos conceptos como continuidad, derivabilidad, integrales y derivadas. Estos conceptos nos ayudan aún más a analizar muchas funciones y su comportamiento en el cálculo. Los límites han sido la base de casi todos los conceptos del cálculo. Por lo tanto, se vuelve esencial aprender a calcular los límites para diferentes tipos de funciones y cómo lidiar con las formas indeterminadas de los límites. Veamos diferentes métodos que nos ayudan a calcular los límites de funciones y expresiones complejas.

Límites

Considere una función f(x), y un punto x = c, el límite en este punto se define como el valor que la función parece tomar cuando uno se acerca a este valor de x = c desde el lado izquierdo o derecho. -lado. El límite de la función en un punto particular se define como,

$\lim_{x \to a}f(x)$

La mayoría de los límites se pueden calcular por simple sustitución del punto x = a en la función. Esto se llama el método de sustitución directa. A veces, al calcular los límites, podemos encontrar algunas expresiones que no están definidas. Estas son formas indeterminadas del límite.

Por ejemplo, consideremos una función f(x) = $\frac{x - 2}{x^2 - 4}$ . El objetivo es encontrar el límite de esta función en x = 2.

$\lim_{x \to 2} \frac{x - 2}{x^2 - 4}$

Note que por sustitución directa, este límite toma la forma 0/0. Esta es indefinida y se llama forma indeterminada. De manera similar, ∞/∞, 1 ^∞ también se denominan formas indeterminadas. Para resolver tales formularios, se emplean una serie de estrategias.

Estrategias de Resolución de Límites

Hay varias estrategias y métodos utilizados para encontrar los límites de la función. Qué método se utilizará para qué función depende de varios factores. Por ejemplo, el tipo de función (trigonométrica, exponencial, polinómica, etc.), la forma indeterminada encontrada (∞/∞, 1 ^∞ , 0/0, etc.). No hay reglas establecidas para estas cosas, uno debe practicar, y viene con la experiencia a medida que uno va resolviendo límites para diferentes tipos de funciones. Veamos algunas estrategias para resolver límites.

Sustitución Directa

Muchos de los límites se pueden evaluar simplemente sustituyendo el valor del punto en la función. La condición necesaria para usar este enfoque es que la función debe ser continua y el límite no debe dar una forma indeterminada como salida.

Ejemplo: Considere una función f(x) = x ² + 4x + 13. Halle $\lim_{x \to 1}f(x)$

Solución:

$\lim_{x \to 1}f(x)$

⇒ $\lim_{x \to 1}x^2 + 4x + 13$

⇒ $\lim_{x \to 1}1^2 + 4(1) + 13$

⇒1 +4 + 13

⇒ 18

Factorización y Cancelación

A veces, en algunas funciones, cuando se usa el método de sustitución, el límite toma la forma de 0/0. A menudo, en estos casos, hay algunos factores comunes en el numerador y el denominador que se pueden factorizar y cancelar.

Ejemplo: Considere una función f(x) = $\frac{x - 2}{x^2 - 4}$ . Encontrar $\lim_{x \to 2}f(x)$

Solución:

$\lim_{x \to 2}f(x)$

⇒ $\lim_{x \to 2}\frac{x - 2}{x^2 - 4}$

Usando el método de sustitución,

$\lim_{x \to 2}\frac{2 - 2}{2^2 - 4}$

⇒ $\lim_{x \to 2}\frac{0}{0}$

Ahora usando el método de factorización y cancelación.

⇒ $\lim_{x \to 2}\frac{x - 2}{(x - 2)(x + 2)}$

⇒ $\lim_{x \to 2}\frac{1}{(x + 2)}$

⇒ $\frac{1}{4}$

Caso especial con función seno

A veces, al evaluar la forma 0/0, si la función seno está presente. Esta identidad, $\lim_{x \to 0}\frac{sin(x)}{x} = 1$ viene muy bien.

Ejemplo: Considere una función f(x) = $\frac{4sin(5x)}{3x}$ . Encontrar $\lim_{x \to 0}f(x)$

Solución:

Este límite es de la forma 0/0.

$\lim_{x \to 0}f(x)$

⇒ $\lim_{x \to 0}\frac{4sin(5x)}{3x}$

⇒ $\lim_{x \to 0}\frac{4(5)sin(5x)}{3(5x)}$

⇒ $\frac{20}{3}\lim_{x \to 0}\frac{sin(5x)}{(5x)}$

Usando la identidad mencionada anteriormente,

⇒ $\frac{20}{3}$

Multiplicar por el recíproco de la potencia máxima

En el caso de ∞/∞ forma en los límites y funciones polinómicas. Este método se puede utilizar para resolver el límite. En este caso, tanto el numerador como el denominador se dividen por la mayor potencia de x que aparece en la función.

Ejemplo: Considere una función f(x) = $\frac{x^2 + 5x + 11}{3x^2 + 2 }$ . Encontrar $\lim_{x \to \infty }f(x)$

Solución:

Este límite es de la forma ∞/∞.

$\lim_{x \to \infty }f(x)$

⇒ $\lim_{x \to \infty }\frac{x^2 + 5x + 11}{3x^2 + 2 }$

⇒ $\lim_{x \to \infty }\frac{x^2(1 + 5\frac{1}{x} + 11\frac{1}{x^2})}{x^2(3 + 2\frac{1}{x^2}) }$

⇒ $\lim_{x \to \infty }\frac{1 + 5\frac{1}{x} + 11\frac{1}{x^2}}{3 + 2\frac{1}{x^2} }$

⇒ $\frac{1 + 5(0) + 11(0)}{3 + 2(0) }$

⇒ $\frac{1}{3}$

Regla de L’Hospital

Esta regla es útil para formas indeterminadas como 0/0 o ∞/∞. No hay límite en la clase de funciones en las que se puede aplicar. Se puede aplicar para cualquier tipo de función que evalúe en formas indeterminadas con el método de sustitución. En esta regla, el numerador y el denominador se diferencian hasta que el límite viene en la forma determinada.

Ejemplo: La función mencionada anteriormente, f(x) = $\frac{x - 2}{x^2 - 4}$ . Descubre el $\lim_{x \to 2}f(x)$ uso de la regla de L’Hospital.

Solución:

$\lim_{x \to 2}f(x)$

$\lim_{x \to 2}\frac{x - 2}{x^2 - 4}$

Diferenciar el numerador y el denominador.

$\lim_{x \to 2}\frac{1 }{2x}$

Ahora bien, este límite no está en forma indeterminada,

$\lim_{x \to 2}\frac{1 }{2(2)}$

⇒ $\frac{1}{4}$

Veamos algunos ejemplos más de estos métodos.

Problemas de muestra

Pregunta 1: Considere una función f(x) = x ³ + 4x ² + 1. Halle $\lim_{x \to 1}f(x)$

Solución:

$\lim_{x \to 1}f(x)$

⇒ $\lim_{x \to 1}x^3 + 4x^2+ 1$

⇒ $\lim_{x \to 1}(1)^3 + 4(1)^2+ 1$

⇒1 + 4 + 1

⇒ 6

Pregunta 2: Considere una función f(x) = $\frac{x^2 - 5x + 6}{x- 2}$ . Encontrar $\lim_{x \to 2}f(x)$

Solución:

$\lim_{x \to 2}f(x)$

⇒ $\lim_{x \to 2}\frac{x^2 - 5x + 6}{x- 2}$

Usando el método de sustitución,

$\lim_{x \to 2}\frac{2^2 - 5(2) + 6}{2- 2}$

⇒ $\lim_{x \to 2}\frac{0}{0}$

Ahora usando el método de factorización y cancelación.

⇒ $\lim_{x \to 2}\frac{(x - 2)(x - 3)}{x- 2}$

⇒ $\lim_{x \to 2}\frac{(x - 3)}{1}$

⇒ -1

Pregunta 3: Considere una función f(x) = $\frac{4x^3 + 5x^2 + 11x}{x^3 + 1}$ . Encontrar $\lim_{x \a \infty}f(x)$

Solución:

Este límite es de la forma ∞/∞.

$\lim_{x \a \infty}f(x)$

⇒ $\lim_{x \a \infty}\frac{4x^3 + 5x^2 + 11x}{x^3 + 1}$

⇒ $\lim_{x \to \infty }\frac{x^3(4 + \frac{5}{x} + \frac{11}{x^2})}{x^3(1 +\frac{1 {x^3}) }$

⇒ $\lim_{x \to \infty }\frac{4 + \frac{5}{x} + \frac{11}{x^2}}{1 +\frac{1}{x^3}}$

⇒ 4

Pregunta 4: La función mencionada anteriormente, f(x) = $\frac{e^x - 1}{5x}$ . Descubre el $\lim_{x \to 0}f(x)$ uso de la regla de L’Hospital.

Solución:

$\lim_{x \to 0}f(x)$

$\lim_{x \to 0}\frac{e^x - 1}{5x}$

Diferenciar el numerador y el denominador.

$\lim_{x \to 0}\frac{e^x}{5}$

Ahora bien, este límite no está en forma indeterminada,

$\lim_{x \to 0}\frac{1}{5}$

⇒ $\frac{1}{5}$

Pregunta 5: Considere una función f(x) = $\frac{x^2 - 10x + 24}{x^2 - x +12}$ . Encontrar $\lim_{x \to 4}f(x)$

Solución:

Este límite es de la forma ∞/∞.

$\lim_{x \to \infty }f(x)$

⇒ $\lim_{x \to 4}\frac{x^2 - 10x + 24}{x^2 - x +12 }$

⇒ $\lim_{x \to 4}\frac{x^2 - 6x -4x + 24}{x^2 -4x + 3x +12 }$

⇒ $\lim_{x \to 4}\frac{(x- 6)(x -4)}{(x -4)(x +3) }$

⇒ $\lim_{x \to 4}\frac{x-6}{x +3}$

⇒ $\lim_{x \to 4}\frac{4-6}{4 +3}$

⇒ $\frac{-2}{7}$

Pregunta 6: Considere una función f(x) = $\frac{x^2 - 10x + 24}{x^2 - x +12}$ . Encontrar $\lim_{x \to 4}f(x)$

Solución:

Este límite es de la forma ∞/∞.

$\lim_{x \to \infty }f(x)$

⇒ $\lim_{x \to 4}\frac{x^2 - 10x + 24}{x^2 - x +12 }$

⇒ $\lim_{x \to 4}\frac{x^2 - 6x -4x + 24}{x^2 -4x + 3x +12 }$

⇒ $\lim_{x \to 4}\frac{(x- 6)(x -4)}{(x -4)(x +3) }$

⇒ $\lim_{x \to 4}\frac{x-6}{x +3}$

⇒ $\lim_{x \to 4}\frac{4-6}{4 +3}$

⇒ $\frac{-2}{7}$

Pregunta 7: Considere una función f(x) = $\frac{9x - 1}{3\sqrt{x} - 1}$ . Encontrar $\lim_{x \to \frac{1}{9}}f(x)$

Solución:

Este límite es de la forma ∞/∞.

$\lim_{x \to \frac{1}{9}}f(x)$

⇒ $\lim_{x \to \frac{1}{9}}\frac{9x - 1}{3\sqrt{x} - 1}$

⇒ $\lim_{x \to \frac{1}{9}}\frac{9(x - \frac{1}{9})}{3(\sqrt{x} - \frac{1}{3})}$

⇒ $\lim_{x \to \frac{1}{9}}\frac{9(\sqrt{x} - \frac{1}{3})(\sqrt{x} + \frac{1}{3})}{3(\sqrt{x} - \frac{1}{3})}$

⇒ $\lim_{x \to \frac{1}{9}}\frac{9(\sqrt{x} + \frac{1}{3})}{3}$

⇒ $\lim_{x \to \frac{1}{9}}\frac{3(\sqrt{\frac{1}{9}} + \frac{1}{3})}{1}$

⇒ $\frac{3(\frac{1}{3} + \frac{1}{3})}{1}$

⇒ 2