La integración, como su nombre indica, se utiliza para integrar algo. En matemáticas, la integración es el método utilizado para integrar funciones. La otra palabra para integración puede ser suma como se usa, para resumir, la función completa o de forma gráfica, se usa para encontrar el área bajo la función de la curva. Se sabe que la integración es lo opuesto a la diferenciación, que es el proceso de dividir una función en funciones más pequeñas, mientras que la integración es sumar los bits más pequeños para obtener el área completa bajo la curva.
Integrales definidas
Hay dos formas posibles de integración: integración definida e integración indefinida. La integración definida se realiza para el área dada con límites o fronteras, es decir, la curva es finita y, por lo tanto, el área bajo la curva también será finita, mientras que la integración indefinida se utiliza para la función que no tiene límites superior o inferior, las funciones son de naturaleza infinita y, por lo tanto, los límites superior e inferior para funciones indefinidas son +∞ y -∞.
Integrales definidas de una función f(x) de a a b cuando la función f es continua en el intervalo cerrado [a, b].
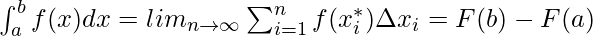
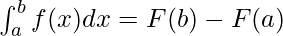
Donde, a y b son los límites inferior y superior.
F(x) es la integral de f(x), y si se deriva f(x), se obtiene F(x). Por lo tanto, se puede decir que F es la antiderivada de f. Las integrales definidas también se conocen como integrales de Riemann.
Evaluación de Integrales Definidas — Propiedades
En Matemáticas, sumas y sumas simples son fáciles, pero cuando se trata de evaluar integrales complejas, los cálculos y sumas simples no son suficientes, por lo tanto, se requiere Integración. Al evaluar integrales definidas, a veces los cálculos se vuelven demasiado engorrosos y complejos, por lo que se realizan algunas propiedades comprobadas empíricamente para que los cálculos sean relativamente fáciles.
Propiedad 1: ![]()
Esta propiedad se puede probar simplemente sustituyendo el valor de «t» en lugar de «x».
Propiedad 2: ![]()
Prueba: Sea F(x) la antiderivada de la integral
.
Entonces, sabemos
Comparando estas dos ecuaciones, podemos deducir que
Por lo tanto, Probado.
Propiedad 3: ![]()
Prueba:
La suma de las dos ecuaciones anteriores nos dará la primera ecuación,
Propiedad 4: ![]()
Prueba: supongamos que t = a + b -x. Entonces dt = -dx, Cuando x = a, t = b y wh
en x = b, t = a.
Por lo tanto,
Propiedad 5: ![]()
Prueba: Esta propiedad es una propiedad de caso particular 4, por lo que también se puede probar de esa manera.
Propiedad 6: ![]()
Prueba: Usando la Propiedad 3, podemos escribir esto como,
Sea t = 2a x en la segunda integral del lado derecho. Entonces dt = – dx. Cuando x = a, t = a y cuando x = 2a, t = 0. Además, x = 2a – t. Por lo tanto, la segunda integral se convierte en
Por eso, \
Propiedad 7: 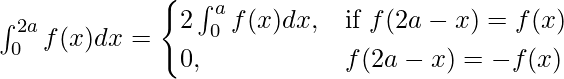
Prueba: Usando la propiedad 6, tenemos
Ahora, si f(2a – x) = f(x) entonces esta ecuación se convierte en,
Y si f(2a – x) = – f (x), entonces esa ecuación se convierte en
Propiedad 8: ![]() si es una función par, es decir, si f(-x) = f(x).
si es una función par, es decir, si f(-x) = f(x).
Propiedad 9: ![]() , si es una función impar, es decir, f(-x) = -f(x).
, si es una función impar, es decir, f(-x) = -f(x).
Prueba: Usando la Propiedad 3, tenemos,
Sea t = – x en la primera integral del lado derecho.
dt = – dx. Cuando x = – a, t = a y cuando x = 0, t = 0. Además, x = – t.
Entonces, podemos reescribir la expresión anterior como,
1. Ahora, si f es una función par, es decir, f(-x) = f(x),
2. Si f es una función impar, es decir, f (–x) = – f(x).
Problemas de muestra
Pregunta 1: Evaluar, ![]()
Solución:
integrando,
Pregunta 2: Evaluar, ![]()
Solución:
Integrando la función dada arriba,
Pregunta 3: Evaluar, ![]()
Solución:
Integrando la función,
Pregunta 4: Dado, ![]() . Encuentre el valor de
. Encuentre el valor de ![]() .
.
Solución:
Para resolver esta pregunta, usaremos la Propiedad 3.
Ahora, solo tenemos que reemplazar el valor de las integrales definidas dadas.
Pregunta 5: Dado f(x) = x 3 . Encuentre el valor de ![]() .
.
Solución:
Ahora bien, esta respuesta se puede calcular a través del método de integración habitual, es bastante fácil. Pero podemos pensar en una propiedad que se puede usar aquí para ahorrar completamente su cálculo y tiempo.
La propiedad 8 y la propiedad 9 se pueden usar según el tipo de función f(x) = x 3 , par o impar. Comprobemos si f(x) es par o impar.
Para una función par, f(-x) = f(x) y para una función impar f(-x) = -f(x).
Aquí en nuestro caso, f(-x) = (-x) 3 = -x 3 = -f(x). Entonces es una función impar.
Por lo tanto, la Propiedad 9 es aplicable aquí, ya través de la propiedad 9 podemos decir eso.
Pregunta 6: Dado, ![]() . Encuentre el valor de
. Encuentre el valor de ![]() .
.
Solución:
Esta pregunta es similar a la que resolvimos hace un momento. También requiere la aplicación de la Propiedad 3. Pero debemos hacer algo al respecto .
Este problema se puede resolver aplicando la Propiedad 2.
Usando la propiedad 2,
Entonces, ahora conectando los valores,
Pregunta 7: Evaluar, 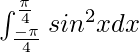
Solución:
En preguntas anteriores, buscamos una función par o impar. Mediante una verificación similar, podemos decir que sen 2 x es una función par.
Entonces, por la propiedad de uso 8, podemos reescribirlo como,
Pregunta 8: Evaluar, ![]()
Solución:
Esta expresión contiene dos términos. Sabemos,
Sin(x) es una función impar y x 4 es una función par.
Asi que,
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

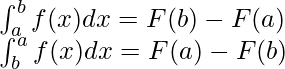
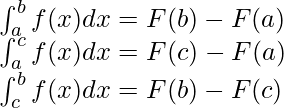


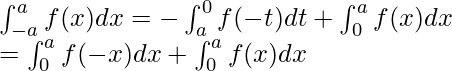
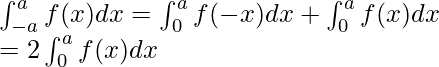

![Rendered by QuickLaTeX.com \int_{1}^{3}x^2dx=[\frac{x^3}{3}]_{1}^{3} \\=1/3[(27)-(1)] \\=26/3 \\=8.66](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7b010d3f12d807361b91b6463e03202f_l3.png)
![Rendered by QuickLaTeX.com \int_{0}^{\pi/2}sinxdx=[cosx]_{0}^{\pi/2} \\=[cos\pi/2-cos0] \\=0-1 \\=-1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-645d3889b3ace776a4bc135b6870dbcc_l3.png)
![Rendered by QuickLaTeX.com \int_{-2}^{1}e^yxdx=e^y[\frac{x^2}{2}] \\e^y[\frac{x^2}{2}]_{-2}^{1} \\\frac{e^y}{2}[1-(-4)] \\\frac{e^y}{2}(5)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b3020b62db201ff3a0987d4d81e3563d_l3.png)
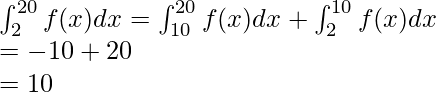
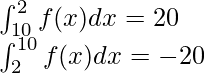
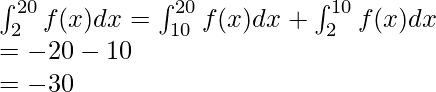
![Rendered by QuickLaTeX.com \int^{\frac{\pi}{4}}_{\frac{-\pi}{4}}sin^2xdx = 2\int^{\frac{\pi}{4}}_{0}sin^2xdx \\ = 2\int^{\frac{\pi}{4}}_{0}\frac{1-cos2x}{2}dx \\ = \int^{\frac{\pi}{4}}_{0}(1-cos2x)dx = [x - \frac{1}{2}sin2x]^{\frac{\pi}{4}}_{0}\\ = \frac{\pi}{4} - \frac{1}{2}sin(\frac{\pi}{2}) = \frac{\pi}{4} - \frac{1}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c368206df6d2d6ac83a8e00f9caec4ca_l3.png)
![Rendered by QuickLaTeX.com \int^{10}_{-10}(x^4 + sinx)dx \\ = \int^{10}_{-10}x^4dx + \int^{10}_{-10}sinxdx \\ = 2\int^{10}_{0}x^4dx + 0 \\ = 2[\frac{x^5}{5}]^{10}_{0} \\ = 2(\frac{100000}{5}) \\ = 40000](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7b0f00317770c1db036d00be86d8b2b9_l3.png)