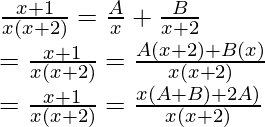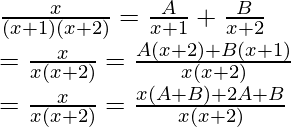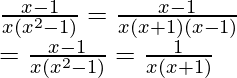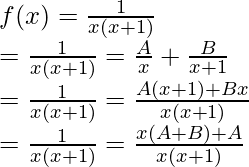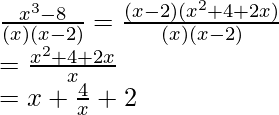Si f(x) es una función que se requiere integrar, f(x) se denomina Integrando, y la integración de la función sin límites ni fronteras se conoce como Integración indefinida. La integración indefinida tiene sus propias fórmulas para facilitar el proceso de integración. Sin embargo, a veces hay funciones que son demasiado complejas y no se pueden integrar fácilmente y requieren más tiempo. Por ejemplo, tener una expresión cuadrática larga en el denominador de la función. En tales casos, la integración indefinida se puede hacer con la ayuda de fracciones parciales para que el proceso sea más fácil y menos lento.
Integración indefinida
Las integraciones indefinidas también se conocen como antiderivadas, ya que es el proceso inverso de la diferenciación. Indefinido significa que la función se integra sin límites ni fronteras y se requiere que se integre toda la función. La función, digamos f(x), es el Integrando, x aquí es la variable de la integración, y el símbolo usado para la integración es ∫. Echemos un vistazo a algunas fórmulas básicas utilizadas para la integración indefinida,
Algunas fórmulas básicas de integración indefinida:
| Funciones | fórmulas |
| ∫a dx | hacha + C, a∈ R |
| ∫x n dx | |
| ∫1/x dx | registro|x| + C |
| ∫e x dx | e x + C |
| ∫1/√x dx | 2√x + C |
| ∫a x dx | |
| ∫Senx dx | -Cosx +C |
| ∫Cosx dx | Sinx +C |
| ∫Tanx dx | log|secx| +C |
| ∫Secx tanx dx | Secx + C |
| ∫Cosecx cotx dx | -Cosecx + C |
| ∫ Seg 2 x dx | tanx +C |
| ∫ Cosec 2 x dx | – cotx + C |
Ejemplo 1: Encuentra la integración de la función,
f(x) = x5 + 3 /x
Solución:
∫f(x)dx = ∫x 5 dx + ∫3/x dx
∫f(x)dx =
Ejemplo 2: Integra, f(x)= 5cosx – 9tanx
Solución:
∫f(x)dx= ∫[5cosx- 9tanx]dx
∫f(x)dx= ∫5cosxdx- ∫9tanxdx
∫f(x)dx= 5senx- (log|secx|) +C
Además de los problemas simples que solo requieren fórmulas, es importante comprender que las funciones complejas no se pueden resolver tan fácilmente. Para encontrar la integración de la función compleja, un método es usar fracciones parciales,
Integración por Fracción Parcial
Las funciones racionales se definen como las funciones que tienen la forma de P(x)/Q(x) donde Q(x) ≠ 0. Estas funciones pueden estar en forma propia o impropia. La función de ración adecuada se define como aquella en la que el mayor grado en Q(x) es mayor que en P(x). Las funciones impropias son aquellas en las que P(x) tiene su mayor grado más que Q(x). Las funciones racionales se pueden integrar por fracción parcial muy fácilmente siempre que el denominador en la función se pueda factorizar en factores lineales.
Descomposición en fracciones parciales
El integrando, es decir, la función dada se puede factorizar en una forma más simple y esto se denomina descomposición en fracciones parciales. A continuación se dan algunas fracciones parciales generalizadas de las funciones,
| Funciones | Fracciones parciales |
|
x 2 + bx+ c no se puede factorizar |
¿Cómo se obtienen estas formas generalizadas o hay pasos que se pueden usar para la descomposición en fracciones parciales? SÍ. Los pasos pueden ayudar fácilmente a alcanzar una forma de fracción parcial perfecta,
Pasos para la descomposición de fracciones parciales
- Para descomponer, comience con la expresión racional adecuada. Factoriza el denominador en la forma más básica.
- Anota las fracciones parciales separadas obtenidas y, para tratar con el numerador, llénalas con variables que se conocerán próximamente.
- Ahora, para encontrar el valor de las variables, aquí, A, B y C, multiplica la ecuación por el denominador.
- Resuelve las variables sustituyendo diferentes valores según corresponda.
- Cuando obtengas los valores de los numeradores, colócalos en la fracción parcial.
Integración mediante División Larga o División Sintética
Este método se utiliza cuando las funciones no están dadas en forma racional, es decir, las fracciones son fracciones impropias y el grado del numerador es mayor o igual que el grado del denominador. En estos casos, suponga que el grado en el numerador es a y el grado en el denominador es b, al hacer fracciones parciales aquí, debe tenerse en cuenta que se agrega un valor adicional de (ab) a los denominadores junto con el fracciones parciales.
Consideremos la función dada a continuación:
f(x) = ![]()
Esta función es una integral impropia, por lo que se puede resolver mediante el método de división larga.

Aquí, S(x) = x 5 – 6x 4 + 5x 2 + 8 y R(x) = -100 y Q(x) = x + 2.
Entonces, la integral se puede reescribir como,
∫(x 5 – 6x 4 + 5x 2 + 8 + ![]() )dx
)dx
⇒ 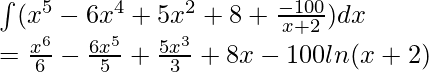
división larga impropia de polinomios
Después de hacer esto, la función se puede integrar.
Problemas de muestra
Pregunta 1: Integra, f(x)= sin(x) + 3tanx
Solución :
∫f(x)dx= ∫[sen(x) + 3tanx]dx
∫f(x)dx= ∫sen(x)dx + ∫3tanxdx
∫f(x)dx= -cos(x) + 3(log|segx|) +C
Pregunta 2: Encuentra la integral de la siguiente función.
f(x) = ![]()
Solución:
La función dada se puede descomponer en fracciones parciales.
f(x) =
Comparando ambos lados de la ecuación,
A + B = 1
2A = 1
De estas dos ecuaciones, se puede concluir que.
A = 1/2, B = 1/2
Así, la función se convierte en,
f(x) =
Ahora,
F(x) = ∫f(x)
⇒ F(x) =
⇒ F(x) =
Pregunta 3: Encuentra la integral de la siguiente función.
f(x) = ![]()
Solución:
La función dada se puede descomponer en fracciones parciales.
f(x) =
Comparando ambos lados de la ecuación,
A + B = 1
2A + B = 0
De estas dos ecuaciones, se puede concluir que.
A = -1, B = 2
Así, la función se convierte en,
f(x) =
Ahora,
F(x) = ∫f(x)
⇒ F(x) =
⇒ F(x) =
Pregunta 4: Encuentra la integral de la siguiente función.
f(x) = ![]()
Solución:
La función dada se puede descomponer en fracciones parciales. Primero simplifiquemos la función.
f(x) =
Descomponiendo la función,
Comparando ambos lados de la ecuación,
A + B = 0
un = 1
De estas dos ecuaciones, se puede concluir que.
A = 1, B = -1
Así, la función se convierte en,
f(x) =
Ahora,
F(x) = ∫f(x)
⇒ F(x) =
⇒ F(x) = ln(x) – ln(x+1)
Pregunta 5: Encuentra la integral de la siguiente función.
f(x) = ![]()
Solución:
La función dada se puede descomponer en fracciones parciales. Primero simplifiquemos la función.
f(x) =
Integrando la función,
F(x) = ∫f(x)dx
⇒ F(x) = ∫(
)dx
⇒ F(x) =
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA