En un partido de cricket, antes de que comience el juego. Dos capitanes van por un sorteo. Lanzar es una actividad de lanzar una moneda y comprobar el resultado como «cara» o «cruz». De manera similar, lanzar un dado nos da un número del 1 al 6. Todas estas actividades son ejemplos de experimentos. Una actividad que nos da un resultado se llama experimento. Puede haber más de un resultado de un experimento. El campo de la probabilidad está más relacionado con los experimentos aleatorios. Estos experimentos no tienen un resultado definitivo, es decir, no se puede predecir el resultado de estos experimentos con absoluta certeza.
Experimentos
La teoría de la probabilidad se basa en experimentos. Un experimento es una prueba, ensayo o procedimiento con el propósito de descubrir algo desconocido, probar un principio o suposición, etc. A continuación, se enumeran algunas actividades que pueden considerarse experimentos:
- Lance la moneda repetidamente y anote los resultados. Hay dos resultados posibles: cara (H) o cruz (T).
- Tirar un dado justo y observar el número que da como resultado.
- Conduciendo de Delhi a Bangalore y midiendo la distancia entre las dos ciudades.
Todas las actividades enumeradas anteriormente pueden describirse como experimentos. Observe que en la actividad 1 y la actividad 2 no sabemos el resultado de la actividad y no podemos decir con certeza qué número aparecerá en el dado o si saldremos cara o cruz con el lanzamiento de la moneda. El resultado de la actividad 3 se puede predecir fácilmente. Esto significa que hay aleatoriedad involucrada en el experimento 1 y 2. Estos experimentos se denominan experimentos aleatorios.
Experimentos aleatorios
La suposición subyacente de la teoría de la probabilidad es que los experimentos deben ser aleatorios. Se supone que el experimento se puede realizar infinitas veces en las mismas condiciones. Esta suposición se vuelve importante porque tanto la teoría de la probabilidad clásica como la teoría de la probabilidad basada en la frecuencia se basan en esta suposición al buscar los comportamientos a largo plazo en los experimentos.
Un experimento aleatorio se define como un experimento cuyo resultado no se puede predecir con certeza.
Es imposible predecir el resultado cuando se lanza un dado. Este es un ejemplo de un experimento aleatorio. Cada experimento aleatorio debe cumplir las dos condiciones siguientes:
- El experimento se puede repetir varias veces en las mismas condiciones.
- El resultado del experimento no se puede predecir de antemano con certeza.
Para ilustrar este concepto, tomemos este experimento como ejemplo.
Se lanza una moneda dos veces y se registran los resultados. Los posibles resultados son:
HH, HT, JU, TT
La siguiente figura representa los resultados en forma de árbol.
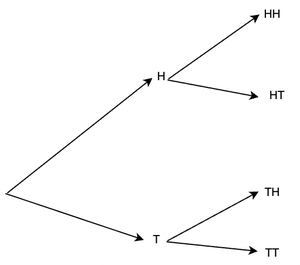
Observe que hay cuatro resultados posibles en este experimento y ninguno de ellos se puede predecir de antemano. El conjunto de todos los resultados posibles constituye el espacio muestral del experimento aleatorio. Así, en el contexto de nuestro experimento, el espacio muestral es un conjunto universal. Se denota como S. Para el experimento anterior,
S = {HT, HH, TH, TT}
Cuando un experimento se repite varias veces, cada una de ellas se denomina ensayo . Por lo tanto, un ensayo puede describirse como una ejecución particular de un experimento aleatorio. En este experimento en particular, una prueba es el lanzamiento de la moneda. Dos de estos ensayos constituyen el experimento completo.
Eventos y probabilidades
Para un experimento con el espacio muestral S, el objetivo es asignar probabilidades a ciertos resultados. Para entender el concepto de eventos, consideremos un experimento nuevamente. Se lanzan dos dados, estamos interesados en los resultados donde la suma de los números de dados es igual a 6. El primer paso es considerar el espacio muestral para este experimento.
S = {(1,1); (1,2); …..(dieciséis);
(2,1); (2,2); … (2,6);
(3,1); (3,2); ….(3,6);
(4,1); (4,2); …..(4,6);
(5,1); (5,2); ……(5,6);
(6,1); (6,2); ……(6,6); }
Estos son todos los resultados posibles de este experimento.
Un evento es el subconjunto del espacio muestral.
En este caso, el evento serán los resultados donde la suma del número en los dados es igual a 6. Contendrá todos aquellos resultados del conjunto S, donde la suma de los números es 6. Digamos que el evento se denota adiós,
E = {(2,4); (4,2); (3,3); (3,3); (1,5); (5,1)}
La cardinalidad de este conjunto |E| = 6 mientras que la cardinalidad del espacio muestral |S| = 36.
La probabilidad se define como la relación entre el número favorable de resultados y el número total de resultados posibles.
P(Evento) =
Para este caso,
P(E) = ![]()
⇒ P(E) = ![]()
⇒ P(E) = ![]()
⇒ P(E) = ![]()
Veamos algunos ejemplos sobre estos conceptos.
Problemas de muestra
Pregunta 1: Escribe el espacio muestral para tres lanzamientos de una moneda.
Responder:
Un lanzamiento de moneda da Cara (H) o Cruz (T).
El resultado de tres lanzamientos de monedas será triples de cara y cruz.
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
Pregunta 2: De las siguientes actividades dadas a continuación. Elige actividades aleatorias:
- Sacar una bola de una urna que contiene bolas blancas y negras.
- Multiplicando 4 y 8 en la calculadora.
- nacimiento de una persona
Responder:
Cada experimento/actividad aleatoria debe cumplir las siguientes dos condiciones:
- El experimento se puede repetir varias veces en las mismas condiciones.
- El resultado del experimento no se puede predecir de antemano con certeza.
Sacar una bola de una urna que contiene bolas blancas y negras.
Esto se puede repetir tantas veces como sea necesario, y tampoco se puede predecir qué bola se extraerá. Por lo tanto, es una actividad aleatoria.
Multiplicando 4 y 8 en la calculadora.
Esta actividad se puede repetir varias veces, pero el resultado de esta actividad se puede predecir de antemano. Por lo tanto, no es una actividad aleatoria.
nacimiento de una persona
No se puede repetir el nacimiento de una persona. Por lo tanto, no es una actividad aleatoria.
Pregunta 3: Considere un experimento de tirar un dado y luego lanzar una moneda. Dibujar el espacio muestral.
Responder:
Cuando se lanza un dado, se obtiene {1, 2, 3, 4, 5, 6} como resultado, mientras que al lanzar una moneda se obtiene {H, T}.
Espacio muestral S = {(1, H); (2, H); (3, H); (4,H); (5,H); (6,H); (1, T); (2, T); (3, T); (4, T); (5, T); (6, V)}
Pregunta 4: Calcula la probabilidad de obtener 2 caras en tres lanzamientos de una moneda.
Responder:
Un lanzamiento de moneda da Cara (H) o Cruz (T).
El resultado de tres lanzamientos de monedas será triples de cara y cruz. Entonces, el espacio muestral es,
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
Contando el número de resultados favorables, hay tres resultados con dos caras.
probabilidad =
PAG =
Pregunta 5: Encuentra la probabilidad de sacar un as de una baraja de cartas bien barajada.
Responder:
Una baraja de cartas contiene 52 cartas y de las cuales 4 son ases. La fórmula de la probabilidad,
probabilidad =
Número favorable de resultados = 4
Número total de resultados = 52
probabilidad =
⇒ P =
⇒ P =
Pregunta 6: Calcula la probabilidad de obtener al menos 1 cara en tres lanzamientos de una moneda.
Responder:
Un lanzamiento de moneda da Cara (H) o Cruz (T).
El resultado de tres lanzamientos de monedas será triples de cara y cruz. Entonces, el espacio muestral es,
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
Contando el número de resultados favorables, hay siete resultados con al menos una cara.
probabilidad =
PAG =
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

