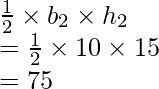Figuras sobre la misma base y entre los mismos paralelos

Un triángulo es un polígono de tres lados y un paralelogramo es un polígono de cuatro lados o simplemente un cuadrilátero que tiene lados opuestos paralelos. Encontramos estos dos polinomios en casi todas partes en nuestra vida cotidiana. Por ejemplo: Digamos que un agricultor tiene un terreno que tiene la forma de un paralelogramo. Quiere dividir esta tierra en dos partes para sus hijas. Ahora, cuando se divide en dos partes, generará dos triángulos. Por lo que, en este caso, se vuelve fundamental para nosotros conocer sus zonas. Las fórmulas simples para calcular las áreas de triángulos y paralelogramos a veces pueden ser engorrosas. Entonces, usamos algunos teoremas y propiedades para simplificar nuestros cálculos en tales escenarios. Veamos estas propiedades en detalle. 

paralelogramos y triangulos 

Los triángulos tienen tres lados y los paralelogramos son los cuadriláteros que tienen cuatro lados mientras que los lados opuestos son paralelos entre sí. La siguiente figura muestra un paralelogramo y un triángulo. Digamos que «b2» y «h2» son la longitud de la base y la altura del triángulo respectivamente y «b1» y «h1» son la base y la altura del paralelogramo. 

 

Área del triángulo = 

Área del paralelogramo = 

Figuras congruentes y sus áreas

Sabemos que dos figuras se llaman congruentes si tienen el mismo tamaño y forma. Entonces, si dos figuras son congruentes, puedes superponerlas y ambas cubrirán completamente a la otra figura. Eso significa que si dos figuras cualesquiera son congruentes, sus áreas deben ser iguales. Pero fíjate que el recíproco de esta afirmación no es cierto, si dos figuras tienen áreas iguales, no es necesario que ambas sean congruentes. En la siguiente figura, podemos ver dos pares de figuras que son congruentes y tienen las mismas áreas, pero el otro par de figuras tienen las mismas áreas, pero no son congruentes. 

En la figura anterior, comparemos las áreas de dos cuadriláteros. 

Ar(PQRS) = 9 × 4 = 36 

Ar(TUVW) = 6 ² = 36

Observe que ambos tienen la misma área, pero no son congruentes. Esto verifica que lo contrario de nuestra declaración que dimos antes no es cierto. Entonces, ahora la definición del área se puede resumir de la siguiente manera, 

El área de una figura es la medida del plano que está encerrado por esa figura. Tiene las siguientes dos propiedades: 

1. Digamos que tenemos dos figuras X e Y. Si X e Y son figuras congruentes, entonces ar(X) = ar(Y).
2. Si ambas figuras se combinan sin superponerse para formar otra figura T. El área de la figura T vendrá dada por, ar(T) = ar(X) + ar(Y).

Paralelogramos sobre la misma base y entre los mismos paralelos

Nuestro objetivo es aprender sobre la relación entre las áreas de dos paralelogramos cuando tienen la misma base y están entre los mismos paralelos. La siguiente figura muestra dos paralelogramos con una base común y entre las mismas líneas paralelas. Probemos la relación entre estas áreas con algunos teoremas. 

Teorema: Los paralelogramos con la misma base y entre los mismos paralelos tienen la misma área.

Prueba: 

Supongamos que tenemos dos paralelogramos PQRS y RSTU como se muestra en la siguiente figura. Ambos tienen la misma base RS y están entre los mismos paralelos. El objetivo es probar que ar(PQRS) = ar(RSTU). 

En la figura, RSTQ es común a ambos paralelogramos. Ahora, si podemos probar que ar(PST) = ar(QRU). Podemos probar que las áreas de ambos paralelogramos son iguales. 

Veamos el triángulo PST y QRU. 

∠SPT = ∠RQU (Ángulos correspondientes) 

∠PTS = ∠QUR (Ángulos correspondientes)

Ahora, dado que dos ángulos de triángulos son iguales, el tercer ángulo también será igual debido a la propiedad de la suma de ángulos. 

∠PST = ∠QRU 

Ahora ambos triángulos son congruentes 

ΔPST≅ ΔQRU

Así, ar(PST) = ar(QRU) 

Ahora sabemos que, 

Ar(PQRS) = ar(RSTQ) + ar(PST) 

Ar(RSTU) = ar(RSTQ) + ar(QRU) 

Dado que ar(RSTQ) es común y ar(PST) = ar(QRU). 

Así, ar(PQRS) = ar(RSTU)

Triángulos sobre la misma base y entre los mismos paralelos

La siguiente figura representa dos triángulos que están en la misma base y están entre los mismos paralelos. Nuestro objetivo es encontrar la relación entre las áreas de estos dos triángulos. Veamos teoremas relacionados con 

Teorema: Dos triángulos sobre la misma base y entre los mismos paralelos tienen igual área. 

Prueba:

Sabemos que el área del triángulo está dada por 

Entonces, dos triángulos tendrán la misma área si tienen la misma base y altura. 

Nuestros triángulos tienen una base común. Ahora bien, como están entre dos paralelos, deben tener la misma altura. Por lo tanto, ambos triángulos tienen la misma área. 

Ejemplos de preguntas

Pregunta 1: Encuentra el área del triángulo y el paralelogramo dados en las siguientes figuras. 

Solución: 

Sabemos, 

Área del triángulo = 

Área del paralelogramo = b ₂ × h ₂

= 3 × 5 

= 15

Pregunta 2: Indique tres propiedades de un paralelogramo. 

Responder: 

Tres propiedades del paralelogramo: 

1. Los lados opuestos son paralelos e iguales.
2. Los ángulos opuestos son iguales.
3. Los ángulos adyacentes suman 180°.

Pregunta 3: En el triángulo ΔPQR de la siguiente figura, PS es la mediana. Demuestre que ar(PSR) = ar(PQS). 

Responder: 

Ahora si dibujamos una perpendicular desde el vértice P a la base QR. Veremos que esta perpendicular es común a los dos del triángulo. Por lo tanto, ambos tienen la misma base y la misma altura. Por lo tanto, deben tener la misma área. 

Pregunta 4: En la siguiente figura, tenemos un rectángulo RSTU y un paralelogramo PQRS. Se da que, PL es perpendicular a RS. Ahora, prueba:

1. Ar(RSTU) = ar(PQRS) 
2. Ar(PQRS) = RS x AL.  

Solución: 

1. Sabemos que los rectángulos también son paralelogramos. Entonces, el teorema que estudiamos también se aplica al rectángulo. Ambas figuras tienen la misma base y se encuentran entre los mismos paralelos. Por lo tanto, ambos deben tener la misma área. 

Ar(RSTU) = ar(PQRS) 

2. El área del paralelogramo = base x altura. 

Ar(PQRS) = RU x RS

Como PURL también es un rectángulo, RU = AL. De este modo, 

Ar(PQRS) = RS x AL. 

Pregunta 5: Un agricultor tiene un campo que tiene la forma de un paralelogramo PQRS. El agricultor toma un punto en RS y lo une a P, Q. Responda las siguientes preguntas: 

1. ¿Cuántas porciones tiene ahora en el campo ? 
2. Quiere sembrar maíz y caña de azúcar, qué porciones debe usar para que ambos se cultiven en la misma área. 

Solución: 

1. Deje que el punto que el agricultor elija sea X. Una X con P y Q. Esto divide el campo en tres partes. 

2. Ahora, sabemos que si un triángulo y un paralelogramo tienen la misma base y están entre los mismos paralelos. Entonces, el área del triángulo es la mitad del área del paralelogramo. 

Entonces, en este caso, ar(XPQ) = 1/2(ar(PQRS) 

Entonces, las dos porciones restantes deben formar la otra mitad del área. Eso significa,

Ar(XPQ) = ar(XPS) + ar(XQR) 

Por lo tanto, debería cultivar un cultivo en XPQ y otro cultivo tanto en XPS como en XQR.