Los filtros Bloom son para la pertenencia a un conjunto que determina si un elemento está presente en un conjunto o no. El filtro Bloom fue inventado por Burton H. Bloom en 1970 en un artículo llamado Space/Time Trade-offs in Hash Coding with Allowable Errors (1970) . El filtro Bloom es una estructura de datos probabilística que funciona con métodos de codificación hash (similar a HashTable ).
¿Cuándo necesitamos un filtro Bloom?
Considere cualquiera de las siguientes situaciones:
- Supongamos que tenemos una lista de algunos elementos y queremos verificar si un elemento dado está presente o no.
- Considere que está trabajando en un servicio de correo electrónico y está tratando de implementar un punto final de registro con una función que indica que un nombre de usuario dado ya está presente o no.
- Suponga que ha proporcionado un conjunto de IP en la lista negra y desea filtrar una IP dada si está en la lista negra o no.
¿Se pueden resolver estos problemas sin la ayuda de Bloom Filter?
Intentemos resolver estos problemas usando un HashSet
import java.util.HashSet;
import java.util.Set;
public class SetDemo {
public static void main(String[] args)
{
Set<String> blackListedIPs
= new HashSet<>();
blackListedIPs.add("192.170.0.1");
blackListedIPs.add("75.245.10.1");
blackListedIPs.add("10.125.22.20");
// true
System.out.println(
blackListedIPs
.contains(
"75.245.10.1"));
// false
System.out.println(
blackListedIPs
.contains(
"101.125.20.22"));
}
}
true false
¿Por qué falla la estructura de datos como HashSet o HashTable ?
HashSet o HashTable funcionan bien cuando tenemos un conjunto de datos limitado, pero es posible que no encajen a medida que avanzamos con un conjunto de datos grande. Con un gran conjunto de datos, lleva mucho tiempo con mucha memoria.
Tamaño del conjunto de datos frente al tiempo de inserción para HashSet como estructura de datos
---------------------------------------------- |Number of UUIDs Insertion Time(ms) | ---------------------------------------------- |10 <1 | |100 3 | |1, 000 58 | |10, 000 122 | |100, 000 836 | |1, 000, 000 7395 | ----------------------------------------------
Tamaño del conjunto de datos frente a la memoria (JVM Heap) para una estructura de datos similar a HashSet
---------------------------------------------- |Number of UUIDs JVM heap used(MB) | ---------------------------------------------- |10 <2 | |100 <2 | |1, 000 3 | |10, 000 9 | |100, 000 37 | |1, 000, 000 264 | -----------------------------------------------
Entonces, está claro que si tenemos un gran conjunto de datos, entonces una estructura de datos normal como Set o HashTable no es factible, y aquí los filtros Bloom entran en escena. Consulte este artículo para obtener más detalles sobre la comparación entre los dos: Diferencia entre los filtros Bloom y Hashtable
¿Cómo resolver estos problemas con la ayuda de Bloom Filter?
Tomemos una array de bits de tamaño N (aquí 24) e inicialicemos cada bit con cero binario. Ahora tomemos algunas funciones hash (puede tomar tantas como desee, estamos tomando dos funciones hash aquí para nuestra ilustración).
- Ahora pase la primera IP que tiene a ambas funciones hash, lo que genera un número aleatorio como se indica a continuación
hashFunction_1(192.170.0.1) : 2 hashFunction_2(192.170.0.1) : 6
Ahora, vaya al índice 2 y 6 y marque el bit como binario 1.
- Ahora pasa la segunda IP que tienes, y sigue el mismo paso.
hashFunction_1(75.245.10.1) : 4 hashFunction_2(75.245.10.1) : 10
Ahora, vaya al índice 4 y 10 y marque el bit como binario 1.
- De manera similar, pase la tercera IP a ambas funciones hash, y suponga que obtuvo el siguiente resultado de la función hash
hashFunction_1(10.125.22.20) : 10 hashFunction_2(10.125.22.20) : 19
‘
Ahora, vaya al índice 10 y 19 y márquelo como binario 1. Aquí el índice 10 ya está marcado por la entrada anterior, así que simplemente marque el índice 19 como binario 1. - Entrada de prueba #1
Digamos que queremos verificar IP 75.245.10.1 . Pase esta IP con las mismas dos funciones hash que hemos tomado para agregar las entradas anteriores.hashFunction_1(75.245.10.1) : 4 hashFunction_2(75.245.10.1) : 10
Ahora, vaya al índice y verifique el bit, si tanto el índice 4 como el 10 están marcados con un 1 binario, entonces la IP 75.245.10.1 está presente en el conjunto; de lo contrario, no está en el conjunto de datos.
- Entrada de prueba #2
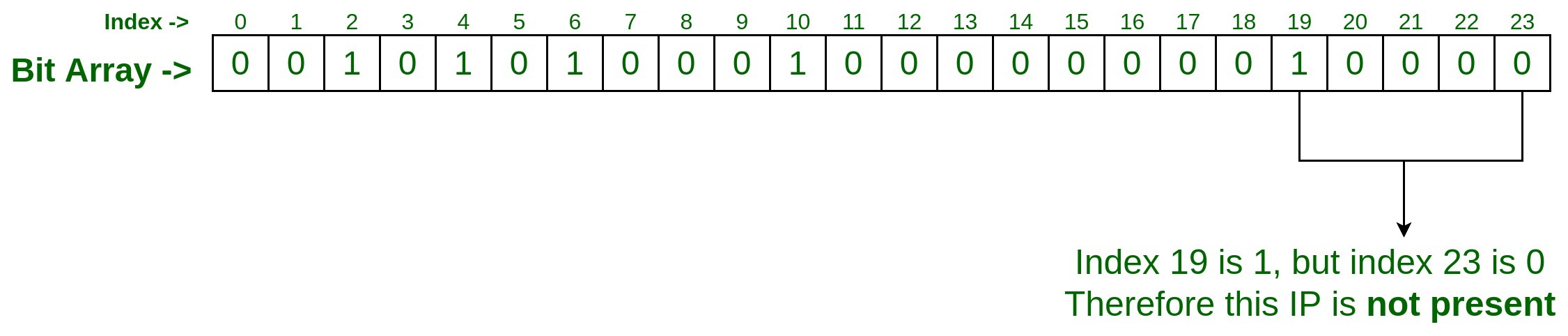
Digamos que queremos verificar si IP 75.245.20.30 está presente en el conjunto o no. Entonces, el proceso será el mismo, pase esta IP con las mismas dos funciones hash que hemos tomado para agregar las entradas anteriores.hashFunction_1(75.245.20.30) : 19 hashFunction_2(75.245.20.30) : 23
Dado que en el índice 19 está establecido en 1, pero en el índice 23 es 0, podemos decir que la IP 75.245.20.30 dada no está presente en el conjunto.
Ahora, es hora de verificar si una IP está presente en el conjunto de datos o no.
¿Por qué Bloom Filter es una estructura de datos probabilística?
Entendamos esto con una prueba más, esta vez considere una IP 101.125.20.22 y verifique si está presente en el conjunto o no. Pase esto a ambas funciones hash. Considere los resultados de nuestra función hash de la siguiente manera.
hashFunction_1(101.125.20.22) : 19 hashFunction_2(101.125.20.22) : 2
Ahora, visite el índice 19 y 2 que está configurado en 1 y dice que la IP 101.125.20.22 dada está presente en el conjunto.
Pero esta IP 101.125.20.22 se procesó anteriormente en el conjunto de datos mientras se agregaban las IP a la array de bits. Esto se conoce como falso positivo :
Expected Output: No Actual Output: Yes (False Positive)
En este caso, los índices 2 y 19 se establecieron en 1 por otra entrada y no por esta IP 101.125.20.22 . A esto se le llama colisión y por eso es probabilístico , donde las posibilidades de que suceda no son del 100%.
¿Qué esperar de un filtro Bloom?
- Cuando un filtro Bloom dice que un elemento no está presente , es seguro que no está presente . Garantiza al 100% que el elemento dado no está disponible en el conjunto, porque cualquiera de los bits de índice proporcionados por las funciones hash se establecerán en 0.
- Pero cuando el filtro Bloom dice que el elemento dado está presente , no es 100% seguro , porque puede haber una posibilidad debido a la colisión, todo el bit de índice dado por las funciones hash se ha establecido en 1 por otras entradas.
¿Cómo obtener un resultado 100% preciso de un filtro Bloom?
Bueno, esto solo podría lograrse tomando más funciones hash. Cuanto mayor sea el número de la función hash que tomemos, más preciso será el resultado que obtendremos, debido a las menores posibilidades de colisión.
Complejidad de tiempo y espacio de un filtro Bloom
Supongamos que tenemos alrededor de 40 millones de conjuntos de datos y estamos usando alrededor de funciones hash H , entonces:
Complejidad temporal: O(H) , donde H es el número de funciones hash utilizadas
Complejidad espacial: 159 Mb (para 40 millones de conjuntos de datos)
Caso de falso positivo: 1 error por 10 millones (para H = 23)
Implementación del filtro Bloom en Java usando la biblioteca Guava:
podemos implementar el filtro Bloom usando la biblioteca Java proporcionada por Guava .
- Incluya la siguiente dependencia maven:
<dependency><groupId>com.google.guava</groupId><artifactId>guava</artifactId><version>19.0</version></dependency> - Escriba el siguiente código para implementar el filtro Bloom:
// Java program to implement// Bloom Filter using Guava Libraryimportjava.nio.charset.Charset;importcom.google.common.hash.BloomFilter;importcom.google.common.hash.Funnels;publicclassBloomFilterDemo {publicstaticvoidmain(String[] args){// Create a Bloom Filter instanceBloomFilter<String> blackListedIps= BloomFilter.create(Funnels.stringFunnel(Charset.forName("UTF-8")),10000);// Add the data setsblackListedIps.put("192.170.0.1");blackListedIps.put("75.245.10.1");blackListedIps.put("10.125.22.20");// Test the bloom filterSystem.out.println(blackListedIps.mightContain("75.245.10.1"));System.out.println(blackListedIps.mightContain("101.125.20.22"));}}Producción:
Nota: El código Java anterior puede devolver un 3 % de probabilidad de falso positivo de forma predeterminada.
- Reducir la probabilidad de falso positivo
Introducir otro parámetro en la creación del objeto de filtro Bloom de la siguiente manera:
BloomFilterblackListedIps = BloomFilter.create(Funnels.stringFunnel(Charset.forName("UTF-8")), 10000, 0.005); Ahora la probabilidad de falso positivo se ha reducido de 0,03 a 0,005 . Pero ajustar este parámetro tiene un efecto en el lado del filtro de floración.
Efecto de reducir la probabilidad de falso positivo:
analicemos este efecto con respecto a la función hash, el bit de array, la complejidad del tiempo y la complejidad del espacio.
- Veamos el tiempo de inserción para diferentes conjuntos de datos.
----------------------------------------------------------------------------- |Number of UUIDs | Set Insertion Time(ms) | Bloom Filter Insertion Time(ms) | ----------------------------------------------------------------------------- |10 <1 71 | |100 3 17 | |1, 000 58 84 | |10, 000 122 272 | |100, 000 836 556 | |1, 000, 000 7395 5173 | ------------------------------------------------------------------------------
- Ahora, echemos un vistazo a la memoria (montón JVM)
-------------------------------------------------------------------------- |Number of UUIDs | Set JVM heap used(MB) | Bloom filter JVM heap used(MB) | -------------------------------------------------------------------------- |10 <2 0.01 | |100 <2 0.01 | |1, 000 3 0.01 | |10, 000 9 0.02 | |100, 000 37 0.1 | |1, 000, 000 264 0.9 | ---------------------------------------------------------------------------
- recuentos de bits
---------------------------------------------- |Suggested size of Bloom Filter | Bit count | ---------------------------------------------- |10 40 | |100 378 | |1, 000 3654 | |10, 000 36231 | |100, 000 361992 | |1, 000, 000 3619846 | -----------------------------------------------
- Número de funciones hash utilizadas para varias probabilidades de falso positivo:
----------------------------------------------- |Suggested FPP of Bloom Filter | Hash Functions| ----------------------------------------------- |3% 5 | |1% 7 | |0.1% 10 | |0.01% 13 | |0.001% 17 | |0.0001% 20 | ------------------------------------------------
Conclusión:
Por lo tanto, se puede decir que el filtro Bloom es una buena opción en una situación en la que tenemos que procesar grandes conjuntos de datos con un bajo consumo de memoria. Además, cuanto más preciso sea el resultado que queremos, se debe aumentar la cantidad de funciones hash.
Publicación traducida automáticamente
Artículo escrito por asadaliasad y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA