Dado un número n, encuentre las firmas primos ordenadas y, usando esto, encuentre el número de divisor de n dado.
Cualquier número entero positivo, ‘n’ se puede expresar en forma de sus factores primos. Si ‘n’ tiene p 1 , p 2 , … etc. como sus factores primos, entonces n se puede expresar como: ![]()
Ahora, ordene los exponentes obtenidos de los factores primos de ‘n’ en orden no decreciente. La disposición así obtenida se llama firma prima ordenada del entero positivo ‘n’.
Ejemplo:
Input : n = 20
Output :
The Ordered Prime Signature of 20 is :
{ 1, 2 }
The total number of divisors of 20 is 6
Input : n = 13
Output :
The Ordered Prime Signature of 13 is :
{ 1 }
The total number of divisors of 13 is 2
Explicación :
 firma prima ordenada de 20 = { 1, 2 }
firma prima ordenada de 20 = { 1, 2 }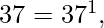 firma prima ordenada de 37 = { 1 }
firma prima ordenada de 37 = { 1 }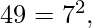 firma prima ordenada de 49 = { 2 }
firma prima ordenada de 49 = { 2 }
Se puede determinar a partir de la discusión anterior que la firma principal de 1 es { 1 }. Además, todos los números primos tienen la misma firma, es decir, {1} y la firma prima de un número, que es la k-ésima potencia de un número primo (por ejemplo, 25, que es la 2-a potencia de 5), siempre es {k}.
Por ejemplo :
Primera firma ordenada de 100 = { 2, 2 }, como 100 = 2 ^ 2 × 5 ^ 2
Ahora, agregar uno a cada elemento da { 3, 3 } y el producto es 3 × 3 = 9,
es decir, el número total de divisores de 100 es nueve.
Son 1, 2, 4, 5, 10, 20, 25, 50, 100.
Enfoque:
1) Encuentra la descomposición en factores primos del número
2) Almacena cada exponente correspondiente a un factor primo, en un vector
3) Ordena el vector en orden ascendente
4) Agrega uno a cada elemento presente en el vector
5) Multiplica todos los elementos
C++
// CPP to find total number of divisors of a
// number, using ordered prime signature
#include <bits/stdc++.h>
using namespace std;
// Finding primes upto entered number
vector<int> primes(int n)
{
bool prime[n + 1];
// Finding primes by Sieve
// of Eratosthenes method
memset(prime, true, sizeof(prime));
for (int i = 2; i * i <= n; i++)
{
// If prime[i] is not changed,
// then it is prime
if (prime[i] == true) {
// Update all multiples of p
for (int j = i * 2; j <= n; j += i)
prime[j] = false;
}
}
vector<int> arr;
// Forming array of the prime numbers found
for (int i = 2; i <= n; i++)
{
if (prime[i])
arr.push_back(i);
}
return arr;
}
// Finding ordered prime signature of the number
vector<int> signature( int n)
{
vector<int> r = primes(n);
// Map to store prime factors and
// the related exponents
map<int, int> factor;
// Declaring an iterator for map
map<int, int>::iterator it;
vector<int> sort_exp;
int k, t = n;
it = factor.begin();
// Finding prime factorization of the number
for (int i = 0; i < r.size(); i++)
{
if (n % r[i] == 0) {
k = 0;
while (n % r[i] == 0) {
n = n / r[i];
k++;
}
// Storing the prime factor and
// its exponent in map
factor.insert(it, pair<int, int>(r[i], k));
// Storing the exponent in a vector
sort_exp.push_back(k);
}
}
// Sorting the stored exponents
sort(sort_exp.begin(), sort_exp.end());
// Printing the prime signature
cout << " The Ordered Prime Signature of " <<
t << " is : \n{ ";
for (int i = 0; i < sort_exp.size(); i++)
{
if (i != sort_exp.size() - 1)
cout << sort_exp[i] << ", ";
else
cout << sort_exp[i] << " }\n";
}
return sort_exp;
}
// Finding total number of divisors of the number
void divisors(int n)
{
int f = 1, l;
vector<int> div = signature(n);
l = div.size();
// Adding one to each element present
for (int i = 0; i < l; i++)
{
// in ordered prime signature
div[i] += 1;
// Multiplying the elements
f *= div[i];
}
cout << "The total number of divisors of " <<
n << " is " << f << "\n";
}
// Driver Method
int main()
{
int n = 13;
divisors(n);
return 0;
}
Java
// JAVA to find total number of divisors of a
// number, using ordered prime signature
import java.util.*;
class GFG
{
static class pair
{
int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
// Finding primes upto entered number
static Vector<Integer> primes(int n)
{
boolean []prime = new boolean[n + 1];
// Finding primes by Sieve
// of Eratosthenes method
Arrays.fill(prime, true);
for (int i = 2; i * i <= n; i++)
{
// If prime[i] is not changed,
// then it is prime
if (prime[i] == true) {
// Update all multiples of p
for (int j = i * 2; j <= n; j += i)
prime[j] = false;
}
}
Vector<Integer> arr = new Vector<>();
// Forming array of the prime numbers found
for (int i = 2; i <= n; i++)
{
if (prime[i])
arr.add(i);
}
return arr;
}
// Finding ordered prime signature of the number
static Vector<Integer> signature( int n)
{
Vector<Integer> r = primes(n);
// Map to store prime factors and
// the related exponents
HashMap<Integer,Integer> factor = new HashMap<>();
// Declaring an iterator for map
// HashMap<Integer,Integer>::iterator it;
Vector<Integer> sort_exp = new Vector<>();
int k, t = n;
int it = 0;
// Finding prime factorization of the number
for (int i = 0; i < r.size(); i++)
{
if (n % r.get(i) == 0)
{
k = 0;
while (n % r.get(i) == 0)
{
n = n / r.get(i);
k++;
}
// Storing the prime factor and
// its exponent in map
factor.put(r.get(i), k);
// Storing the exponent in a vector
sort_exp.add(k);
}
}
// Sorting the stored exponents
Collections.sort(sort_exp);
// Printing the prime signature
System.out.print(" The Ordered Prime Signature of " +
t+ " is : \n{ ");
for (int i = 0; i < sort_exp.size(); i++)
{
if (i != sort_exp.size() - 1)
System.out.print(sort_exp.get(i) + ", ");
else
System.out.print(sort_exp.get(i) + " }\n");
}
return sort_exp;
}
// Finding total number of divisors of the number
static void divisors(int n)
{
int f = 1, l;
Vector<Integer> div = signature(n);
l = div.size();
// Adding one to each element present
for (int i = 0; i < l; i++)
{
// in ordered prime signature
//div[i] += 1;
// Multiplying the elements
f *= (div.get(i) + 1);
}
System.out.print("The total number of divisors of " +
n + " is " + f + "\n");
}
// Driver code
public static void main(String[] args)
{
int n = 13;
divisors(n);
}
}
// This code is contributed by aashish1995
C#
// C# to find total number
// of divisors of a number,
// using ordered prime signature
using System;
using System.Collections.Generic;
class GFG
{
// Finding primes
// upto entered number
static List<int> primes(int n)
{
bool []prime = new bool[n + 1];
// Finding primes by Sieve
// of Eratosthenes method
for (int i = 0; i < n + 1; i++)
prime[i] = true;
for (int i = 2; i * i <= n; i++)
{
// If prime[i] is not
// changed, then it is prime
if (prime[i] == true)
{
// Update all multiples of p
for (int j = i * 2;
j <= n; j += i)
prime[j] = false;
}
}
List<int> arr = new List<int>();
// Forming array of the
// prime numbers found
for (int i = 2; i <= n; i++)
{
if (prime[i])
arr.Add(i);
}
return arr;
}
// Finding ordered prime
// signature of the number
static List<int> signature( int n)
{
List<int> r = primes(n);
// Map to store prime factors
// and the related exponents
var factor = new Dictionary<int, int>();
List<int> sort_exp = new List<int>();
int k, t = n;
// Finding prime factorization
// of the number
for (int i = 0; i < r.Count; i++)
{
if (n % r[i] == 0)
{
k = 0;
while (n % r[i] == 0)
{
n = n / r[i];
k++;
}
// Storing the prime factor
// and its exponent in map
factor.Add(r[i], k);
// Storing the exponent
// in a List
sort_exp.Add(k);
}
}
// Sorting the
// stored exponents
sort_exp.Sort();
// Printing the
// prime signature
Console.Write(" The Ordered Prime Signature of " +
t + " is : \n{ ");
for (int i = 0; i < sort_exp.Count; i++)
{
if (i != sort_exp.Count - 1)
Console.Write(sort_exp[i] + ", ");
else
Console.Write(sort_exp[i] + " }\n");
}
return sort_exp;
}
// Finding total number
// of divisors of the number
static void divisors(int n)
{
int f = 1, l;
List<int> div = signature(n);
l = div.Count;
// Adding one to each
// element present
for (int i = 0; i < l; i++)
{
// in ordered
// prime signature
div[i] += 1;
// Multiplying
// the elements
f *= div[i];
}
Console.Write("The total number of divisors of " +
n + " is " + f + "\n");
}
// Driver Code
static void Main()
{
int n = 13;
divisors(n);
}
}
// This code is contributed by
// Manish Shaw(manishshaw1)
Javascript
<script>
// JavaScript to find total number of divisors of a
// number, using ordered prime signature
// Finding primes upto entered number
function primes(n)
{
// Finding primes by Sieve
// of Eratosthenes method
let prime = new Array(n+1).fill(true);
for (let i = 2; i * i <= n; i++)
{
// If prime[i] is not changed,
// then it is prime
if (prime[i] == true) {
// Update all multiples of p
for (let j = i * 2; j <= n; j += i)
prime[j] = false;
}
}
let arr = new Array();
// Forming array of the prime numbers found
for (let i = 2; i <= n; i++)
{
if (prime[i])
arr.push(i);
}
return arr;
}
// Finding ordered prime signature of the number
function signature(n)
{
let r = primes(n);
// Map to store prime factors and
// the related exponents
let factor = new Map();
let sort_exp = new Array();
let k;
let t = n;
// Finding prime factorization of the number
for (let i = 0; i < r.length; i++)
{
if (n % r[i] == 0) {
k = 0;
while (n % r[i] == 0) {
n = Math.floor(n / r[i]);
k = k + 1;
}
// Storing the prime factor and
// its exponent in map
factor.set(r[i], k);
// Storing the exponent in a vector
sort_exp.push(k);
}
}
// Sorting the stored exponents
sort_exp.sort();
// Printing the prime signature
document.write(" The Ordered Prime Signature of ", t, " is :\n");
document.write("{");
for (let i = 0; i < sort_exp.length; i++)
{
if (i != sort_exp.length - 1)
document.write(sort_exp[i],",");
else
document.write(sort_exp[i], " } \n");
}
return sort_exp;
}
// Finding total number of divisors of the number
function divisors(n)
{
let f = 1;
let l;
let div = signature(n);
l = div.length;
// Adding one to each element present
for (let i = 0; i < l; i++)
{
// in ordered prime signature
div[i] += 1;
// Multiplying the elements
f *= div[i];
}
document.write("The total number of divisors of ", n, " is ", f);
}
// Driver Method
let n = 13;
divisors(n);
// This code is contributed by gautamgoel962.
</script>
The Ordered Prime Signature of 13 is :
{ 1 }
The total number of divisors of 13 is 2
Aplicación:
encontrar la firma prima ordenada de un número tiene utilidades para encontrar el número de divisores. De hecho, el número total de divisores de un número puede deducirse de la firma ordenada de primos de ese número. Para lograr esto, simplemente agregue uno a cada elemento presente en la firma principal ordenada y luego multiplique esos elementos. El producto así obtenido da el número total de divisores del número (incluyendo el 1 y el propio número).
Publicación traducida automáticamente
Artículo escrito por SaagnikAdhikary y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA