Formas de eliminar bordes de un gráfico completo para hacer bordes impares

Dado un grafo completo con N vértices, la tarea es contar el número de formas de eliminar aristas de modo que el grafo resultante tenga un número impar de aristas.
Ejemplos: 
 

Entrada: N = 3 
Salida: 4 
El gráfico inicial tiene 3 aristas ya que es un gráfico completo. Podemos quitar los bordes (1, 2) y (1, 3) o (1, 2) y (2, 3) o (1, 3) y (2, 3) o no quitar ninguno de los bordes.
Entrada: N = 4 
Salida: 32 
 

Enfoque: Como el gráfico está completo, el número total de aristas será E = N * (N – 1) / 2 . Ahora hay dos casos, 
 

1. Si E es par , debe eliminar el número impar de aristas, por lo que el número total de formas será 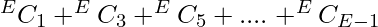 equivalente a  .
2. Si E es impar , entonces debe eliminar el número par de aristas, por lo que el número total de formas será 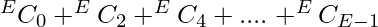 equivalente a  .

Tenga en cuenta que si N = 1 , la respuesta será 0 .
A continuación se muestra la implementación del enfoque anterior: 
 

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to return the number of ways
// to remove edges from the graph so that
// odd number of edges are left in the graph
int countWays(int N)
{
    // Total number of edges
    int E = (N * (N - 1)) / 2;
 
    if (N == 1)
        return 0;
 
    return pow(2, E - 1);
}
 
// Driver code
int main()
{
    int N = 4;
    cout << countWays(N);
 
    return 0;
}

// Java implementation of the approach
class GfG
{
 
// Function to return the number of ways
// to remove edges from the graph so that
// odd number of edges are left in the graph
static int countWays(int N)
{
    // Total number of edges
    int E = (N * (N - 1)) / 2;
 
    if (N == 1)
        return 0;
 
    return (int)Math.pow(2, E - 1);
}
 
// Driver code
public static void main(String[] args)
{
    int N = 4;
    System.out.println(countWays(N));
}
}
 
// This code is contributed by Prerna Saini

# Python3 implementation of the approach
 
# Function to return the number of ways
# to remove edges from the graph so that
# odd number of edges are left in the graph
def countWays(N):
     
    # Total number of edges
    E = (N * (N - 1)) / 2
 
    if (N == 1):
        return 0
 
    return int(pow(2, E - 1))
 
# Driver code
if __name__ == '__main__':
    N = 4
    print(countWays(N))
 
# This code contributed by PrinciRaj1992

// C# implementation of the approach
 
using System;
 
public class GFG{
     
// Function to return the number of ways
// to remove edges from the graph so that
// odd number of edges are left in the graph
static int countWays(int N)
{
    // Total number of edges
    int E = (N * (N - 1)) / 2;
 
    if (N == 1)
        return 0;
 
    return (int)Math.Pow(2, E - 1);
}
 
// Driver code
    static public void Main (){
     
    int N = 4;
    Console.WriteLine(countWays(N));
    }
}
// This code is contributed by ajit.

<?php
// PHP implementation of the approach
 
// Function to return the number of ways
// to remove edges from the graph so that
// odd number of edges are left in the graph
function countWays($N)
{
    // Total number of edges
    $E = ($N * ($N - 1)) / 2;
 
    if ($N == 1)
        return 0;
 
    return (int)pow(2, $E - 1);
}
 
// Driver code
$N = 4;
echo(countWays($N));
 
// This code is contributed
// by Code_Mech.
?>

<script>
    // Javascript implementation of the approach
     
    // Function to return the number of ways
    // to remove edges from the graph so that
    // odd number of edges are left in the graph
    function countWays(N)
    {
        // Total number of edges
        let E = parseInt((N * (N - 1)) / 2, 10);
 
        if (N == 1)
            return 0;
 
        return Math.pow(2, E - 1);
    }
     
    let N = 4;
    document.write(countWays(N));
 
</script>

32

Complejidad temporal: O(log E), donde E = (N * (N – 1)) / 2.

Espacio Auxiliar: O(1)