Hay varios tipos de triángulos entre ellos algunos se dice que son especiales, 30-60-90 están entre ellos. Normalmente nos referimos a un triángulo como rectángulo si uno de los ángulos es de 90°. Por lo tanto, podemos decir que 30-60-90 es un tipo especial de triángulo rectángulo. Este tipo de triángulo siempre tendrá sus ángulos de 30°, 60° y 90°.
Fórmula 30-60-90
La siguiente figura representa el triángulo 30-60-90 con ∠A = 60°, ∠B = 90° y ∠C = 30°. El 30-60-90 se pronuncia como “treinta – sesenta – noventa”.

30-60-90 Triángulo
El lado que representa opuesto al ángulo 30° tiene el valor más pequeño y sea “a” cm. Otro lado que representa opuesto al ángulo 60° tiene el valor moderado y es “a√3” cm. Por último, el lado que representa opuesto al ángulo de 90° tiene el mayor valor y es “2a” cm.
De la siguiente figura,
- AB = a cm (Opuesto al ángulo 30°) ⇢ Lado más corto
- BC = a√3 cm (Opuesto al ángulo 60°) ⇢ Lado intermedio
- AC = 2a cm (Opuesto al ángulo 90°) ⇢ Lado mayor
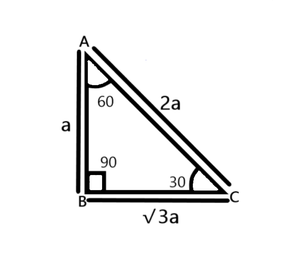
Por lo tanto, AB:BC:CA = a:√3a:2a
Negando “a” ya que es común. Ahora, mire la razón de los lados del triángulo 30-60-90, es decir, 1:√3:2.
Para probar esto, consideremos un triángulo equilátero, es decir, el triángulo en el que todos los lados tienen la misma longitud, y sea «a» cm.

Consideremos primero el triángulo equilátero (todos los lados son iguales y forman un ángulo de 60° en los vértices) como se muestra en la figura. Si trazamos una línea desde uno de los vértices (digamos A) hasta el otro lado (digamos BC). Luego, el otro lado, es decir, BC, se divide en 2 mitades iguales (cada parte con a/2) y forma un ángulo de 90°. Sea D el punto divisorio o el punto medio de BC. Debido a la línea que se dibuja, el ángulo en el vértice A que es de 60° también se dividirá por igual y cada parte tiene 30°.
Ahora mira la mitad de la figura que es el triángulo ABD, se asemeja a un triángulo 30-60-90 con lados AB = a cm, BD = a/2 cm, AD = desconocido (digamos x cm)
Para encontrar el valor de AD usemos el teorema de Pitágoras, que establece que “En un triángulo rectángulo, el cuadrado del lado de la hipotenusa (lado más largo) es igual a la suma de los cuadrados de los otros dos lados”, de la figura AB es la hipotenusa, BD y AD son otros 2 lados.
Por lo tanto,
AB 2 = BD 2 + AD 2
un 2 = (a/2) 2 + x 2
x2 = un 2 – (un/2 ) 2
x = √3a/2 cm (AD)
La razón de los lados opuestos a los ángulos 30-60-90 será a/2: √3a/2: a ⇒ 1:√3:2 (tomando como común y despreciando y multiplicando por 2)
Esta relación 1:√3:2 se conoce como fórmula 30-60-90
Área del Triángulo 30-60-90
Para encontrar el área de 30-60-90, consideremos la fórmula común para el área del triángulo, es decir, = 1/2 × base × altura
Para el triángulo, ABD, AD actúan como altura (√3a/2 cm), y BD actúan como base (a/2)
Por lo tanto el área del triángulo =1/2 × a/2 × √3a/2
Área = √3a 2 /8
Problemas de muestra
Pregunta 1: Si los 2 de los lados del triángulo 30-60-90 miden 20 cm y 40 cm, encuentra el otro lado.
Solución:
Dados 2 lados son 20 y 40, que están en la razón de 1:2
Para encontrar el tercer lado, es decir, x de la fórmula 30-60-90 1:√3:2 x ⇒ √3a
x ⇒ 20 × √3 cm.
x = 20√3cm
Pregunta 2: El lado más corto del 30-60-90 mide 40 cm, encuentra el área del triángulo?
Solución:
Dado que el lado más corto mide 40 cm, es decir, a = 40 cm.
El área de 30-60-90 se da como (√3 × a 2 )/8
Por lo tanto Área ⇒ (√3 × 40 × 40) / 8
⇒ 200√3 cm 2 .
Pregunta 3: El lado más largo del 30-60-90 mide 120 cm, encuentra el área del triángulo?
Solución:
Dado que el lado más largo mide 120 cm, es decir, 2a = 120 cm.
Por lo tanto, a = 60 cm.
El área de 30-60-90 se da como (√3 × a 2 )/8
Por lo tanto Área ⇒ (√3 × 60 × 60) / 8
⇒ 450√3 cm 2 .
Pregunta 4: El lado moderado del 30-60-90 es 12√3cm, encuentra el área del triángulo?
Solución:
Dado que el lado moderado mide 120 cm, es decir, a√3 = 12√3 cm.
Por lo tanto, a = 12 cm.
El área de 30-60-90 se da como (√3 × a 2 )/8
Por lo tanto Área ⇒ (√3 × 12 × 12) / 8
⇒ 18√3 cm 2 .
Pregunta 5: El lado más corto del triángulo mide 90 cm, ¿cuál es el lado más largo?
Solución:
Dado que el lado más corto de 30-60-90 es 90 cm.
De la fórmula 30-60-90 los lados más cortos y más largos están en la razón 1:2 ⇒ x:2x
Dado x = 90 2x = ?
Por tanto, 2x = 2 × 90 = 180 cm.
Pregunta 6: El lado más largo del triángulo mide 20 cm, ¿cuál es la longitud del lado intermedio?
Solución:
Dado que el lado más largo de 30-60-90 mide 20 cm.
De la fórmula 30-60-90 los lados mayor e intermedio están en la razón 2:√3 ⇒ 2x :√3 x
Dado 2x = 20
X = 10
Por lo tanto, √3x = √3 × 10 = 10√3 cm.
Publicación traducida automáticamente
Artículo escrito por kandimallaommahalakshmi y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
