Fórmula de cálculo integral

El cálculo es una parte importante de las matemáticas. El cálculo integral es la rama de las matemáticas que se ocupa de la teoría y las aplicaciones de las integrales. Las antiderivadas de una función se llaman integrales de la función. Este artículo trata sobre varias fórmulas de cálculo integral y sus problemas. Las fórmulas integrales básicas se utilizan en varias otras fórmulas.

Cálculo integral

El cálculo integral es una rama del cálculo que se ocupa de la teoría y las aplicaciones de las integrales. El proceso de encontrar integrales se llama integración. El cálculo integral ayuda a encontrar las antiderivadas de una función. Las antiderivadas también se llaman integrales de una función. Se denota por ∫ f(x)dx. El cálculo integral se ocupa del valor total, como longitudes, áreas y volúmenes. La integral se puede usar para encontrar soluciones aproximadas a ciertas ecuaciones de datos dados. El cálculo integral implica dos tipos de integración: integrales indefinidas y definidas.

Fórmula de cálculo integral

Las diversas fórmulas de cálculo integral son

$\frac{d}{dx}$ {φ(x)} = f(x) <=> ∫f(x) dx = φ(x) + C
∫ X norte ^dx = 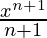$\frac{x^{n+1}}{n+1}$ + C, norte ≠ -1
∫(1/x) dx = log _e |x| + C
∫e ^x dx = e ^x + C
∫a ^x dx = (a ^x / log _e a) + C
∫sen x dx = – cos x + C
∫cos x dx = sen x + C
∫seg ² x dx = tan x + C
∫coseg ² x dx = -cot x + C
∫sec x tan x dx = sec x + C
∫cosec x cot x dx = – cosec x + C
∫cot x dx = log |sin x| + C
∫tan x dx = – log |cos x| + C
∫sec x dx = log |sec x + tan x| + C
∫cosec x dx = log |cosec x – cot x| + C
$\int\frac{1}{\sqrt{a^2 -x^2}}$ dx = sen ^-1 (x/a) + C
$\int-\frac{1}{\sqrt{a^2 -x^2}}$ dx = cos ^-1 (x/a) + C
$\int\frac{1}{{a^2 + x^2}}$ dx = (1/a)tan ^-1 (x/a) + C
$\int-\frac{1}{{a^2 +x^2}}$ dx = (1/a)cot ^-1 (x/a) + C
$\int\frac{1}{x\sqrt{x^2-a^2}}$ dx = (1/a)seg ^-1 (x/a) + C
$\int-\frac{1}{x\sqrt{x^2-a^2}}$ dx = (1/a)coseg ^-1 (x/a) + C

Nota:

$\frac{d}{dx}(\int f(x) dx)$ = f(x)

∫k. f(x) dx = k ∫f(x) dx , donde k es constante

∫{f(x) ± g(x)} dx = ∫f(x) dx ± ∫g(x) dx

Problemas de muestra

Pregunta 1: Evaluar

(i)∫ x ⁶ dx (ii) ∫1/x ⁴ dx (iii) ∫ ³ √x dx (iv)∫3 ^x dx (v) ∫4e ^x dx (vi) ∫(sen x/cos ² x) dx (vii) ∫(1/sen ² x) dx (viii) ∫[1/√(4 – x ² )] dx (ix) ∫[1/3√(x ² – 9)] dx (x) ∫ (1 /cos x tan x) dx

Solución:

(i)∫x ⁶ dx = (x ⁶⁺¹ )/(6 + 1) + C [∫x ⁿ dx = {x ⁿ⁺¹ /(n+1)} + C n ≠ -1]

= (x ⁷ /7) + C

(ii) ∫1/x ⁴ dx = ∫x ^-4 dx [∫x ⁿ dx = {x ⁿ⁺¹ /(n+1)} + C n ≠ -1]

= (x ^-4+1 )/(-4 + 1) + C

= -(x ^-3 / 3) + C

= -(1/3x ³ ) + C

(iii) ∫ ³ √x dx = ∫x ^1/3 dx    [∫x ⁿ dx = {x ⁿ⁺¹ /(n+1)}+ C n ≠ -1]

= (x ^(1/3)+1 /((1/3)+ 1) + C

= x ^4/3 / (4/3) + C

= (3/4)(x ^4/3 ) + C

(iv) ∫3 ^x dx = (3 ^x / log _e 3) + C    [ ∫a ^x dx = (a ^x / log _e a) + C]

(v) ∫4e ^x dx = 4∫e ^x dx [∫k . f(x) dx = k f(x) dx , donde k es constante]

= 4 e ^x + C    [∫e ^x dx = e ^x + C]

(vi) ∫(sen x/cos ² x) dx = ∫[(sen x/cos x) .(1/cos x)] dx

= ∫ bronceado x . sec x dx    [ ∫tan x .sec x dx = sec x + C ]

= segundo x + C

(vii) ∫(1/sen ² x) dx = ∫cosec ² x dx [∫cosec ² x dx = -cot x + C ]

= -cuna x + C

(viii) ∫[1/√(4 – x ² )] dx = ∫[1/√(2 ² – x ² )] dx [ $\int\frac{1}{\sqrt{a^2 -x^2}}$ dx = sen ^-1 (x/a) + C]

= sen ^-1 (x/2) + C

(ix) ∫[1/{3√(x ² – 9)}] dx = ∫[1/{3√(x ² – 3 ² )}] dx [ $\int\frac{1}{x\sqrt{x^2-a^2}}$ dx = (1/a)seg ^-1 (x /a) + C]

= (1/3)seg ^-1 (x/3) + C

(x) ∫(1 /cos x tan x) dx = ∫[cos x /(cos x sen x)] dx

= ∫(1/ sen x) dx

= ∫cosec x dx [∫cosec x dx = log |cosec x – cot x| + C]

= log |cosec x – cot x| + C

Pregunta 2: Evalúa ∫{e ^9log_^e^x + e ^8log_^e^x }/{e ^6log_^e^x + e ^5log_^e^x } dx

Solución:

Ya que, e ^alog_^e^x = x ^a

∫{e ^9log_^e^x + e ^8log_^e^x }/{e ^6log_^e^x + e ^5log_^e^x } dx = ∫{x ⁹ + x ⁸ }/{x ⁶ + x ⁵ } dx

= ∫[x ⁸ (x + 1)]/[x ⁵ (x + 1)] dx

=∫ x ⁸ /x ⁵ dx

= ∫x ³ dx [∫x norte ^dx = {x norte ⁺¹ /(n+1)} + C norte ≠ -1]

= (x ⁴ /4) + C

Pregunta 3: Evalúa ∫ sen x + cos x dx

Solución:

∫(sen x + cos x) dx = ∫sen x dx + ∫cos x dx [∫{f(x) ± g(x)} dx = ∫f(x) dx ± ∫g(x) dx]

= -cos x + sen x + C [∫ sen x dx = -cos x + C , ∫ cos x dx = sen x + C ]

Pregunta 4: Evalúa ∫4 ^x+2 dx

Solución:

∫4 ^x+2 dx = ∫4 ^x . 4 ² dias

= ∫16. 4 ^x dx [∫kf(x) dx = k∫f(x) dx , donde k es constante]

= 16∫ 4 ^x dx [∫a ^x dx = (a ^x / log _e a) + C]

= 16 (4 ^x /log 4) + C

Pregunta 5: Evalúa ∫(x ² + 3x + 1) dx

Solución:

∫(x ² + 3x + 1) dx = ∫x ² dx+ 3∫x dx + 1∫ x ⁰ dx [∫x ⁿ dx = {x ⁿ⁺¹ /(n+1)}+ C n ≠ -1]

= [x ²⁺¹ /2+1] + 3[[x ¹⁺¹ /1+1]] + [x ⁰⁺¹ /0+1] + C

= [x ³ /3] + 3[x ² /2] + x + C

Pregunta 6: Evalúa ∫[4/(1 + cos 2x)] dx

Solución:

Ya que, 1 + cos 2x = 2 cos ² x

∫[4/(1 + cos 2x)] dx = ∫[4/( ² cos 2x) ] dx

= ∫(2/cos ² x) dx

= ∫2 sec ² xdx [∫kf(x) dx = k ∫f(x) dx , donde k es constante]

= 2∫seg ² x dx [∫seg ² x dx = tan x + C ]

= 2 tan x + C

Pregunta 7: Evalúa ∫(3cos x – 4sen x + 5 sec ² x) dx

Solución:

∫(3cos x – 4sen x + 5 seg ² x) dx = ∫3cos x dx – ∫4sen x dx + ∫5sec ² x dx [∫kf(x) dx = k ∫f(x) dx, donde k es constante ]

= 3∫cos x dx – 4∫sen x dx + 5∫seg ² x dx

[∫cos x dx = sen x + C , ∫sen x dx = -cos x + C , ∫sec ² x dx = tan x +C ]

= 3sen x – 4(-cos x) + 5 tan x + C

= 3sen x + 4cos x + 5 tan x + C

Publicación traducida automáticamente

Artículo escrito por aayushi2402 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Cálculo integral

Fórmula de cálculo integral

Problemas de muestra

Deja una respuesta Cancelar la respuesta