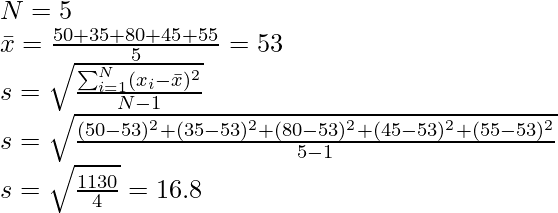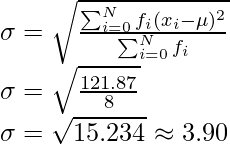En estadística, la medida de la variación de los valores se conoce como Desviación Estándar (DE). Un valor bajo de SD implica que el conjunto de valores dado se extiende sobre un rango pequeño, mientras que un valor alto de SD significa que el conjunto de valores se extiende sobre un rango grande. SD a menudo se representa con el alfabeto griego sigma σ para la desviación estándar de la población o con la letra s para la desviación estándar de la muestra. Ahora veremos cuál es la diferencia entre población y muestra y la diferencia entre sus desviaciones estándar. La población se define como todo el grupo sobre el que desea estudiar. Por ejemplo, todos los jugadores de fútbol del Liverpool FC, todos los países del mundo y todos los teléfonos inteligentes del mundo. Una muestra se define como un subgrupo de una población bajo una condición específica. Por ejemplo, todos los delanteros del Liverpool FC,
Población Vs Muestra

Nota: El tamaño de la muestra suele ser menor que el tamaño de la población, pero en algunos casos excepcionales puede ser el mismo. Ahora que conocemos la diferencia entre población y muestra, veamos sus desviaciones estándar.
Fórmula de desviación estándar de la población
σ =
Aquí σ = Desviación estándar de la población
x i = i -ésima observación
μ = media de N observación
N = número de observaciones.
Si x i tiene diferentes probabilidades usamos la fórmula,
Donde p i = probabilidad de x i
Las fórmulas anteriores se utilizan cuando el valor de x es finito. Si nos dan un rango continuo de x , usamos lo siguiente,
Aquí p(x) = función de densidad de probabilidad
E(x) = valor medio o esperado
Desviación estándar de la muestra
La fórmula para la SD de la muestra es muy similar a la SD de la población con cambios menores,
Aquí
= media de la muestra
N = número de muestra
¿De dónde viene la N-1?
Los valores de la muestra estarán naturalmente más cerca de la media muestral ![]() que de la media poblacional μ. Por lo tanto, para compensar esto, de modo que la SD no se subestime, usamos N – 1 en lugar de N en el denominador. Si desea leer más al respecto, siéntase libre de buscar en Google Estimación imparcial de la desviación estándar. Le dará la razón por la que usamos N – 1 y no N – 2, etc.
que de la media poblacional μ. Por lo tanto, para compensar esto, de modo que la SD no se subestime, usamos N – 1 en lugar de N en el denominador. Si desea leer más al respecto, siéntase libre de buscar en Google Estimación imparcial de la desviación estándar. Le dará la razón por la que usamos N – 1 y no N – 2, etc.
Desviación estándar de datos agrupados
Ahora veremos qué hacer si le han dado datos agrupados junto con su frecuencia de aparición. En la distribución de frecuencia discreta, un valor de X corresponde a una frecuencia. Quedará claro a partir de los problemas de muestra a continuación,
Problemas de muestra
Problema 1: encuentre la desviación estándar de X = {2, 2, 3, 4, 6, 7}.
Solución:
norte = 6
X = {2, 2, 3, 4, 6, 7}
m =
= (2 + 2 + 3 + 4 + 6 + 7)/ 6
= 4
= (2 – 4) 2 + (2 – 4) 2 + (3 – 4) 2 + (4 – 4) 2 + (6 – 4) 2 + (7 – 4) 2
= 22
σ = √(22/6)
= 1.914
Problema 2: encuentre la desviación estándar de X = {0, 1, 2, 3, 4} donde la probabilidad de cada valor está dada por p(x) = {0.1, 0.3, 0.1, 0.2, 0.3}.
Solución:
X
p(X)
(A)
X × p(X)
( Xi – μ) 2
(B)
A×B
0
0.1
0
5.29
0.529
1
0.3
0.3
1.69
0.507
2
0.1
0.2
0.09
0.009
3
0.2
0.6
0.49
0.098
4
0.3
1.2
2.89
0.867
Total
2.3
2.01
μ = ∑ pag(x) × x
= 2,3
Problema 3: Encuentre la desviación estándar de X si el pdf de X está dado por la función p(x) = (1 – x) para x ∈ [0, 1].
Solución:
Problema 4: Había 30 estudiantes en la clase. El peso de 5 es el siguiente: 50 kg, 35 kg, 80 kg, 45 kg y 55 kg. Encuentre la desviación estándar de la muestra.
Solución:
Problema 5: encuentre la SD de muestra de los siguientes datos: {5, 6, 10, 12, 13}
Solución:
Problema 6: encuentre la desviación estándar de los siguientes datos,
|
X yo |
yo _ |
|
5 |
2 |
|
12 |
4 |
|
15 |
3 |
Solución:
X yo yo _ X i × f i X i -μ (Xi-μ) 2 f×(Xi-μ)2 5 2 10 -6.375 40.64 81.28 12 3 36 0,625 0.39 1.17 15 3 45 3.625 13.14 39.42 Total 8 91 121.87
Problema 7: encuentre la desviación estándar de la siguiente tabla de datos
| Clase | F |
| 0-10 | 3 |
| 10-20 | 6 |
| 20-30 | 4 |
| 30-40 | 2 |
| 40-50 | 1 |
Solución:
Clase
punto medio
Xi
F
f×xi
Xi-μ
(Xi – μ)2
f×(Xi – μ)2
0-10
5
3
15
-15
225
675
10-20
15
6
90
-5
25
150
20-30
25
4
100
5
25
100
30-40
35
2
70
15
225
450
40-50
45
1
45
25
625
625
Total
dieciséis
320
2000
Publicación traducida automáticamente
Artículo escrito por sohamsinghal32 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
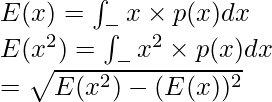
![Rendered by QuickLaTeX.com p(x) = 1-x\\ x\in[0,1]\\ E(x) = \int_{-\infin}^{\infin}x× p(x) = \int_{0}^{1}x×(1-x)dx = [\frac{x^2}{2}-\frac{x^3}{3}]_{0}^{1} = \frac{1}{6}\\ E(x^2) = \int_{-\infin}^{\infin}x^2×p(x) = \int_{0}^{1}x^2×(1-x)dx = [\frac{x^3}{3}-\frac{x^4}{4}]_{0}^{1} = \frac{1}{12}\\ \sigma = \sqrt{E(x^2) - (E(x))^2}\\ \sigma = \sqrt{\frac{1}{12}-\frac{1}{36}}\\ \sigma = \sqrt{0.055} \approx 0.24](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-05e58e585639cf2c202f36c2bfa04566_l3.png)