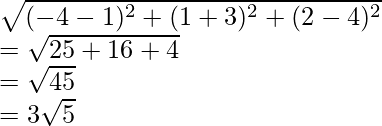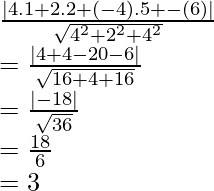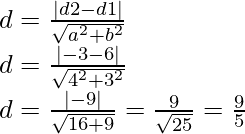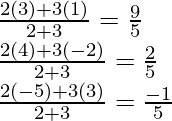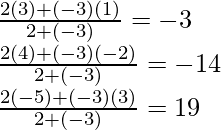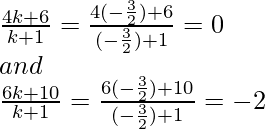Fórmula de distancia y fórmula de sección: geometría tridimensional

Posted on by Rudeus Greyrat

Una de las herramientas más poderosas en el conjunto de herramientas de cualquier ingeniero o científico es la geometría 3D . La geometría 3D llega a la imagen en el modelo de cantidades del mundo real, como la velocidad, los flujos de fluidos, las señales eléctricas y muchas otras cantidades físicas. En este artículo, vamos a discutir dos fórmulas importantes Distancia y Sección junto con algunos ejemplos importantes. Uno puede entender cualquier espacio 3D en términos de 3 coordenadas: x, y y z. A continuación se muestra una representación simple del espacio 3D. 

Representation of Three-dimensional Geometry

Fórmula de distancia y su uso en geometría 3D 

La fórmula de la distancia establece la distancia entre dos puntos en el espacio XYZ. 

Fórmula: 

Para dos puntos P1(x 1 , y 1, z 1 ) y P2(x 2 , y 2, z 2 )

Distancia (d) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}

Esta fórmula de distancia se utiliza para calcular la distancia entre dos puntos en cualquier espacio 3D. Cuando conocemos las coordenadas de los dos puntos en el plano (en forma de par ordenado (x, y, z)) podemos obtener fácilmente la distancia entre dos puntos sustituyendo en la fórmula de la distancia.

La distancia entre dos puntos: fórmulas y ejemplos resueltos 

Suponga que hay dos puntos P(x 1 , y 1, z 1 ) y Q(x 2 , y 2, z 2 ) en el espacio 3D. Para encontrar la distancia entre ellos, la fórmula es,

Distancia (d) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}

Ejemplo 1: ¿Encuentra la distancia entre los puntos P(1, –3, 4) y Q (– 4, 1, 2)?

Solución:

Usando la fórmula para calcular la distancia entre el punto P y Q, 

Distancia (d) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}

re = \sqrt{(-4-1)^2+(1+3)^2+(2-4)^2} \\ =\sqrt{25+16+4} \\ =\sqrt{45} \\ =3 \sqrt{5}

Ejemplo 2: Mostrar que los puntos P (–2, 3, 5), Q (1, 2, 3) y R (7, 0, –1) son colineales.

Solución:

Sabemos que se dice que los puntos son colineales si están sobre una recta.

PQ = \sqrt{(1+2)^2+(2-3)^2+(3-5)^2} = \sqrt{9+1+4} = \sqrt{14}\\ QR = \sqrt{(7-1)^2+(0-2)^2+(-1-3)^2} = \sqrt{36+4+16} =2 \sqrt{14}\\ PR = \sqrt{(7+2)^2+(0-3)^2+(-1-5)^2} = \sqrt{81+9+36} =3 \sqrt{14}  

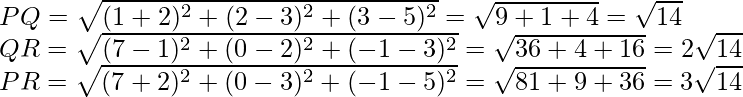
Por tanto, P, Q y R son colineales.

La distancia de un punto a una línea: significado, fórmulas y ejemplos 

La distancia de un punto a una recta es la distancia perpendicular del punto a la recta. Supongamos que tenemos que encontrar la distancia de un punto P(x 0 , y 0, z 0 ) desde la línea l, entonces la fórmula es,

Distancia (d) = \frac{ |\overline{P0P1}* \overline{s}| }{ |\overline{s}| }

Donde ‘s’ es el vector director de la línea l.

Ejemplo: encontrar la distancia desde el punto P (-6, 1, 21) a una línea  \frac{x+4}{3}=\frac{y+5}{1}=\frac{z+1}{1}?

Solución:

L: \frac{(x+4)}3 = \frac{(y+5)}1 = \frac{(z+1)}1 = t \\ P(-6,1,21)\\ P'(3t-4,t-5,t-1) \\ \overline{PP'} = \begin{vmatrix}{3t-4-(-6)} \\ {t-5-1} \\ {t-1-21}\end{vmatrix} = \begin{vmatrix}{3t+2} \\ {t-6} \\ {t-22}\end{vmatrix} \\ \overline{PP'}* \overline{s} = 0 \\ \begin{vmatrix}{3t+2} \\ {t-6} \\ {t-22}\end{vmatrix} . \begin{vmatrix}{3} \\ {1} \\ {1}\end{vmatrix} = 0\\ 9t+6+t-6+t-22=0 \\ 11t-22=0 \\ t=2 \\ \overline{PP'} = \begin{vmatrix}{3(2)+2} \\ {(2)-6} \\ {(2)-22}\end{vmatrix} = \begin{vmatrix}{8} \\ {-4} \\ {-20}\end{vmatrix} = 4\begin{vmatrix}{2} \\ {-1} \\ {-5}\end{vmatrix} \\ d = |\overline{PP'}| = 4 \sqrt{4+1+25} = 4 \sqrt{30}

La distancia de un punto a un plano: fórmulas, ecuaciones y ejemplos

La distancia de un punto a un plano es la distancia perpendicular a un punto del plano. Si Qx + Ry + Sz + T = 0 es una ecuación plana, entonces la distancia desde el punto P(Px, Py, Pz) al plano se puede encontrar usando la siguiente fórmula:

Distancia (d) = \frac{ |Q.P_x+R.P_y+S.P_z+T| }{ \sqrt{Q^2+R^2+S^2} }

Ejemplo: ¿Para encontrar una distancia entre el plano 2x + 4y – 4z – 6 = 0 y el punto P(0, 3, 6)?

Solución: 

Usando la fórmula: 

Distancia (d) = \frac{ |4.1+2.2+(-4).5+-(6)| }{ \sqrt{4^2+2^2+4^2} }\\ =\frac{ |4+4-20-6| }{ \sqrt{16+4+16} }\\ =\frac{ |-18| }{ \sqrt{36} }\\ =\frac{ 18 }{6}\\ =3

La distancia entre rectas paralelas: fórmulas y ejemplos 

La distancia entre dos rectas paralelas es la distancia perpendicular desde cualquier punto de una recta a la otra recta. Supongamos que hay dos rectas paralelas y = mx + c 1 y y = mx + c 2 , entonces la fórmula es,

Distancia (d) = \frac{|c_2-c_1|}{ \sqrt{1+m^2} }

Si la ecuación de dos rectas paralelas se da como:

ax + by + d1 = 0 y ax + by + d2 = 0, entonces la fórmula es,

Distancia (d) = \frac{|d_2-d_1|}{ \sqrt{a^2+b^2} }

Donde a y b son los coeficientes de las variables x e y en la recta.

Ejemplo 1: ¿Encontrar la distancia entre las líneas y = 2x + 10 y y = 2x + 12? (Nota: ambas líneas son paralelas entre sí)

Solución: 

Las rectas y = 2x + 10 e y = 2x + 12 están en la forma y = mx + c.

Dónde 

Usando la fórmula, la distancia (d) =  \frac{|12-10|}{ \sqrt{1+2^2} } = \frac{2}{\sqrt{5}}

Ejemplo 2: Encuentra la distancia entre dos líneas paralelas 4x + 3y + 6 = 0 y 4x + 3y – 3 = 0?

Solución:

Las rectas dadas son 4x + 3y + 6 = 0 y 4x + 3y – 3 = 0. Ambas rectas tienen la forma ax + by + d = 0.

Por eso, 

Usando la fórmula para este caso, la distancia (d) se calculará como:

d = \frac{|d2-d1|}{ \sqrt{a^2+b^2} } \\ d = \frac{|-3-6|}{ \sqrt{4^2+3^2} } \\ d = \frac{|-9|}{ \sqrt{16+9} } = \frac{9}{ \sqrt{25} } = \frac{9}{5}

Fórmula de sección: definición, fórmula vectorial, caso y ejemplos 

La fórmula de sección es el concepto que también se puede implementar en espacios 2D y 3D. En el sistema de tres dimensiones, tenemos que elegir un sistema de coordenadas. Suponga que se dan dos puntos P(x1, y1, z1) y Q (x2, y2, z2) y permita que el punto R (x, y, z) divida internamente a PQ en la razón dada m: n. Por lo tanto, las coordenadas del punto R que divide el segmento de línea que une dos puntos P (x1, y1, z1) y Q (x2, y2, z2) internamente en la relación m: n se pueden calcular mediante la fórmula,

\left( \frac{mx_2 + nx_1}{m+n},\frac{my_2 + ny_1}{m+n},\frac{mz_2 + nz_1}{m+n} \right)

Si el punto R divide a PQ externamente en la razón m: n, entonces sus coordenadas se obtienen reemplazando n por – n, y la fórmula del mismo es,

\left( \frac{mx_2 - nx_1}{m-n},\frac{my_2 - ny_1}{m-n},\frac{mz_2 - nz_1}{m-n} \right)

Caso 1: Coordenadas del punto medio: En caso de que R sea el punto medio de PQ, entonces m : n = 1 : 1 tal que

x =  \frac{x_1 + x_2}{2} , y =  \frac{y_1 + y_2}{2}  y z = \frac{z_1 + z_2}{2}

Estas son las coordenadas del punto medio del segmento que une P (x1, y1, z1) y Q (x2, y2, z2). 

Caso 2: Las coordenadas del punto R que divide a PQ en la razón k: 1 se obtienen tomando k= \frac{m}{n}  que son las siguientes,

\left( \frac{kx_2 + x_1}{k+1},\frac{ky_2 + y_1}{k+1},\frac{kz_2 + z_1}{k+1} \right)

Ejemplo 1: Encuentra las coordenadas del punto que divide el segmento de recta que une los puntos (1, –2, 3) y (3, 4, –5) en la razón 2 : 3 (i) internamente, y (ii) externamente ?

Solución: 

(i) Sea P (x, y, z) el punto que divide el segmento de recta que une A(1, – 2, 3)

y B (3, 4, –5) internamente en la razón 2 : 3. Por lo tanto

\frac{2(3)+3(1)}{2+3} = \frac{9}{5} \\ \frac{2(4)+3(-2)}{2+3} = \frac{2}{5} \\ \frac{2(-5)+3(3)}{2+3} = \frac{-1}{5}

Por lo tanto, el punto requerido es (\frac{9}{5},\frac{2}{5},\frac{-1}{5})

(ii) Sea P (x, y, z) el punto que divide al segmento que une A (1, –2, 3) y

B (3, 4, –5) externamente en la razón 2 : 3. Entonces,

\frac{2(3)+(-3)(1)}{2+(-3)} = -3 \\ \frac{2(4)+(-3)(-2)}{2+(-3)} = -14 \\ \frac{2(-5)+(-3)(3)}{2+(-3)} = 19

Por lo tanto, el punto requerido es (–3, –14, 19). 

Ejemplo 2: usando la fórmula de la sección, demuestre que los tres puntos (– 4, 6, 10), (2, 4, 6) y (14, 0, –2) son colineales.

Solución:

Sean A (– 4, 6, 10), B (2, 4, 6) y C(14, 0, – 2) los puntos dados. Deja el

el punto P divide a AB en la razón k: 1. Entonces las coordenadas del punto P son

(\frac{2k-4}{k+1},\frac{4k+6}{k+1},\frac{6k+10}{k+1})

Examinemos si, para algún valor de k, el punto P coincide con el punto C.

Al poner  \frac{2k-4}{k+1}=14\\ k=\frac{-3}{2} , Cuando k= \frac{-3}{2} entonces,

\frac{4k+6}{k+1} =\frac{4 (-\frac{3}{2})+6}{(-\frac{3}{2})+1}=0 \\ and\\ \frac{6k+10}{k+1} =\frac{6 (-\frac{3}{2})+10}{(-\frac{3}{2})+1}=-2 \\

Por tanto, C (14, 0, –2) es un punto que divide exteriormente a AB en la razón 3:2 y es

igual que P. Por lo tanto, A, B, C son colineales. 

Publicación traducida automáticamente

Artículo escrito por nikitadabral30 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *