Una elipse es el lugar geométrico de todos los puntos en un plano con distancias constantes de dos puntos fijos en el plano. Las ubicaciones fijas rodeadas por la curva se conocen como focos (foco singular). La razón constante es la excentricidad de la elipse y la recta es la directriz. La excentricidad es un factor de elipse que muestra elongación y se simboliza con la letra ‘e’.
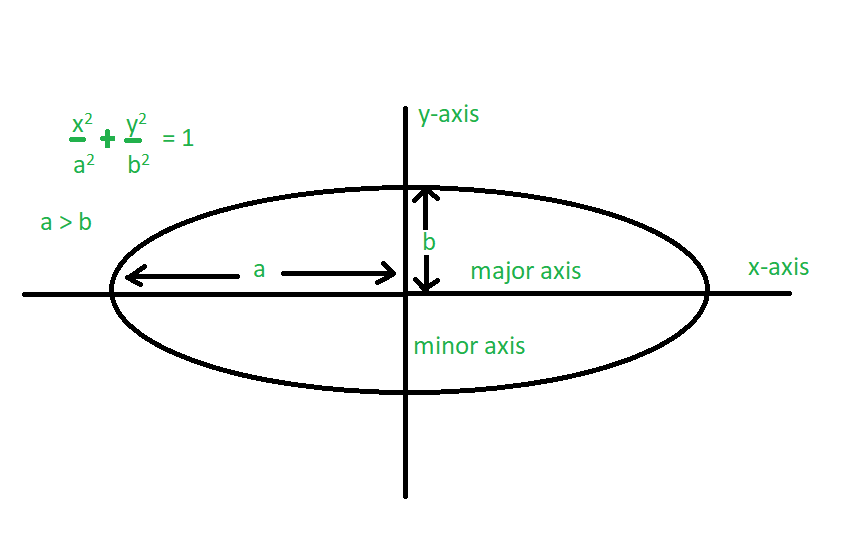
La elipse tiene una forma ovalada y el área de una elipse se especifica por sus ejes mayor y menor. Área de elipse = πab, donde a y b son las longitudes de los ejes semi-mayor y semi-menor de una elipse. La elipse es análoga a otras partes de la sección cónica que tienen formas abiertas y sin límites, como la parábola y la hipérbola. En términos de lugar geométrico, una elipse es el conjunto de todos los puntos en un plano XY cuya distancia desde dos puntos fijos (llamados focos) suma un valor constante. La elipse es un tipo de sección cónica que se forma cuando un plano corta un cono en ángulo con su base. Se forma un círculo cuando el plano corta al cono paralelo a su base.
¿Qué es Elipse?
En geometría, una elipse es una forma bidimensional descrita a lo largo de sus ejes. Cuando un cono es intersecado por un plano en un ángulo con respecto a su base, se crea una elipse. Hay dos puntos focales. El total de las dos distancias al punto focal siempre es constante para todos los lugares a lo largo de la curva. Un círculo es también una elipse en la que los focos están todos en el mismo lugar, que es el centro del círculo.
Propiedades de la elipse:
- Ellipse incluye dos puntos focales, también conocidos como focos.
- Una distancia fija se denomina directriz.
- La excentricidad de una elipse varía de 0 a 1. 0≤e<1
- La suma total de cada distancia desde el lugar geométrico de una elipse a sus dos puntos focales es constante.
- La elipse tiene un eje mayor y uno menor, así como un centro.
Componentes de una elipse:
- Eje (mayor y menor): las elipses se distinguen por dos ejes que se ejecutan a lo largo de los ejes x e y:
- Eje Mayor: El eje mayor es el diámetro más largo de la elipse, pasando por el centro de un extremo al otro en la parte más ancha de la elipse.
- Eje menor: El eje menor es el diámetro más corto de una elipse que atraviesa el centro en su punto más estrecho. La mitad del eje mayor es el semieje mayor, y la mitad del eje menor es el semieje menor.
- Excentricidad de la elipse: la excentricidad de una elipse se define como la relación de distancias desde el centro de la elipse hasta el semieje mayor de la elipse.
e = c/a
dónde
- c es la distancia focal y
- a es la longitud del semieje mayor.
Como ca, la excentricidad de una elipse siempre es mayor que 1.
Además, c 2 = a 2 – b 2.
Como resultado, la excentricidad se convierte en:
mi = √[(a 2 – b 2 )/a 2 ]
e = √[1-(b 2 /a 2 )]
Fórmula de elipse
Tome un punto P en un extremo del eje mayor, como se indica. Como resultado, el total de las distancias entre el punto P y los focos es,
F 1 PAG + F 2 PAG = F 1 O + OP + F 2 PAG = c + a + (a–c) = 2a
Luego, seleccione un punto Q en un extremo del eje menor. La suma de las distancias entre Q y los focos es ahora,
F 1 Q + F 2 Q = √ (segundo 2 + c 2 ) + √ (segundo 2 + c 2 ) = 2√ (segundo 2 + c 2 )
Ya sabemos que los puntos P y Q están en la elipse. En consecuencia, por definición, tenemos
2√ (b 2 + c 2 ) = 2a
entonces √ (b 2 + c 2 ) = un
es decir, a 2 = b 2 + c 2 o c 2 = a 2 – b 2
La siguiente es la ecuación para la elipse.
do 2 = un 2 – segundo 2
Ecuaciones estándar para elipse
La ecuación de la elipse con su centro en el origen y su eje mayor a lo largo del eje x es:
x 2 /a 2 + y 2 /b 2 = 1
donde –a ≤ x ≤ a.
La ecuación de la elipse con el centro en el origen y el eje mayor a lo largo del eje y es:
x 2 /b 2 +y 2 /a 2 = 1
donde –b ≤ y ≤ b.
Ejemplos de preguntas
Pregunta 1: Si la longitud del semieje mayor es de 10 cm y la del semieje menor es de 7 cm de una elipse. Encuentra su área.
Responder:
Dada la longitud del semieje mayor de una elipse, a = 10 cm
Longitud del semieje menor de una elipse, b = 7 cm
Conocemos el área de una elipse usando la fórmula;
Área = π xaxb
= π x 10 x 7
= 70 x pi
Por lo tanto Área = 219.91 cm 2
Pregunta 2: ¿Define el eje mayor y menor de una elipse?
Responder:
Las elipses se distinguen por dos ejes que corren a lo largo de los ejes x e y:
- Eje Mayor: El eje mayor es el diámetro más largo de la elipse, pasando por el centro de un extremo al otro en la parte más ancha de la elipse.
- Eje menor: El eje menor es el diámetro más corto de una elipse que atraviesa el centro en su punto más estrecho. La mitad del eje mayor es el semieje mayor, y la mitad del eje menor es el semieje menor.
Pregunta 3: ¿Cuáles son las ecuaciones de Ellipse?
Responder:
La ecuación de la elipse con su centro en el origen y su eje mayor a lo largo del eje x es:
x 2 /a 2 + y 2 /b 2 = 1
donde –a ≤ x ≤ a.
La ecuación de la elipse con el centro en el origen y el eje mayor a lo largo del eje y es:
x 2 /b 2 +y 2 /a 2 = 1
Pregunta 4: Encuentra las longitudes para el eje mayor y el eje menor de la ecuación 7x 2 +3y 2 = 21
Responder:
La ecuación dada es 7x 2 +3y 2 = 21
dividiendo ambos lados por 21, obtenemos
x2 /3 + y2 / 7 = 1
conocemos la ecuación estándar de la elipse
x 2 /b 2 +y 2 /a 2 = 1
como los focos se encuentran en el eje y, para la ecuación anterior, la elipse centrada en el origen y el eje mayor en el eje y.
después ;
b 2 = 3, lo que significa b = 1.73
a 2 = 7, lo que significa a = 2,64
por lo tanto
sea la longitud del eje mayor = 2a = 5.28
longitud del eje menor = 2b = 3,46
Pregunta 5: ¿Cuál será el área de una elipse?
Responder:
El área de una elipse está determinada por las longitudes de sus ejes mayor y menor.
Área de la elipse = π.ab