Fórmula de la media armónica

Las estadísticas se ocupan del análisis de datos y presentan los datos/valores de manera organizada. Para representar datos en una serie estadística usamos el concepto de tendencia central. La medida de tendencia central es un valor que describe el grupo de grupos de datos en torno a un valor central. Es el centro de un conjunto de datos.

Hay tres medidas de tendencia central,

Significar
Mediana
Modo

Ahora conozcamos un tipo importante de media llamada Media Armónica.

Significado armonico

La media armónica se define como el recíproco del promedio del recíproco de todos los valores de datos. Da menos ponderación a los valores más grandes y mayor ponderación a los valores más pequeños. Esta media armónica se utiliza principalmente en el sector financiero.

Sea x ₁ , x ₂ , x ₃ , x ₄ , … x _n los datos dados, entonces la media armónica de los datos dados se puede calcular mediante la fórmula:

Media armónica (HM) = $\frac{n}{(1/x_1)+(1/x_2)+(1/x_3)+(1/x_4)+...+(1/x_n)}$

Prueba

La media armónica es la inversa de la media aritmética de los términos de datos recíprocos.

Entonces, la media aritmética de los datos x ₁ , x ₂ , x ₃ , …, x _n es,

Media aritmética = $\frac{x_1+x_2+x_3+...+x_n}{n}$

En la media armónica consideramos el recíproco de los valores de los datos.

Entonces, la media aritmética de los datos recíprocos 1/x ₁ , 1/x ₂ , 1/x ₃ , …, 1/x _n es,

Media aritmética para datos recíprocos = $\frac{(1/x_1)+(1/x_2)+(1/x_3)+...+(1/x_n)}{n}$ ->(1)

Se sabe que la media armónica es inversa a la media aritmética de valores de datos recíprocos de-(1)

Media armónica = Media aritmética de datos recíprocos ^-1

= $(\frac{(1/x_1)+(1/x_2)+(1/x_3)+...+(1/x_n)}{n})^{-1}$

= $\frac{n}{(1/x_1)+(1/x_2)+(1/x_3)+...+(1/x_n)}$

Media armónica ponderada

Es similar a la media armónica pero, además, tiene pesos. Si los pesos son iguales a 1, entonces es lo mismo que la media armónica. La media armónica ponderada se calcula para el conjunto dado de pesos w ₁ ,w ₂ ,w ₃ ,w ₄ ,…,w _n y los datos x ₁ , x ₂ , x ₃ , x ₄ , …, x _n es,

Media armónica ponderada = 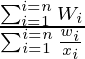$\frac{\sum_{i=1}^{i=n}W_i}{\sum_{i=1}^{i=n}\frac{w_i}{x_i}}$

Veamos la relación entre los tipos de medios,

Relación entre la media aritmética , la media armónica y la media geométrica

Para los datos x ₁ , x ₂ , x ₃ , x ₄ , …, x _n ,

Media aritmética = (x ₁ + x ₂ + x ₃ + x ₄ +….+ x _n )/n

Media Armónica = n/((1/x ₁ ) + (1/x ₂ ) + (1/x ₃ ) + (1/x ₄ ) + … + (1/x _n ))

Media geométrica = n√(x ₁ + x ₂ + x ₃ + x ₄ + … + x _n )

A partir de estas fórmulas podemos escribirlo como,

Media geométrica = √(Media aritmética × Media armónica)

Media geométrica ² = Media aritmética × Media armónica

De la fórmula anterior,

Media Armónica = Media Geométrica ² / Media Aritmética

Veamos algunos ejemplos de cómo encontrar la media armónica,

Problemas de muestra

Pregunta 1: ¿Cuál es la media armónica de los datos 10, 20, 5, 15, 10?

Solución:

datos dados

10, 20, 5, 15, 10

n = 5 (ya que el tamaño total es 5)

Media armónica= $\frac{n}{(1/x_1)+(1/x_2)+(1/x_3)+(1/x_4)+...+(1/x_n)}$

= $\frac{5}{(1/10)+(1/20)+(1/5)+(1/15)+(1/10)}$

= 5/(0,1 + 0,05 + 0,2 + 0,06 + 0,1)

= 5/0,51

= 9,8

Por lo tanto, la media armónica para los datos dados es 9.8

Pregunta 2: ¿Cuál es la media armónica de los datos 100, 50, 75, 25?

Solución:

datos dados

100, 50, 75, 25

n = 4 (ya que el tamaño total es 4)

Media armónica= $/frac{n}/{(1/x_1)+(1/x_2)+(1/x_3)+(1/x_4)+...+(1/x_n)}$

= $\frac{4}{(1/100)+(1/50)+(1/75)+(1/25)}$

= 4/(0,01+0,02+0,013+0,04)

= 4/0.083

= 48,2

Por lo tanto, la media armónica para los datos dados es 48.2

Pregunta 3: ¿Cuál es la media armónica de los datos 1, 5, 3?

Solución:

datos dados

1, 5, 3

n = 3 (ya que el tamaño total es 3)

Media armónica= $\frac{n}{(1/x_1)+(1/x_2)+(1/x_3)+(1/x_4)+...+(1/x_n)}$

= $\frac{3}{(1/1)+(1/5)+(1/3)}$

= 3/(1 + 0,2 + 0,33)

= 3/1,53

= 1,96

Por lo tanto, la media armónica para los datos dados es 1.96

Pregunta 4: ¿Cuál es la media armónica si la media aritmética es 10 y la media geométrica es 7?

Solución:

Dado,

Media aritmética (AM) = 10

Media Geométrica (GM) = 7

Media Armónica = GM ² /AM

= 7 ² /10

= 49/10

= 4,9

Por lo tanto, la media armónica de la media aritmética y geométrica dada es 4.9

Pregunta 5: ¿Cuál es la media geométrica si la media aritmética es 20 y la media armónica es 15?

Solución:

Dado

Media aritmética (AM) = 20

Media armónica (HM) = 15

Media Geométrica = √(Media Aritmética × Media Armónica)

= √(20 × 15)

= √300

= 17,32

Por lo tanto, la media geométrica de la media aritmética y armónica dada es 17.32

Pregunta 6: ¿Cuál es la media armónica ponderada de los datos dados?

Peso (ancho)	Datos(x)
1	20
2	30
3	10
2	15

Solución:

Encuentre la suma de pesos, es decir, ∑w _i , 1/x y w/x y ∑w/x

Pesos (ancho)

X

1/x

w/x

1

20

0.05

0.05

2

30

0.03

0.06

3

10

0.1

0.3

2

15

0.06

0.12

∑w=8

∑w/x=0.53

Media armónica _w = ∑w/∑w/x

= 8/0,53

= 15,09

La media armónica ponderada para los datos dados es 15.09

Pregunta 7: ¿Cuál es la media armónica ponderada para los datos dados?

X	10	15	20	25	30
w	2	3	4	5	1

Solución:

Encuentre la suma de pesos, es decir, ∑w _i , 1/x y w/x y ∑w/x

X

w

1/x

w/x

10

2

0.1

0.2

15

3

0.066

0.198

20

4

0.05

0.2

25

5

0.04

0.2

30

1

0.033

0.033

∑w = 15

∑w/x = 0,831

Media armónica _w = ∑w/∑w/x

= 15/0,831

= 18,05

La media armónica ponderada para los datos dados es 18.05

Publicación traducida automáticamente

Artículo escrito por akhilvasabhaktula03 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Significado armonico

Media armónica ponderada

Problemas de muestra

Deja una respuesta Cancelar la respuesta