La raíz cuadrada media se define como la media cuadrática o un subconjunto de la media generalizada con un exponente de 2. En otras palabras, la raíz cuadrada de la suma total de los cuadrados de cada valor de datos en una observación se calcula usando la raíz media fórmula cuadrada. Puede interpretarse como una función cambiante basada en una integral de los cuadrados de los valores que son instantáneos en un ciclo. Se utiliza aquí para calcular la raíz cuadrada de la media aritmética del cuadrado de la función que describe la forma de onda continua. Se abrevia como RMS.
Fórmula
Para un conjunto de datos de n valores, es decir, {x 1 , x 2 , x 3 ,…. x n }, el valor de la raíz cuadrada media se da como,
Aquí, X RMS es el valor cuadrático medio de las n observaciones dadas del conjunto de datos.
Para una función continua f(t), definida en el intervalo [T 1 , T 2 ], el valor de la raíz cuadrática media se da como,
Aquí, X RMS es el valor cuadrático medio de la función f(t) tal que T 1 ≤ t ≤ T 2 .
Problemas de muestra
Problema 1. Calcular la raíz cuadrada media del conjunto de datos: 2, 7, 3, 5, 1.
Solución:
Usando la fórmula que obtenemos,
= √(88/5)
= √(17.6)
= 4,2
Problema 2. Calcular la raíz cuadrada media del conjunto de datos: 10, 12, 9, 3, 6.
Solución:
Usando la fórmula que obtenemos,
= √(370/5)
= √(74)
= 8,6
Problema 3. Calcular la raíz cuadrada media del conjunto de datos: 5, 7, 2, 4, 3, 9.
Solución:
Usando la fórmula que obtenemos,
= √(184/6)
= √(30.66)
= 5,53
Problema 4. Calcular la raíz cuadrada media del conjunto de datos: 3, 6, 9, 12, 15, 18, 20.
Solución:
Usando la fórmula que obtenemos,
= √(1219/7)
= √(174,14)
= 13.196
Problema 5. Calcule la raíz cuadrada media del conjunto de datos si la suma de los cuadrados de las observaciones del conjunto de datos es 216 y el número de observaciones es 6.
Solución:
Tenemos,
S = 216
norte = 6
Usando la fórmula que obtenemos,
R = √(S/n)
= √(216/6)
= √(36)
= 6
Problema 6. Calcule la raíz cuadrática media del conjunto de datos si la suma de los cuadrados de las observaciones del conjunto de datos es 5832 y el número de observaciones es 18.
Solución:
Tenemos,
S = 5832
n = 18
Usando la fórmula que obtenemos,
R = √(S/n)
= √(5832/18)
= √(324)
= 18
Problema 7. Calcular el valor cuadrático medio de la función continua f(t) = t en el intervalo [4, 7].
Solución:
Tenemos,
f(t) = t y 4 ≤ t ≤ 7.
Usando la fórmula que obtenemos,
= √(343/9 – 64/9)
= √(279/9)
= √(31)
= 5,56
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
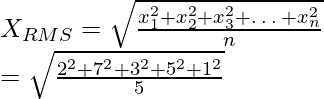

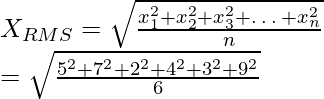

![Rendered by QuickLaTeX.com X_{RMS}=\sqrt{\frac{1}{T_{2}-T_{1}}\int_{T_{1}}^{T_{2}}[f\left ( t \right )^{2}dt}]\\ =\sqrt{\frac{1}{7-4}\int_{4}^{7}[t^{2}dt}]\\ =\sqrt{\frac{1}{3}[\frac{t^3}{3}]^{7}_4}\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e3c4c2ed0c780b9f08334edf7e94f194_l3.png)