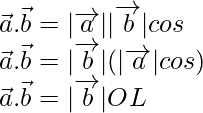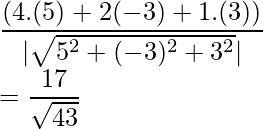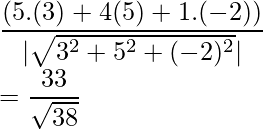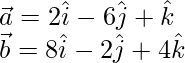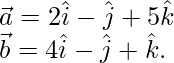Fórmula de proyección vectorial

Un vector es un objeto bidimensional que tiene tanto magnitud como dirección. Un vector se puede ver geométricamente como un segmento de línea dirigido con una flecha que indica la dirección del vector y una longitud igual a la magnitud del vector. De la cola a la cabeza es la dirección del vector. Dos vectores son iguales si tienen la misma magnitud y dirección. Esto significa que si trasladamos un vector a un nuevo punto (sin girarlo), el vector que derivamos es el mismo con el que comenzamos.

Vector de proyección

La longitud de la sombra de un vector dado proyectada sobre otro vector es la proyección vectorial de un vector sobre otro vector. Se calcula multiplicando la magnitud de los dos vectores por la cosecante del ángulo entre ellos. Un valor escalar es el resultado de una fórmula de proyección vectorial.

Fórmula

El producto escalar del vector a y el vector b, dividido por la magnitud del vector b, es la fórmula del vector de proyección en álgebra vectorial para la proyección de un vector a sobre el vector b. El resultado del producto escalar es un valor escalar y la magnitud del vector b también es un valor escalar. Como resultado, la magnitud y el argumento de la respuesta del vector de proyección son valores escalares en la dirección del vector b.

Proyección del Vector a sobre el Vector b = $\frac{\vec{a}.\vec{b}}{|b|}$

Derivación

Del triángulo rectángulo OAL, cos θ = OL/OA

OL = OA cos θ

⇒ OL = $\vec{a}$ cos θ

OL es el vector de proyección del vector a sobre el vector b.

Sabemos, $\vec{a}.\vec{b}=|\overrightarrow a||\overrightarrow b|cos θ$

$\vec{a}.\vec{b}=|\overrightarrow a||\overrightarrow b|cos θ\\ \vec{a}.\vec{b}=|\overrightarrow b|(|\overrightarrow a|cos θ)\\\vec{a}.\vec{b}=|\overrightarrow b|OL$

OL = $\frac{\vec{a}.\vec{b}}{|b|}$

Por lo tanto probado.

Problemas de muestra

Pregunta 1. Encuentra la proyección del vector $4\hat i + 2\hat j + \hat k$ y $5\hat i -3\hat j + 3\hat k$ .

Solución:

Aquí, $\vec{a}=4\hat i + 2\hat j + \hat k \\\vec{b}=5\hat i -3\hat j + 3\hat k$ .

Sabemos, proyección del Vector a sobre el Vector b = $\frac{\vec{a}.\vec{b}}{|b|}$

$\dfrac{(4.(5) + 2(-3) + 1.(3))}{|\sqrt{5^2 + (-3)^2 + 3^2}|}\\=\dfrac{17}{\sqrt{43}}$

Pregunta 2. Encuentra la proyección del vector $5\hat i + 4\hat j + \hat k$ y $3\hat i + 5\hat j - 2\hat k$ .

Solución:

Aquí, $\vec{a}=5\hat i + 4\hat j + \hat k \\\vec{b}=3\hat i + 5\hat j - 2\hat k.$

Sabemos, proyección del Vector a sobre el Vector b = $\frac{\vec{a}.\vec{b}}{|b|}$

$\dfrac{(5.(3) + 4(5) + 1.(-2))}{|\sqrt{3^2 + 5^2 + (-2)^2}|}\\=\dfrac{33}{\sqrt{38}}$

Pregunta 3. Encuentra la proyección del vector $5\hat i - 4\hat j + \hat k$ y $3\hat i - 2\hat j + 4\hat k$ .

Solución:

Aquí, $\vec{a}=5\hat i - 4\hat j + \hat k \\\vec{b}=3\hat i - 2\hat j + 4\hat k.$

Sabemos, proyección del Vector a sobre el Vector b = $\frac{\vec{a}.\vec{b}}{|b|}$

$\dfrac{(5.(3) + 4(5) + 1.(-2))}{|\sqrt{3^2 + 5^2 + (-2)^2}|}\\=\dfrac{27}{\sqrt{29}}$

Pregunta 4. Encuentra la proyección del vector 2\hat i – 6\hat j + \hat k y 8\hat i – 2\hat j + 4\hat k.

Solución:

Aquí, $\vec{a}=2\hat i - 6\hat j + \hat k \\\vec{b}=8\hat i - 2\hat j + 4\hat k$

Sabemos, proyección del Vector a sobre el Vector b = $\frac{\vec{a}.\vec{b}}{|b|}$

$\dfrac{(5.(3) + 4(5) + 1.(-2))}{|\sqrt{3^2 + 5^2 + (-2)^2}|}\\=\dfrac{57}{\sqrt{69}}$

Pregunta 5. Encuentra la proyección del vector 2\hat i – \hat j + 5\hat k y 4\hat i – \hat j + \hat k.

Solución:

Aquí, $\vec{a}=2\hat i - \hat j + 5\hat k \\\vec{b}=4\hat i - \hat j + \hat k.$

Sabemos, proyección del Vector a sobre el Vector b = $\frac{\vec{a}.\vec{b}}{|b|}$

$\dfrac{(5.(3) + 4(5) + 1.(-2))}{|\sqrt{3^2 + 5^2 + (-2)^2}|}\\=\dfrac{27}{\sqrt{29}}$

Publicación traducida automáticamente

Artículo escrito por parmaramolaksingh1955 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Vector de proyección

Problemas de muestra

Deja una respuesta Cancelar la respuesta