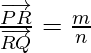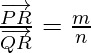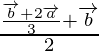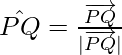Las cantidades físicas se dividen en dos categorías: cantidades escalares y vectoriales. Las cantidades que solo tienen magnitud y no una dirección fija se llaman cantidades escalares . P.ej. Masa, volumen, densidad, etc. Cantidades que tienen tanto magnitud como dirección. Tales cantidades se denominan cantidades vectoriales o vectores. P.ej. Desplazamiento, velocidad, aceleración, cantidad de movimiento, etc.
Los vectores están representados por segmentos de línea que están dirigidos, como la dirección de una flecha marcada en un extremo, que denota dirección y la longitud del segmento de línea es la magnitud del vector. P.ej. ![]()
Denota dos puntos A y B, tales que la magnitud del vector es la longitud de la línea recta AB y su dirección es de A a B. Aquí, el punto A se llama el punto inicial del vector ![]() y el punto B se llama el terminal punto (o punto final).
y el punto B se llama el terminal punto (o punto final).
La magnitud o módulo de un vector \overrightarrow{AB} es un número positivo (>0) que es la medida de su longitud y se denota por |\overrightarrow{AB}|.

Tipos de vectores
vector cero
Un vector cuyos puntos inicial y terminal (extremo) coinciden entre sí se denomina vector cero (o vector nulo) y se denota como ![]() . Al vector cero no se le puede asignar una dirección definida ya que tiene magnitud cero. O, en otras palabras, puede definirse como si tuviera cualquier dirección.
. Al vector cero no se le puede asignar una dirección definida ya que tiene magnitud cero. O, en otras palabras, puede definirse como si tuviera cualquier dirección.
Los vectores ![]() ,
, ![]() representan el vector cero.
representan el vector cero.
Vector unitario
Un vector cuya magnitud es la unidad (=1) se llama vector unitario . El vector unitario ![]() se denota por
se denota por ![]()
y ![]() = 1
= 1

Vectores Coiniciales
Dos o más vectores que tienen el mismo punto inicial o punto de partida se denominan vectores coiniciales.
Vectores colineales
Si dos o más vectores son paralelos entre sí, independientemente de sus magnitudes y direcciones. Entonces se llamarán vectores colineales.
Vectores iguales
Si dos vectores ![]() y
y ![]() tienen la misma magnitud y dirección independientemente de las posiciones de sus puntos iniciales se llamarán vectores iguales, y se puede representar como
tienen la misma magnitud y dirección independientemente de las posiciones de sus puntos iniciales se llamarán vectores iguales, y se puede representar como ![]()
Negativo de un vector
Un vector cuya magnitud (longitud) es igual a la del vector dado (digamos ![]() ) pero la dirección es opuesta a la de él (los puntos inicial y terminal están invertidos), se llama negativo del vector dado.
) pero la dirección es opuesta a la de él (los puntos inicial y terminal están invertidos), se llama negativo del vector dado.
Por ejemplo, vector ![]() es negativo del vector
es negativo del vector ![]() y se escribe como,
y se escribe como, ![]()
Vector de posición
Considere un punto P en el espacio 3D, con coordenadas como (x, y, z) con respecto al origen O (0, 0, 0). Y, el vector ![]() que tiene O como punto inicial y P como punto terminal se llama vector de posición del punto P con respecto a O.
que tiene O como punto inicial y P como punto terminal se llama vector de posición del punto P con respecto a O.

Usando la fórmula de la distancia, la magnitud (o longitud) de ![]() es
es
![]() =
= ![]()
![]()
Nota: La definición de vector definida anteriormente es un tipo de vector que puede estar sujeto a su desplazamiento paralelo sin cambiar su magnitud y dirección. Dichos vectores se denominan vectores libres.
Suma de vectores
Un vector ![]() simplemente denota el desplazamiento de cualquier cosa desde el punto A al punto B.
simplemente denota el desplazamiento de cualquier cosa desde el punto A al punto B.
Ley del triángulo de la suma de vectores
Considere una situación en la que una persona se mueve de A a B y luego de B a C. El desplazamiento neto realizado por la persona del punto A al punto C está dado por el vector y expresado como

Esto se conoce como la ley del triángulo de la suma de vectores .
Como,
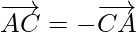
Cuando los lados de un triángulo se toman en orden, conduce a cero resultante (sin resultado de desplazamiento) ya que los puntos inicial y terminal coinciden entre sí.
Ley del paralelogramo de la suma de vectores
Si dos vectores ![]() y
y ![]() están representados en magnitud y dirección por los dos lados adyacentes del paralelogramo, entonces su suma (
están representados en magnitud y dirección por los dos lados adyacentes del paralelogramo, entonces su suma ( ![]() )
) ![]() está representada por las diagonales del paralelogramo dado que es coinicial con los vectores dados
está representada por las diagonales del paralelogramo dado que es coinicial con los vectores dados ![]() y
y ![]() .
.
Ahora, consideremos el paralelogramo ABCD
donde,
y
entonces usando la ley del triángulo de la suma de vectores, del triángulo ABC, tenemos
………………….(1)
Ahora bien, como los lados opuestos de un paralelogramo son iguales y paralelos
y
Nuevamente usando la ley del triángulo de la suma de vectores, del triángulo ADC, tenemos
………………………….(2)
De (1) y (2), obtenemos la propiedad conmutativa
Nota: La magnitud
no es igual a la suma de la magnitud (longitud) de
y
.
(ii) Propiedad asociativa

Usando la ley del triángulo, del triángulo PQR, tenemos
Usando la ley del triángulo, del triángulo QRS, tenemos
Usando la ley del triángulo, del triángulo PRS, tenemos
Usando la ley del triángulo, del triángulo PQS, tenemos
Por eso,
(iii) Identidad aditiva
Para cualquier vector
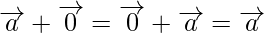
(iv) Inverso aditivo
Para cualquier vector
Problema 1: Si ![]() , demuestre que los puntos P, Q y R son colineales.
, demuestre que los puntos P, Q y R son colineales.
Solución:
Tenemos,
Usando, a la inversa de la ley del triángulo de la suma de vectores, obtenemos
y
ae paralelo o colineal. Pero, Q es un punto común a ellos.
Entonces,
y
son colineales. Por tanto, los puntos P, Q, R son colineales.
Problema 2: B, P, Q, R y A son cinco puntos en un plano. Demuestre que la suma de los vectores ![]() y
y ![]() en 3
en 3 ![]() .
.
Solución:
Usando la suma de vectores de la ley del triángulo en △APB
……………(1)
Usando la suma de vectores de la ley del triángulo en △AQB
…………………..(2)
Usando la suma de vectores de la ley del triángulo en △ARB
…………….(3)
Sumando (1), (2) y (3), obtenemos
Por lo tanto, la suma de los vectores es 3
Problema 3: Sea O el centro de un hexágono regular CDEFAB. Encuentre la suma de los vectores ![]() y
y ![]() .
.
Solución:
Como establece la propiedad del hexágono, el centro de un hexágono regular biseca todas las diagonales que lo atraviesan.
Asi que,
y
………………..(1)
…………………..(2)
…………………..(3)
Sumando (1), (2) y (3), obtenemos
Fórmula de sección
Aquí, los puntos P y Q son los dos puntos representados por los vectores de posición ![]() y
y ![]() , respectivamente, con respecto al origen O. Entonces el segmento de recta que une los puntos P y Q se puede dividir por un tercer punto, aquí decimos R, de dos maneras de la siguiente manera:
, respectivamente, con respecto al origen O. Entonces el segmento de recta que une los puntos P y Q se puede dividir por un tercer punto, aquí decimos R, de dos maneras de la siguiente manera:
Aquí, pretendemos encontrar el vector de posición ![]() para el punto R con respecto al origen O. Tomamos los dos casos uno por uno.
para el punto R con respecto al origen O. Tomamos los dos casos uno por uno.
Internamente

Cuando R divide a PQ internamente. Si R divide
tal que
donde m y n son valores positivos, especificamos que el punto R se divide
internamente en la razón de m : n.
Ahora de los triángulos ORQ y OPR, tenemos
Por lo tanto, podemos concluir que,
metro
= norte
Por simplificación, obtenemos
Cuando R es el punto medio PQ
entonces m = norte
Entonces, obtenemos
Externamente

Cuando R divide a PQ externamente. Si R divide
tal que
donde myn son valores positivos, decimos que el punto R se divide
externamente en la razón de m : n.
Ahora de los triángulos ORQ y OPR, tenemos
Por lo tanto, podemos concluir que,
Por simplificación, obtenemos
Problema 1: Encuentra los vectores de posición de los puntos que dividen la unión de los puntos interna ![]() y
y ![]() externamente en la razón 2 : 3.
externamente en la razón 2 : 3.
Solución:
Sean A y B los puntos dados con los vectores de posición
y
respectivamente.
Sea P dividiendo el
en la razón 2 : 3 internamente
m = 2 y n = 3
Usando fórmula de sección interna,
Vector de posición de P =
Vector de posición de P =
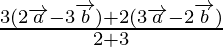
Vector de posición de P =
Vector de posición de P =
Ahora, sea P el que divida
en la razón 2 : 3 externamente
m = 2 y n = 3
Usando fórmula de sección externa,
Vector de posición de P =
Vector de posición de P =
Vector de posición de P =
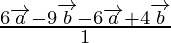
Vector de posición de P =
Problema 2: Si ![]() y
y ![]() son vectores de posición de los puntos A y B respectivamente, entonces encuentre el vector de posición de los puntos de trisección de AB.
son vectores de posición de los puntos A y B respectivamente, entonces encuentre el vector de posición de los puntos de trisección de AB.
Solución:
Sean P y Q puntos de trisección. Entonces, AP = PQ = QB = k (variable constante)
PB = PQ + QB = k + k = 2k
P divide a AB en la razón 1 : 2
Usando fórmula de sección interna, donde m=1 y n=2
Vector de posición de P =
Vector de posición de P =
Vector de posición de P =
Ahora, podemos ver claramente que Q es el punto medio de PB.
Aplique la fórmula de la sección del punto medio que tenemos,
Vector de posición de Q =
Vector de posición de Q =
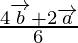
Vector de posición de Q =
Problema 3: Si D es el punto medio del lado BC de un triángulo ABC, demuestre que ![]()
Solución:
Sea A el origen aquí y los vectores de posición de B y C sean
y
respectivamente.
Como D es el punto medio de BC.
Aplicando la fórmula de la sección del punto medio, obtenemos
Vector de posición de D =
Como,
Por lo tanto, Probado!!
Componentes de un vector
Tomemos los puntos A(1, 0, 0), B(0, 1, 0) y C(0, 0, 1) en el eje x, eje y y eje z, respectivamente. Después,

![]() = 1,
= 1, ![]() = 1 and
= 1 and ![]() = 1
= 1
Los vectores, ![]() ,
, ![]() y
y ![]() tienen magnitud la unidad o 1, que se denominan vectores unitarios a lo largo de los ejes OX, OY y OZ, respectivamente, y se denotan por
tienen magnitud la unidad o 1, que se denominan vectores unitarios a lo largo de los ejes OX, OY y OZ, respectivamente, y se denotan por ![]() ,
, ![]() y
y ![]() respectivamente.
respectivamente.
Consideremos el vector de posición ![]() de un punto P(x, y, z). Sea P 1 el pie de la perpendicular desde P en el plano XY.
de un punto P(x, y, z). Sea P 1 el pie de la perpendicular desde P en el plano XY.

Por lo tanto, vemos que P 1 P es paralelo al eje z. Como ![]() ,
, ![]() y
y ![]() son los vectores unitarios a lo largo de los ejes x, y y z, respectivamente, y por la definición de las coordenadas de P, tenemos
son los vectores unitarios a lo largo de los ejes x, y y z, respectivamente, y por la definición de las coordenadas de P, tenemos
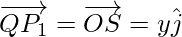
Usando la ley del triángulo, del triángulo OQP 1 , tenemos
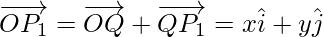
Usando la ley del triángulo, del triángulo OP 1 P, tenemos
Por lo tanto, el vector de posición de P con referencia a O es el siguiente:
Longitud
La longitud del vector
,
OP 1 2 = OQ 2 + QP 1 2 (usando el teorema de Pitágoras)
OP1 2 = x 2 + y 2
y en el triángulo rectángulo OP 1 P, tenemos
OP 2 = OP 1 2 + PP 1 2
OP 2 = x 2 + y 2 + z 2
OP =
Por lo tanto, la longitud del vector
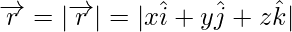
Si ![]() y
y ![]() son dos vectores como
son dos vectores como ![]() y
y ![]() entonces,
entonces,
Suma
Diferencia
Los vectores
, si y si
un 1 = un 2 , segundo 1 = segundo 2 y c 1 = c 2
La multiplicación del vector por cualquier escalar k viene dada por
Vector que une dos puntos
Si P(x 1 , y 1 , z 1 ) y Q(x 2 , y 2 , z 2 ) son dos puntos cualesquiera, entonces el vector que une P y Q es el vector ![]()
Uniendo los puntos P y Q con el origen O, y aplicando la ley del triángulo, del triángulo OPQ, tenemos

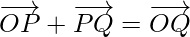
Usando las propiedades de la suma de vectores, la ecuación anterior se convierte en
Por lo tanto, la magnitud de
es la siguiente:
Problema 1: Encuentra el valor de x, y y z para que los vectores ![]() y
y ![]() sean iguales.
sean iguales.
Solución:
Dos vectores
y
son iguales iff
un 1 = un 2 , segundo 1 = segundo 2 y c 1 = c 2
Por lo tanto, los valores de x = 2, y = 2 y z =1.
Problema 2: Encuentra la magnitud del vector ![]()
Solución:
Como, tenemos
= 7
Problema 3: Encuentra el vector unitario del vector dado como ![]()
Solución:
Dejar,
= 7
Entonces, el vector unitario en la dirección de
está dado por,
Problema 4: Encuentra el vector unitario del vector dado como ![]() , donde los puntos P(1,2,3) y Q(4,5,6).
, donde los puntos P(1,2,3) y Q(4,5,6).
Solución:
Vector de posición de P(1,2,3) =
Vector de posición de Q(4,5,6) =
=
–
Ahora, la magnitud de
= 3√3
Entonces, el vector unitario en la dirección de
está dado por,
Problema 5: Demostrar que el vector ![]() y
y ![]() son colineales.
son colineales.
Solución:
Deja,
y
Como podemos ver
Esto implica,
Por lo tanto,
y
son colineales.
Problema 6: si A(2,0,0), B(0,1,0), C (0,0,2) tienen vectores de posición, demuestre que △ABC es un triángulo isósceles.
Solución:
Vector de posición de A(2,0,0) =
Vector de posición de B(0,1,0) =
Vector de posición de C(0,0,2) =
=
Ahora, la magnitud de
=
Ahora, la magnitud de
Claramente, AB = BC.
Por lo tanto, △ABC es un triángulo isósceles.