Fórmula del coeficiente de correlación – Part 1

Los coeficientes de correlación se utilizan para calcular qué tan vital es una conexión entre dos variables. Hay diferentes tipos de coeficientes de correlación, uno de los más populares es la correlación de Pearson (también conocida como R de Pearson) que se usa comúnmente en la regresión lineal.

Coeficiente de correlación Fórmula

El procedimiento del coeficiente de correlación se utiliza para determinar qué tan fuerte es una relación entre los datos. El procedimiento del coeficiente de correlación arroja un valor entre 1 y -1. En el cual,

-1 indica una fuerte relación negativa
1 indica fuertes relaciones positivas
Y un resultado de cero implica ninguna conexión en absoluto

Correlacion positiva

Correlación negativa

Correlación cero

Sentido

Un coeficiente de correlación de -1 significa que hay una disminución negativa de una proporción fija, por cada aumento positivo en una variable. Así, la cantidad de gasolina en un tanque disminuye en perfecta correlación con la velocidad.
Un coeficiente de correlación de 1 significa que hay un aumento positivo de una proporción fija de otros, por cada aumento positivo en una variable. Por ejemplo, el tamaño del zapato aumenta en perfecta correlación con la longitud del pie.
Cero significa que por cada aumento, no hay un aumento positivo ni negativo. Los dos simplemente no están relacionados.

Tipos de fórmulas

Fórmula del coeficiente de correlación de Pearson

$R= \frac{n(∑xy) - (∑x)(∑y)}{\sqrt{[n∑x²-(∑x)²][n∑y²-(∑y)²}}$ $\text{[math]}$

Ejemplo de fórmula de coeficiente de correlación

$r_{xy}= cov(x,y) / s_xs_y$ $\text{[math]}$

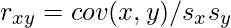
S _xy es la covarianza de la muestra, y S _x y S _y son las desviaciones estándar de la muestra

Fórmula del coeficiente de correlación de la población

$pxy= cov(X,Y) / σxσy$ $\text{[math]}$

Utiliza σ _x y σ _y como la desviación estándar de la población y σ _xy como la covarianza de la población.

correlación de Pearson

Es la correlación más común en estadística. El nombre completo es correlación Producto Momento de Pearson, abreviado PPMC. Muestra la relación lineal entre los dos conjuntos de datos. Se utilizan dos letras para representar la correlación de Pearson: la letra griega rho (ρ) para una población y la letra “r” para un coeficiente de correlación de muestra.

Pasos para encontrar el coeficiente de correlación de Pearson

Paso 1: en primer lugar, haga un gráfico con los datos dados, como el tema, x e y, y agregue tres columnas más en él, xy, x² e y².

Paso 2: ahora multiplica las columnas x e y para llenar la columna xy. Por ejemplo:- en x tenemos 24 y en y tenemos 65 entonces xy será 24×65=1560.

Paso 3: Ahora, toma el cuadrado de los números en la columna x y completa la columna x².

Paso 4: Ahora, tome el cuadrado de los números en la columna y y llene la columna y².

Paso 5: Ahora, sume todos los valores en las columnas y coloque el resultado en la parte inferior. La letra griega sigma (Σ) es la forma abreviada de decir sumatoria.

Paso 6: Ahora, usa la fórmula para el coeficiente de correlación de Pearson:

$R= \frac{n(∑xy) - (∑x)(∑y)}{\sqrt{[n∑x²-(∑x)²][n∑y²-(∑y)²}}$

Para saber que tipo de variable tenemos si es positiva o negativa.

Coeficiente de correlación lineal

El coeficiente de correlación de Pearson es el coeficiente de correlación lineal que devuelve el valor entre -1 y +1. En este -1 indica una fuerte correlación negativa y +1 indica una fuerte correlación positiva. Si es 0 entonces no hay correlación. Esto también se conoce como correlación cero.

Las “estimaciones crudas” para analizar la estabilidad de las correlaciones usando la Correlación de Pearson:

valor r	estimaciones crudas
+.70 o superior	Una relación positiva muy fuerte.
+.40 a +.69	Fuerte relación positiva
+.30 a +.39.	Relación positiva moderada
+.20 a +.29	relación positiva débil
+.01 a +.19	Relación nula o insignificante
0	Sin relación [correlación cero]
-.01 a -.19	Relación nula o insignificante
-.20 a -.29	relación negativa débil
-.30 a -.39	Relación negativa moderada
-.40 a -.69	Fuerte relación negativa
-.70 o superior	La relación negativa muy fuerte

Correlación V de Cramer

Es tan similar como el coeficiente de correlación de Pearson. Se utiliza para calcular la correlación con más de 2×2 filas y columnas. La correlación V de Cramer varía entre 0 y 1. El valor cercano a cero asocia que existe muy poca asociación entre las variables y si es cercano a 1 indica una asociación muy fuerte.

Las «estimaciones brutas» para interpretar la fuerza de las correlaciones utilizando la Correlación V de Cramer:

V de Cramer	estimaciones crudas
.25 o superior	Relación muy fuerte
.15 a .25	Relación fuerte
.11 a .15	relación moderada
.06 a .10	relación débil
.01 a .05	Relación nula o insignificante

Problemas de muestra

Problema 1: Calcular el coeficiente de correlación de la siguiente tabla:

TEMA	EDAD X	NIVEL DE GLUCOSA Y
1	42	98
2	23	68
3	22	73
4	47	79
5	50	88
6	60	82

Solución:

Haz una tabla con los datos dados y agrega tres columnas más de XY, X² e Y².

TEMA EDAD X NIVEL DE GLUCOSA Y XY X² Y²

1 42 98 4116 1764 9604

2 23 68 1564 529 4624

3 22 73 1606 484 5329

4 47 79 3713 2209 6241

5 50 88 4400 2500 7744

6 60 82 4980 3600 6724

∑ 244 488 20379 11086 40266

∑xy = 20379

∑x = 244

∑y = 488

∑x² = 11086

∑y² = 40266

n = 6.

Ponga todos los valores en la fórmula del coeficiente de correlación de Pearson:

$R= \frac{n(∑xy) - (∑x)(∑y)}{\sqrt{[n∑x²-(∑x)²][n∑y²-(∑y)²}}$

R = 6(20379) – (244)(488) / √[6(11086)-(244)²][6(40266)-(488)² ]

R = 3202 / √[6980][3452]

R = 3202/4972.238

R = 0,6439

Muestra que la relación entre las variables de los datos es una fuerte relación positiva.

Problema 2: Calcular el coeficiente de correlación de la siguiente tabla:

TEMA	EDAD X	peso Y
1	40	99
2	25	79
3	22	69
4	54	89

Solución:

Haz una tabla con los datos dados y agrega tres columnas más de XY, X² e Y².

TEMA EDAD X Peso Y XY X² Y²

1 40 99 3960 1600 9801

2 25 79 1975 625 6241

3 22 69 1518 484 4761

4 54 89 4806 2916 7921

∑ 151 336 12259 5625 28724

∑xy = 12258

∑x = 151

∑y = 336

∑x² = 5625

∑y² 28724

norte = 4

Ponga todos los valores en la fórmula del coeficiente de correlación de Pearson:

$R= \frac{n(∑xy) - (∑x)(∑y)}{\sqrt{[n∑x²-(∑x)²][n∑y²-(∑y)²}}$

R = 4(12258) – (151)(336) / √[4(5625)-(151)²][4(28724)-(336)²]

R = -1704 / √[-301][-2000]

R=-1704/775.886

R=-2.1961

Muestra que la relación entre las variables de los datos es una relación negativa muy fuerte.

Problema 3: Calcular el coeficiente de correlación para los siguientes datos:

X = 7,9,14 y Y = 17,19,21

Solución:

Las variables dadas son,

X = 7,9,14

y,

Y = 17,19,21

Para encontrar el coeficiente de correlación de las siguientes variables En primer lugar, se debe construir una tabla de la siguiente manera para obtener los valores requeridos en la fórmula.

X Y XY X² Y²

7 17 119 49 36

9 19 171 81 361

14 21 294 196 441

∑ 30 ∑ 57 ∑ 584 ∑ 326 ∑ 838

∑xy = 584

∑x = 30

∑y = 57

∑x² = 326

∑y² = 838

norte = 3

Ponga todos los valores en la fórmula del coeficiente de correlación de Pearson:

$R= \frac{n(∑xy) - (∑x)(∑y)}{\sqrt{[n∑x²-(∑x)²][n∑y²-(∑y)²}}$

R = 3(584) – (30)(57) / √[3(326)-(30)²][3(838)-(57)²]

R = 42 / √[78][-735]

R = 42/-239,43

R = -0.1754

Se muestra que la relación entre las variables de los datos es una relación despreciable

Problema 4: Calcular el coeficiente de correlación para los siguientes datos:

X = 21, 31, 25, 40, 47, 38 y Y = 70,55,60,78,66,80

Solución:

Las variables dadas son,

X = 21,31,25,40,47,38

Y,

Y = 70,55,60,78,66,80

Para encontrar el coeficiente de correlación de las siguientes variables En primer lugar, se debe construir una tabla de la siguiente manera para obtener los valores requeridos en la fórmula.

X Y XY X² Y²

21 70 1470 441 4900

31 55 1705 961 3025

25 60 1500 625 3600

40 78 3120 1600 6094

47 66 3102 2209 4356

38 80 3040 1444 6400

∑202 ∑409 ∑13937 ∑7280 ∑28265

∑xy = 13937

∑x = 202

∑y = 409

∑x² = 7280

∑y² = 28265

norte = 6

Ponga todos los valores en la fórmula del coeficiente de correlación de Pearson:

$R= \frac{n(∑xy) - (∑x)(∑y)}{\sqrt{[n∑x²-(∑x)²][n∑y²-(∑y)²}}$

R = 6(13937) – (202)(409) / √[6(7280) – (202)²][6(28265) – (409)²]

R = 1004 /√[2876][2909]

R = 1004 / 2892.452938

R = 0,3471

Se muestra que la relación entre las variables de los datos es una relación positiva moderada.

Problema 5: ¿Calcular el coeficiente de correlación para los siguientes datos?

X = 5, 9, 14, 16 y Y = 6, 10, 16, 20.

Solución:

Las variables dadas son,

X = 5 ,9 ,14, 16

Y

Y = 6, 10, 16, 20.

Para encontrar el coeficiente de correlación de las siguientes variables, primero se debe construir una tabla de la siguiente manera, para obtener los valores requeridos en la fórmula, agregue todos los valores en las columnas para obtener los valores utilizados en la fórmula

X Y XY X² Y²

5 6 30 25 36

9 10 90 81 100

14 dieciséis 224 196 256

dieciséis 20 320 256 400

∑44 ∑52 ∑664 ∑558 ∑792

∑xy = 664

∑x = 44

∑y = 52

∑x² = 558

∑y² = 792

norte = 4

Ponga todos los valores en la fórmula del coeficiente de correlación de Pearson:

$R= n(∑xy) - (∑x)(∑y) / √[n∑x²-(∑x)²][n∑y²-(∑y)²$

R = 4(664) – (44)(52) / √[4(558) – (44)²][4(792) – (52)²]

R = 368 / √[296][464]

R = 368/370.599

R = 0,9930

Muestra que la relación entre las variables de los datos es una relación positiva muy fuerte.

Problema 6: Calcular el coeficiente de correlación para los siguientes datos:

X = 10, 13, 15, 17, 19 y Y = 5, 10, 15, 20, 25.

Solución:

Las variables dadas son,

X = 10, 13, 15, 17, 19 y Y = 5, 10, 15, 20, 25.

Para encontrar el coeficiente de correlación de las siguientes variables, primero se debe construir una tabla de la siguiente manera, para obtener los valores requeridos en la fórmula, también agregue todos los valores en las columnas para obtener los valores utilizados en la fórmula,

X Y XY X² Y²

10 5 50 100 25

13 10 130 169 100

15 15 225 225 225

17 20 340 340 400

19 25 475 475 625

∑74 ∑75 ∑1103 ∑1144 ∑1375

∑xy = 1103

∑x = 74

∑y = 75

∑x² = 1144

∑y² = 1375

norte = 5

Ponga todos los valores en la fórmula del coeficiente de correlación de Pearson:

$R= \frac{n(∑xy) - (∑x)(∑y)}{\sqrt{[n∑x²-(∑x)²][n∑y²-(∑y)²}}$

R = 5(1103) – (74)(75) / √ [5(1144) – (74)²][5(1375) – (75)²]

R = -35 / √[244][1250]

R = -35/552,26

R = 0,0633

Muestra que la relación entre las variables de los datos es una relación despreciable.

Problemas 7: Calcular el coeficiente de correlación para los siguientes datos:

X = 12, 10, 42, 27,35,56 y Y = 13, 15, 56, 34,65,26

Solución:

Las variables dadas son,

X = 12, 10, 42, 27, 35, 56 y Y = 13, 15, 56, 34, 65, 26

Para encontrar el coeficiente de correlación de las siguientes variables, primero se debe construir una tabla de la siguiente manera, para obtener los valores requeridos en la fórmula, también agregue todos los valores en las columnas para obtener los valores utilizados en la fórmula.

X Y XY X² Y²

12 13 156 144 169

10 15 150 100 225

42 56 2352 1764 3136

27 34 918 729 1156

35 sesenta y cinco 2275 1225 4225

56 26 1456 3136 676

∑182 ∑209 ∑7307 ∑7098 ∑9587

∑xy = 7307

∑x = 182

∑y = 209

∑x² = 7098

∑y² = 9587

norte = 6

Ponga todos los valores en la fórmula del coeficiente de correlación de Pearson:

$R= \frac{n(∑xy) - (∑x)(∑y)}{\sqrt{[n∑x²-(∑x)²][n∑y²-(∑y)²}}$

R = 6(7307) – (182)(209) / √ {[6(7098) – (182)²][6(9587)-(209)²]}

R = 5804 / √[9464][13841]

R = 5804/11445.139

R = 0,5071

Muestra que la relación entre las variables de los datos es una fuerte relación positiva.

Publicación traducida automáticamente

Artículo escrito por chhabradhanvi y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Coeficiente de correlación Fórmula

Tipos de fórmulas

correlación de Pearson

Coeficiente de correlación lineal

Correlación V de Cramer

Problemas de muestra

Deja una respuesta Cancelar la respuesta