La medición es una rama de la geometría que estudia o mide el área, el perímetro y el volumen de objetos y construcciones bidimensionales o tridimensionales. La medición comprende fórmulas matemáticas fundamentales y, en determinadas circunstancias, expresiones algebraicas.
Rombo
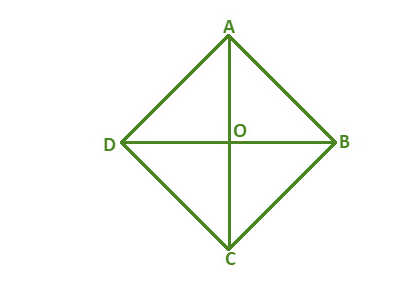
Un rombo es un cuadrilátero en forma de diamante con lados iguales pero ángulos de inclinación desiguales entre estos dos lados. Tiene cuatro lados que tienen la misma longitud ya que es un cuadrilátero.
Rombo
Propiedades de un rombo
- Todos los lados tienen la misma longitud y los lados opuestos son paralelos entre sí.
- Los ángulos adyacentes suman 180°, pero los ángulos opuestos permanecen constantes.
- Las diagonales son perpendiculares entre sí y bisecan los ángulos entre los lados, es decir, los ángulos de los vértices.
- La suma de los ángulos del rombo es 360°.
- Si el ángulo de cada vértice es de 90°, el rombo es un cuadrado.
fórmulas de rombo
Las fórmulas del rombo incluyen la fórmula del área de diferentes maneras que constan de diferentes fórmulas, la fórmula también incluye el perímetro del rombo. Echemos un vistazo a estas fórmulas,
Área de Rombo
El espacio completo cubierto o abarcado por un rombo en un plano bidimensional se define como su área. El área de un rombo se puede calcular usando tres métodos distintos: diagonal, base y altura, y trigonometría.
- I er Caso Usando Diagonal: Es la mitad del producto de las longitudes de las diagonales.

Área del rombo = (d 1 × d 2 )/2 unidades cuadradas
Donde, d 1 es la longitud de la diagonal 1 y d 2 es la longitud de la diagonal 2.
- 2º Caso Usando Base y Altura: La base de un rombo es uno de sus lados, y la altura es la distancia perpendicular desde la base elegida hasta el lado opuesto.

Área de un rombo = base × altura unidades cuadradas
Donde, b es la longitud de cualquier lado del rombo y h es la altura del rombo.
- 3er caso Usando trigonometría
Área del rombo: (lado ) 2 × sin(A) unidades cuadradas
Aquí cuadra el lado del rombo
Y Sin (A) es el ángulo interior.
perímetro de rombo
El perímetro de un rombo es la suma de sus cuatro lados o es el producto de la longitud de un lado por 4.
Por lo tanto, el perímetro de la fórmula del rombo = 4a, donde ‘a’ es el lado.
Perímetro de Rombo = lado + lado + lado + lado = 4s.
- Perímetro de rombo usando longitudes diagonales
Dada una longitud diagonal horizontal de a y una longitud diagonal vertical de b, el perímetro se calcula de la siguiente manera:
PAG = √(un 2 + segundo 2 ) × 2
Ejemplos de preguntas
Pregunta 1: ¿Cuál es el área del rombo para el cual la longitud de las diagonales es de 6 cm, 8 cm.
Solución:
Dadas las longitudes de las diagonales,
Diagonal (D 1 ) = 6 cm
Diagonal (D 2 ) = 8 cm
Usando la fórmula Diagonal: Área del rombo = (d 1 × d 2 )/2 unidades cuadradas
= (1/2) × 6 × 8
= (1/2) × 48
= 24
Entonces el área del rombo es de 24 cm 2 .
Pregunta 2: Calcula el área de un rombo (usando base y altura) si su base es de 6 cm y su altura es de 2 cm.
Solución:
Dado,
Base (b) = 6 cm
altura del rombo(h) = 2 cm
Ahora,
Área del rombo(A) = base × altura
= 6 × 2
= 12cm2
Pregunta 3: Encuentra la diagonal de un rombo si su área es de 120 cm 2 y la longitud de la diagonal más larga es de 12 cm.
Solución:
Dado: Área del rombo = 120 cm 2 y Diagonal d 1 = 12 cm.
Por lo tanto, Área de la fórmula del rombo, A = (d 1 × d 2 )/2 unidades cuadradas, obtenemos
120 = (12 × re 2 )/2
120 = 6 × re 2
O d 2 = 120/6
d 2 = 20
Por lo tanto, la longitud de otra diagonal es de 20 cm.
Pregunta 4: Halla el perímetro de un rombo cuyo lado mide 7 cm.
Solución:
Lado dado s = 7 cm
Por lo tanto, Perímetro de Rombo: 4 × s
Entonces, Perímetro (P) = 4 × 7 cm = 28 cm
Pregunta 5: Encuentra la longitud del lado de un rombo cuyo perímetro es de 60 cm.
Solución:
Perímetro dado (P) = 60 cm
perímetro = 4 × lado
Lado = P/4
Entonces, lado = 60/4
= 15cm
Por lo tanto, la longitud del rombo es de 15 cm.
Pregunta 6: Encuentra el perímetro del rombo dado que las longitudes de las diagonales son 3 cm y 4 cm respectivamente.
Solución:
Cuando las longitudes de las diagonales se dan a = 3 cm, b = 4 cm
Perímetro(P) = 2 × √(a 2 + b 2 )
= 2 × √(3 2 + 4 2 )
= 2 × √(9 + 16)
= 2 × 5
= 10cm
Pregunta 7: Halla el perímetro de un rombo cuyo lado mide 3,5 cm.
Solución:
Dado que el lado s = 3,5 cm
El perímetro de Rombo está dado por: 4 × s
Entonces, Perímetro (P) = 4 × (3.5) cm
= 14 centímetros
Publicación traducida automáticamente
Artículo escrito por Nishant_Singh y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA