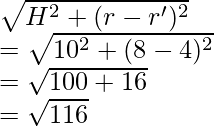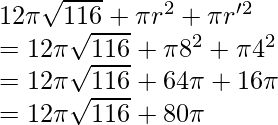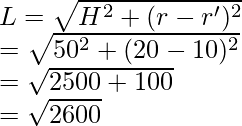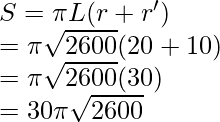Frustum de un cono – Barcelona Geeks

En nuestra vida diaria, nos encontramos con muchos objetos en los que necesitamos encontrar su volumen y áreas de superficie. Por ejemplo, podríamos tener que calcular cuánta agua puede contener un tanque. Para esto, necesitamos saber la forma del tanque y, además, necesitamos saber cómo calcular su volumen. A veces, algunos sólidos son una combinación de diferentes formas estándar.

Frustum of a Cone

La figura de arriba muestra algunas formas sólidas básicas. Los objetos generalmente se componen de una combinación de estas formas. Pero a veces podemos hacer otra forma a partir de un sólido quitando una parte de él. Por ejemplo, Frutum. En esta forma, estamos interesados en eliminar una parte de un cono. Estudiemos el tronco en detalle.

Tronco

Supongamos un cono circular recto y eliminemos una parte de él. Cortemos el cono con un plano paralelo a la base.

Frustum

La forma que queda después de cortar el pequeño cono superior se llama tronco de cono. Todos hemos visto mucho esta forma en nuestra vida diaria, nuestros vasos tienen esta forma. Entonces, el tronco se puede definir como,

Si un cono circular recto es cortado por un plano paralelo a su base, la forma de la porción entre el plano de corte y el plano base se llama tronco de cono.

Veamos el volumen y el área de superficie de esta forma.

Volumen de un Frustum

La definición de tronco de árbol dada anteriormente establece que el tronco de árbol es una parte cortada de un cono. Entonces, para calcular el volumen del tronco, solo necesitamos calcular la diferencia entre el volumen del cono más grande y el más pequeño.

Volume of a Frustum

En la figura dada arriba supongamos,

La altura total del cono será «H + h»
La altura inclinada total debe ser «l1 + l2»
El radio del cono más grande = R
El radio del cono cortado = r

El volumen total del cono V ₁ = $\\ \frac{1}{3}\pi R^2 (H + h)$

El Volumen del cono más pequeño que se quitó V ₂ = $\\ \frac{1}{3}\pi r^2h$

Entonces ahora calculemos el volumen del tronco (V)

V = V ₁ – V ₂

= $\frac{1}{3}\pi R^2 (H + h)$ – $\frac{1}{3}\pi r^2 h$

= $\frac{1}{3} \pi [R^2(H+h) - r^2h]$

Ahora usando la fórmula de la función tangente en trigonometría obtenemos,

$\\ \frac{R}{H+h} = \frac{r}{h} \\ \frac{R}{r} = \frac{H+h}{h} \\ H + h = \frac{Rh}{r}$

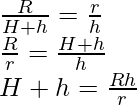
Ingresando este valor de H+h en la fórmula de Volumen.

V = $\\ \frac{1}{3} \pi [R^2(\frac{Rh}{r} - r^2h] \\ = \frac{1}{3}\pi \frac{[R^3h -r^3h]}{r}$

Usando nuevamente la propiedad del triángulo similar, encontraremos el valor de h.

$\\ \frac{R}{H+h} = \frac{r}{h} \\ \frac{R}{r} = \frac{H+h}{h} \\ Rh = Hr + hr \\ h(R - r) = Hr \\ h = \frac{Hr}{R - r}$

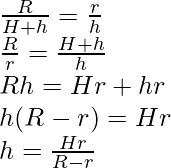
Sustituyendo este valor de h en la fórmula, obtenemos

$\\ V = \frac{1}{3}\pi \frac{[R^3h - r^3h]}{r} \\ = \frac{1}{3} \pi \frac{h(R^3 - r^3)}{r} \\ = \frac{1}{3} \pi \frac{\frac{Hr}{R - r}(R^3 - r^3)}{r} \\ = \frac{1}{3} \pi H(R^2 + r^2 + Rr) \\$

Área de superficie del Frustum

Surface Area of the Frustum

Similar al Volumen, el área de superficie también será igual a la diferencia entre las áreas de superficie del cono más grande y el cono más pequeño.

El área de la superficie curva del cono más grande = π Rl

El área de la superficie curva del cono más pequeño = π rl’

Diferencia entre áreas de superficie = π (Rl – rl’)

En la figura anterior, los triángulos OAB y OCD son similares. Asi que,

$\\ \frac{l'}{l} = \frac{r'}{r} \\ \frac{l - L}{l} = \frac{r'}{r} \\ lr - rL = r'l \\ l(r - r') = rL \\ l = \frac{rL}{r - r'}$

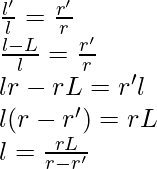
Calculemos las circunferencias de las bases,

C = 2π r y C’ = 2π r’

Entonces, el área total de la superficie curva del tronco A,
$= \\ \frac{1}{2}(Cl - C'l') \\ = \frac{1}{2}(2\pi rl - 2 \pi r'l') \\ = \frac{ 1}{2}(2\pi rl - 2 \pi r'\frac{r'l}{r} \\ = \frac{1}{2}2 \pi l\frac{(r^2 - r '^2)}{r} \\ = \pi l\frac{(r^2 - r'^2)}{r} \\ = \pi L\frac{r}{r - r'}(\ fracción{r^2 - r'^2}{r}) \\ = \pi L(r + r')$

Aquí, L es la altura inclinada dada por, L = $\\ \sqrt{ H^2 + (r - r')^2}$

El área de superficie total del tronco = Área de superficie curva total del tronco A + Área de ambas bases

Veamos algunos problemas relacionados con estas fórmulas que acabamos de derivar.

Problemas de muestra

Pregunta 1: Averigüe el volumen de un tronco de cono que tiene 20 cm de altura y los radios de ambas bases son 5 cm y 8 cm.

Solución:

Usando la fórmula estudiada anteriormente,

$V = \frac{1}{3} \pi H(R^2 + r^2 + Rr) \\$

Nos dan, H = 20 cm, r = 5 cm y R = 8 cm. Introduciendo estos valores en la ecuación.

$V = \frac{1}{3} \pi H(R^2 + r^2 + Rr) \\ = \frac{1}{3} \pi 20(8^2 + 5^2 + (5)(8)) \\ = \frac{1}{3} \pi 20(64 + 25 + 40)) \\ = \frac{1}{3} \pi 20(129) \\ = \frac{1}{3} \pi 258 \\ = 86 \pi \text{ cubic units}$

Pregunta 2: Averigüe el área de superficie y el área de superficie total de un tronco de cono que tiene 10 cm de alto y los radios de ambas bases son de 4 cm y 8 cm.

Solución:

Conocemos la fórmula para el área de superficie y el área de superficie total del tronco. Necesitamos conectar los valores requeridos.

Superficie curvada del tronco = $\pi L(r + r')$

donde L $= \sqrt{ H^2 + (r - r')^2}$

Dado, H = 10 cm, r = 4 cm y r’ = 8 cm

Calculando el valor de L, L = $\sqrt{ H^2 + (r - r')^2} \\ = \sqrt{ 10^2 + (8 - 4)^2} \\ = \sqrt{100 + 16} \\ = \sqrt{116}$

Superficie curvada del tronco = $\pi L(r + r') = \pi \sqrt{116}(8 + 4) \\ = 12 \pi \sqrt{116}$

Área de superficie total = Superficie curvada del tronco + Área de ambas bases

= $\\ 12 \pi \sqrt{116} + \pi r^2 + \pi r'^2 \\ = 12 \pi \sqrt{116} + \pi 8^2 + \pi 4^2 \\ = 12 \pi \sqrt{116} + 64\pi + 16\pi \\ = 12 \pi \sqrt{116} + 80\pi$

Pregunta 3: Digamos que tenemos un cubo de metal abierto cuya altura es de 50 cm y los radios de las bases son de 10 cm y 20 cm. Halla el área de la lámina metálica que se usó para hacer el balde.

sample problem

Solución:

El cubo tiene forma de tronco que se cerró desde el fondo. Necesitamos calcular el área total de la superficie de este tronco.

Dado: H = 50 cm, r ₁ = 10 cm y r ₂ = 20 cm.

Área de superficie curva del tronco S = $\pi L(r + r')$

Primero calculemos L,

$L = \sqrt{ H^2 + (r - r')^2} \\ = \sqrt{50^2 + (20 - 10)^2} \\ = \sqrt{2500 + 100} \\ = \sqrt{2600}$

Poniendo este valor en el área superficial de la fórmula,

$S = \pi L(r + r') \\ = \pi \sqrt{2600} ( 20 + 10) \\ = \pi \sqrt{2600}(30) \\ = 30 \pi \sqrt{2600}$

Esta es la superficie curva. Para encontrar el área total (A) de la hoja de metal utilizada,

A = S + Área del fondo

$\\ = 30 \pi \sqrt{2600} + \pi 10^2 \\ = 30 \pi \sqrt{2600} + 100 \pi \\ = \pi (300\sqrt{26} + 100) \\ = \pi (300(5.1) + 100 ) \\ = \pi (1530 + 100) = \pi (1630) = 3.14 \times 1630 = 5118.2 \text{ sq. cm}$

Pregunta 4: Halla la expresión del volumen de un tronco si su altura es 5y cm, los radios son y y 2y.

Solución:

Usando la fórmula estudiada anteriormente,

$V = \frac{1}{3} \pi H(R^2 + r^2 + Rr) \\$

Nos dan, H = 5y, r = y y R = 2y. Introduciendo estos valores en la ecuación.

$V = \frac{1}{3} \pi H(R^2 + r^2 + Rr) \\ = \frac{1}{3} \pi (5y) ((2y)^2 + y^2 + (2y)(y)) \\ = \frac{1}{3} \pi (5y) (4y^2 + y^2 + 2y^2) \\ = \frac{1}{3} \pi (5y) (7y^2) \\ = \frac{1}{3} \pi 35y^3$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Tronco

Volumen de un Frustum

Área de superficie del Frustum

Problemas de muestra

Deja una respuesta Cancelar la respuesta