Una función es un objeto matemático que asocia cada entrada con exactamente una salida. Por ejemplo: si una función toma cualquier entrada y da como resultado 3. Se puede representar en forma matemática como f(x) = 3. Como otro ejemplo, tomemos f(x) = x 2 , esta función se comporta de la siguiente manera: de la misma manera para todos los valores de su dominio. Pero también puede haber algunas funciones que se comporten de manera diferente para diferentes partes de la entrada.
Por ejemplo: Sea f(x) esa función, digamos si x ∈ (0,3) f(x) = x y para todas las demás x, f(x) = 1.
Esta función se comportó de manera diferente para dos tipos de entrada. Este tipo de funciones se denominan funciones definidas por partes. Vamos a presentarlos más formalmente. La siguiente figura también describe una función por partes. Observe cómo cambia la gráfica de la función para diferentes segmentos de la entrada.

Un ejemplo de una función por partes.
Funciones por partes
Una función por partes es una función que se define en una secuencia de intervalos. Un ejemplo clásico de una función por partes es la función de valor absoluto.
Función de valor absoluto
Tiene dos piezas:
- bajo cero: -x
- de 0 en adelante: x
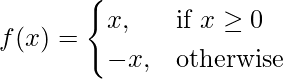

Función de valor absoluto
Evaluar funciones por partes
Pregunta 1: Encuentra el valor de la siguiente función en x = -2,10.
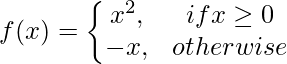
Solución:
en x = -2, x < 0 entonces f(-2) = -2.
en x = 10, x > 0, entonces f(10) = 10 2 = 100.
Pregunta 2: Un juego de arcade cobra los siguientes precios dependiendo del tiempo:
- Hasta 6 minutos cuesta Rs.10
- Más de 6 y hasta 15 minutos cuesta Rs.15
- Más de 15 minutos cuesta Rs.15 más Rs.1 por minuto por encima de 15 minutos
Representa esto como una función por partes y di el precio cobrado si Anil jugó el juego durante 13 minutos y Raju jugó durante 20 minutos.
Solución:
Este tipo de cargos de precios se pueden representar como,
en x = 13, f(13) = Rs.15 y x = 20, f(20 ) = 15 + 1( 20 – 15) = 20.
Función de paso
Estas funciones se utilizan mucho en los campos de la ingeniería eléctrica y electrónica, ya que se utilizan en señales y sistemas. Comencemos con la definición. Es una función por partes con un número finito de partes.
Veamos este gráfico,

La gráfica parece escalera, son una clase de funciones que tienen una gráfica que se parece a una escalera. Dos funciones de paso comúnmente utilizadas son la función de suelo y la función de techo.
Función de piso
La función de suelo, también llamada función de entero mayor o valor entero, da el entero mayor menor o igual que x. El dominio de esta función son todos los números reales R , mientras que el rango de esta función son todos los números enteros I.

Función de piso
Pregunta 1: ¿Cuál es el Piso de 1.43?
Solución:
El piso de un número es el entero mayor menor o igual a ese número. Por lo tanto, aquí el Piso de 1.43 es 1.
Pregunta 2: ¿Cuál es el Piso de -5.66?
Solución:
En el eje Negativo, el Entero mayor menor que -5.66 es -6.
Por lo tanto, -6 es el Piso de -5.66.
Función de techo
Esta función devuelve el entero sucesivo más pequeño. La función techo de un número real x es el menor entero mayor o igual que el número x dado.

Función de techo
Similar a la función suelo, el dominio de la función techo es R y el rango son todos los enteros I.
Pregunta 1: ¿Cuál es el techo de 1,43?
Solución:
El techo de 1,43 debe ser su entero sucesivo más pequeño, por lo que el techo de 1,43 es 2.
Pregunta 2: ¿Cuál es el techo de -7.8?
Solución:
El entero sucesivo más pequeño de -7.8 es -7.
Por lo tanto, -7 es el techo de -7,8.
Función escalón unitario
Este es otro tipo de función que se usa mucho en los estudios de Señales y sistemas. se define como,
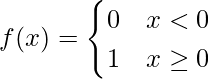
Esta función no tiene valor en x = 0. Se llama función de paso porque en t = 0, da un paso de 0 a 1. El dominio de esta función es R – {0} y el rango {0,1} .

Función escalón unitario
Pregunta 1: ¿Cuál es el piso de 2.31?
Solución:
Dado que la función de piso genera el entero más pequeño más cercano. piso (2.31) = 2.
Pregunta 2: ¿Cuál es el valor máximo de -4,16?
Solución:
Dado que la función de techo devuelve el entero sucesivo más pequeño, ceil(-4.16) = -4.
Pregunta 3: ¿Qué es Piso y techo de 7?
Solución:
En este caso, tanto el suelo como el techo de 7 es el mismo 7 , ya que es el entero más grande menor o igual que 7, así como el entero sucesivo más pequeño de 7.
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA



